leetcode - 学习计划之数据结构入门

73. 矩阵置零

 力扣，给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。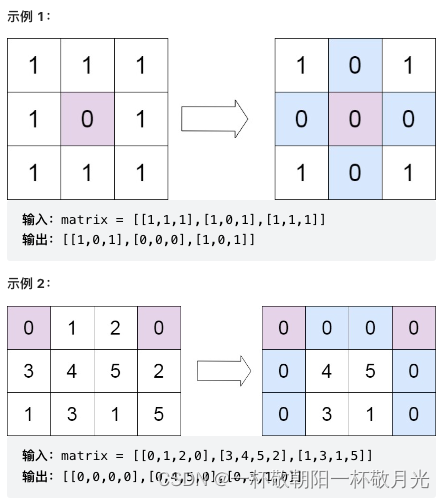

 

题解

一：用两个数组分别记录行和列是否有零，空间复杂度O(m+n)，时间复杂度O(m*n)。

class Solution(object):
    def setZeroes(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.
        """
        m, n = len(matrix), len(matrix[0])
        rows = [False] * m 
        cols = [False] * n 
 
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    rows[i] = True 
                    cols[j] = True 
        
        for i in range(m):
            for j in range(n):
                if rows[i] or cols[j]:
                    matrix[i][j] = 0
        return None

二、将空间复杂度将为O(1)，用第一行来记录对应列中是否有0，若有第一行对应列记0（反正最后也是要变成0的，此处值的先改变不影响），用第一列来记录对应行中是否有0，若有第一列对应行记为0。只不过这样我们就改变了第一行和第一列的值，我们无法标记第一行是否有0，第一列是否有0，所以先用两个变量做个标记。第二次便利，若第一行或第一列对应位置有0，则该位置为0，最后按两个标记处理第一行和第一列。

class Solution(object):
    def setZeroes(self, matrix):
        m, n = len(matrix), len(matrix[0])
        # 用来记录第一行和第一列是否有0的标记
        row_flags = any([matrix[i][0]==0 for i in range(m)])
        col_flags = any([matrix[0][j]==0 for j in range(n)])
 
        for i in range(1, m):
            for j in range(1, n):
                # 其他位置有0，用第一行和第一列标记
                if matrix[i][j] == 0:
                    matrix[i][0] = 0 
                    matrix[0][j] = 0
        
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0
 
        if row_flags:
            for i in range(m):
                matrix[i][0] = 0 
        if col_flags:
            for j in range(n):
                matrix[0][j] = 0
        return None