YOLO V1学习笔记

YOLO V1

• 是一个经典的one-stage方法

• “只看一次”，一个网络架构直接得出结果，速度非常快

• 把检测问题转化为回归问题，一个CNN就搞定了

• 可以对视频进行实时检测，应用领域非常广

1. 基本网络架构：

此处比较难理解的就是将图片划分为7*7*30，7*7比较容易理解，即：将图片划分为7*7的格子，也就是最终网格的大小。对于每一个物体（格子）来说，需要产生两种候选框，而这每一个格子中包含30个值，这30个值被分成了3份，如图上的绿色长条所示，前面的两个5位分别为第一个候选框（b1：宽<高的黄色框）和第二个候选框（b2：宽>高的黄色框）的相关信息，这5位由以下内容组成：

• x，y:
  • 并不是实际的像素点的坐标值，而是被归一化之后的处于0-1之间的一个值
• w，h:
  • 并不是实际的像素点数量值，而是被归一化之后的处于0-1之间的一个值
• c:
  • 置信度值

还剩余20位为20分类，但这个分类是依据数据集来确定的，并不一定每个数据集都是20分类，此处是以20为例，这个20位也就是一个分类任务，每一个位中存放相应类别的置信度值，如下所示：

所以，我们最终需要的就是7*7*30中的这个7和30。

参数的含义总结：

• 10 = （x,y,w,h,c）* Box数量
• 20：当前数据集共有20个类别
• 7*7：表示最终网格的大小
• （S*S）* (Box数量 * 5 + c):表示最终得到的结果

2. 损失函数

   具体组成结构如下图所示：

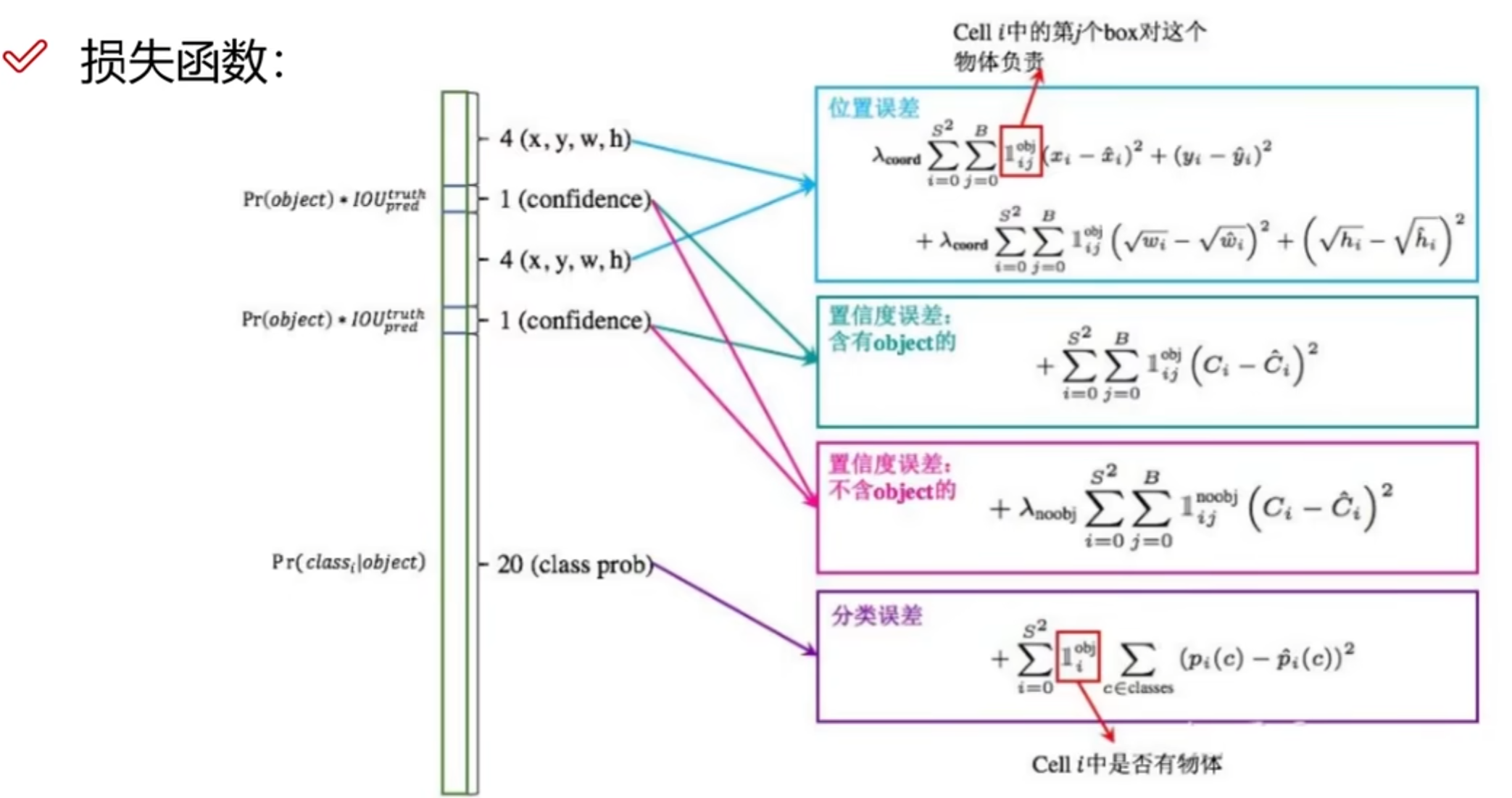
损失函数的作用：由于我们最终得到的结果是30个值的预测值，而我们所希望的是将这些预测值尽可能的趋近真实值，也就是最小化预测值和真实值之间的误差。

1. 位置误差：

   

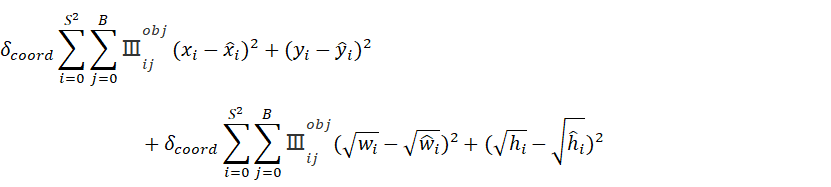
   这里的
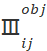
   表示cell i 中的第j个box对这个物体负责，也就是候选框中IOU最大的那个box。对于w和h为什么计算的时候要带根号，可以从函数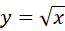
   这个函数的图像得出，当x较小的时候，y的斜率较大，对x的变化较为敏感，当x较大的时候，y的斜率较小，此时对x的变化变得不太敏感，这种情况映射到w和h上时就表现为：当真实框和预测框的w和h都比较大时，那么预测框相对于真实框微小偏移对预测的结果来说则影响不大，而当真实框和预测框的w和h都比较小时，那么预测框相对于真实框微小偏移则会对预测的结果产生相当大的影响。

2. 置信度误差（含object（物体）的）：

   

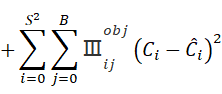
   含有所预测物体的框可以认为是前景框，这时候需要找一个IOU最大的框作为候选框。

3. 置信度误差（不含object（物体）的）：

   

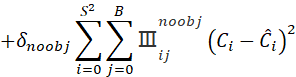
   由于在预测的时候很多框是不含有物体的，这一部分为背景区域。为了避免这一大部分的背景框对结果造成较大影响，所以需要给这一部分值一个权重，使其在相同值条件下对结果的影响程度低于含有object的框。

4. 分类误差：

   用于判断物体是哪种类别

   

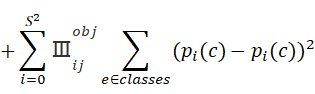
   计算预测物体的概率和真实值之间的概率的交叉熵，交叉熵如何计算？

   在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为 p 和 1−p ，此时表达式为（log 的底数是 e）：
   $$L=\frac{1}{N}\sum _{n=1}{L}_i=\frac{1}{N}\sum _i-[y_i\ast \log (p_i)+(1-y_i)\ast log(1-p_i)]$$
   其中：
   y i : 表示样本 i 的 l a b e l ，正类为 1 ，负类为 0 p i : 表示样本 i 预测为正类的概率

   yi:表示样本i的label，正类为1，负类为0pi:表示样本i预测为正类的概率" role="presentation" style="position: relative;">yi:表示样本i的label，正类为1，负类为0pi:表示样本i预测为正类的概率$$\begin{array}{rl}& y_i:表示样本i的label，正类为1，负类为0\\ & p_i:表示样本i预测为正类的概率\end{array}$$
   ​yi​:表示样本i的label，正类为1，负类为0pi​:表示样本i预测为正类的概率​
   多分类的情况实际上就是对二分类的扩展：
   $$L=\frac{1}{N}\sum _i{L}_i=-\frac{1}{N}\sum _i\sum _{c=1}^M{y}_{ic}log(p_{ic})$$
   其中：
   M : 类别的数量 y i c : 符号函数（ 0 或 1 ），如果样本 i 的真实类别等于 c 取 1 ，否则取 0 p i c : 观测样本 i 属于类别 c 的预测概率
   M:类别的数量yic:符号函数（0或1），如果样本i的真实类别等于c取1，否则取0pic:观测样本i属于类别c的预测概率" role="presentation" style="position: relative;">M:类别的数量yic:符号函数（0或1），如果样本i的真实类别等于c取1，否则取0pic:观测样本i属于类别c的预测概率$$\begin{array}{rl}& M:类别的数量\\ & y_{ic}:符号函数（0或1），如果样本i的真实类别等于c取1，否则取0\\ & p_{ic}:观测样本i属于类别c的预测概率\end{array}$$
   ​M:类别的数量yic​:符号函数（0或1），如果样本i的真实类别等于c取1，否则取0pic​:观测样本i属于类别c的预测概率​

5. NMS（非极大值抑制）：

   顾名思义，非极大值抑制就是排除掉不是极大值的值。实际情况就是，在测试的时候，可能会检测到很多个框都是重叠的，这个时候可以用非极大值抑制去处理

   

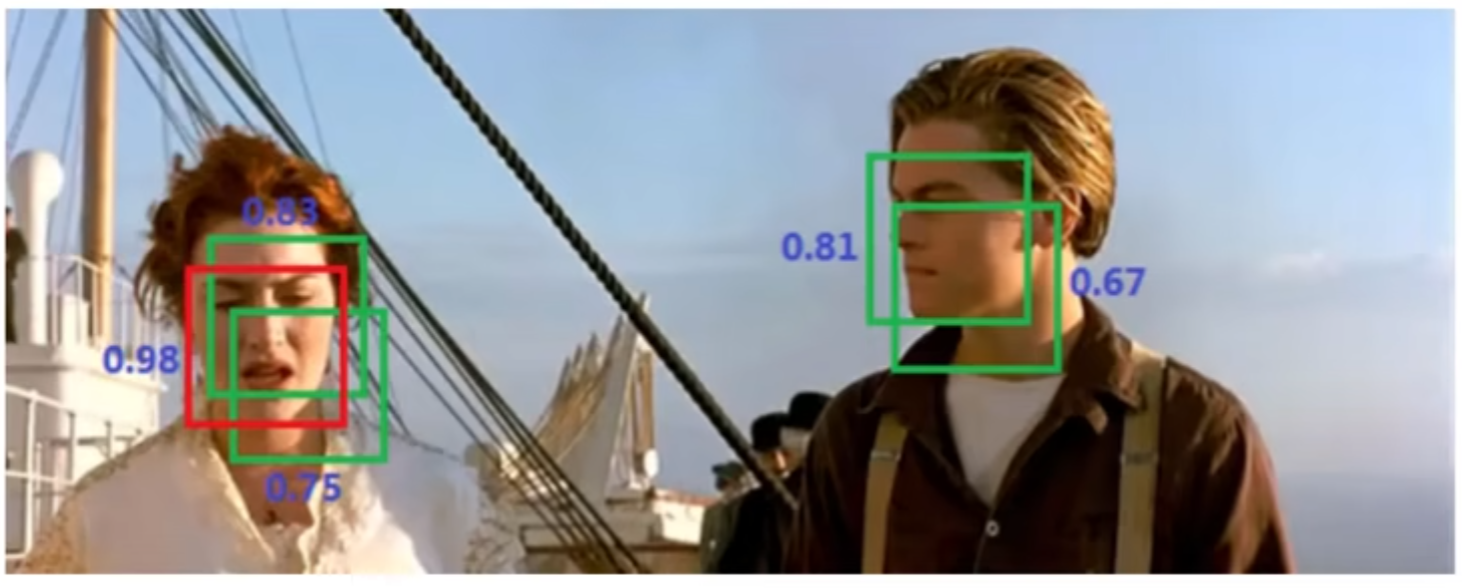
   比如这张图片在识别人脸，并且每个人脸上有多个框，这个时候就需要用非极大值抑制，左侧女性人脸取极大值0.98，右侧男性人脸取极大值0.81

6. YOLO V1

   • 优点：快速，简单
   • 问题1：每个cell只预测一个类别，如果重叠则无法解决
   • 问题2：小物体检测效果一般，长宽比可选但单一