JAVA基础算法（6）----- 国际象棋 α 皇后问题

​
​

国际象棋 α 皇后问题

活动地址：CSDN21天学习挑战赛

一、题目

标题：国际象棋 α 皇后问题

在 α × α 格的国际象棋上摆放 α 个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

二、解题

2.1 思路分析

1. 将第一个皇后放在第一行第一列的格子中；
2. 将第二个皇后放置在第二行第一列的格子中，然后进行判断，如果两个皇后满足不在同一行或同一列以及同一根斜线上的条件，则代表当前位置的格子可以放置一个皇后，这时即可再去寻找第三个皇后的位置，如果两个皇后所处位置不满足条件，那么皇后的列数就要后移一位继续判断，还不满足就再次后移直至满足条件或者证明当前行无法满足条件为止；
3. 当第一个至第 α 个皇后都已经放置好位置时（即 α 个皇后的位置皆不冲突时）就表示当前情况是皇后问题的一种摆法；
4. 得到了一个正确的解后，将其记录并开始回溯到上一个皇后的位置找另外的解法，如果找到了就再次寻找下一个皇后可放置的位置，如果找不到则再退回一层 …… ……；
5. 当第一个皇后放在第一行第一列的情况全部找到后就对第一行第二列 、第三列 、……、第 α 列的情况进行寻找，直至找到所有可能；

2.2

• 进入写代码阶段，第一步我们先创建一个数组用于保存皇后的位置，定义一个变量保存行列数，定义一个变量保存方案数；

（这里可能会有人不明白为什么是建立一个一维数组而不是二维数组，原因很简单，因为皇后的数量是跟行列数为一比一的关系，也就是说每一行都只能有一个皇后，使用一维数组保存的是皇后所处位置的列下标，而每个一维数组的下标则可以表示为皇后的行下标）

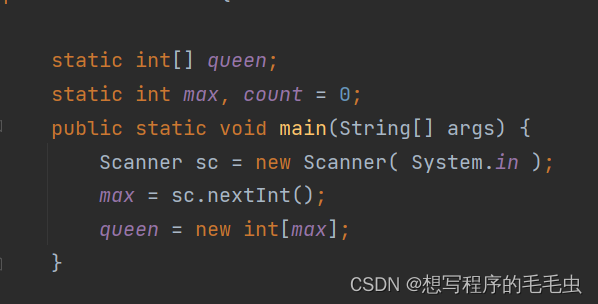
图 2.1

2.3

编写一个方法将初始为 0 的坐标数传入该方法；

图 2.2

2.4

编写方法遍历每一个位置，假定其为皇后正确坐标并由此进入递归计算下一行皇后的位置；

图 2.3

2.5

• 在进入下一个坐标的递归之前，增加一个方法对当前坐标是否符合条件的判断，如果符合则进入递归寻找下一个行皇后的位置，如果不符合则继续遍历下一个列坐标；

• 对坐标是否合法的判断很简单，无非是判断是否和前面所有的皇后处于同一行或同一列以及同一斜线；

• 因为我们只让每一行存在一个皇后，故不需要判断是否存在同一行的情况；

• 因为我们设置的数组是存放皇后的列坐标，所以需要遍历一遍查找是否有相同的情况，如果有代表发生冲突返回 false ，反之则继续下一轮的判断（要跟所有的皇后都没冲突才能返回 true）；

• 此外还要判断是否在同一条斜线上，因为同一对角线上的两个元素，它们的行坐标之差等于列坐标之差，所以我们可以把皇后位置的行坐标（皇后的行坐标就是在当前数组的位置）相减求得差值再与列坐标（皇后的列坐标就是存储的数值）的差值进行比较，如果相等则代表有冲突需要返回 false ，反之则进行下一轮判断；（因为计算机计算差值的时候并不一定会用大数减去小数，故要取绝对值）

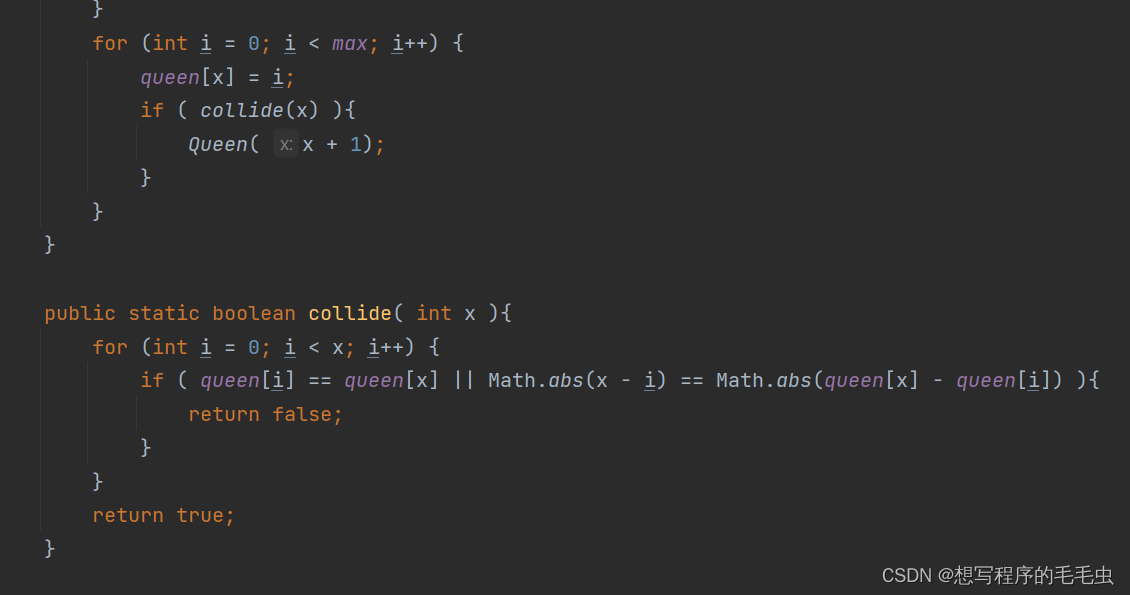
图 2.4

2.6

在寻找皇后列下标的方法内增加一个判断，用于判断是否已经找完所有的皇后的列下标，如果找到了所有的皇后位置就将计数器进行自增记录摆法数，然后再通过返回进行回溯寻找另外的方法；如果判断并未找到所有的皇后位置则再次进入遍历；

图 2.5

2.7

最后在主方法输出方案数即完成了该题；

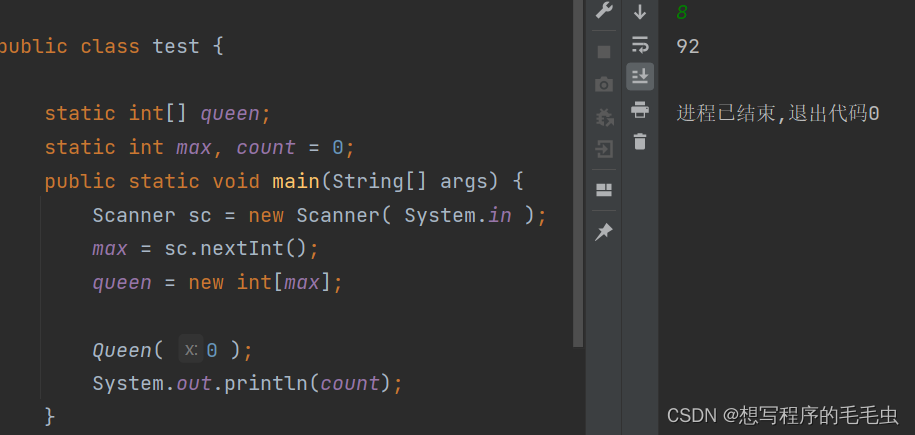
图 2.6

2.8

最后补充一个检查方法，该检查方法就是在每一次得到解决方案的时候将其打印出来；

1. 打印的时候为了更加直观需要建立一个二维数组；
2. 然后将每一行的皇后位置标记为 1 ；（之前有提过 queen 数组存储的是列坐标）
3. 再通过枚举将该数组打印出来；

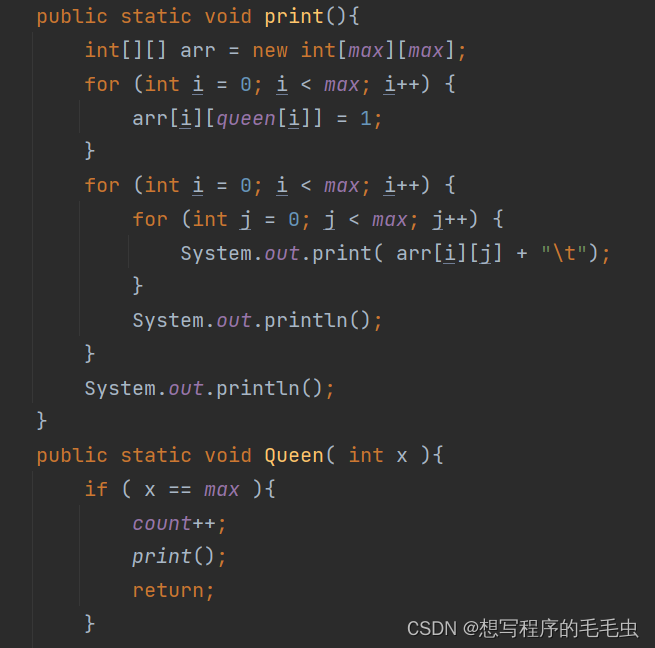
图 2.7

2.9

为避免方阵太多影响视觉，这里就只打印一个 4 x 4 的情况展示；

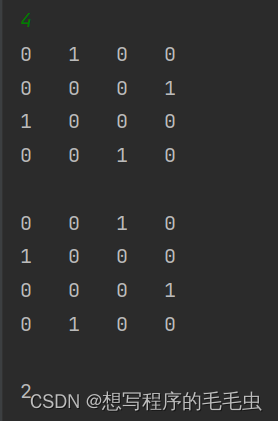
图 2.8

三、代码分享

import java.util.Scanner;

public class test {

    static int[] queen;
    static int max, count = 0;
    public static void main(String[] args) {
        Scanner sc = new Scanner( System.in );
        max = sc.nextInt();
        queen = new int[max];

        Queen( 0 );
        System.out.println(count);
    }
    
    //打印方法
    public static void print(){
        int[][] arr = new int[max][max];
        for (int i = 0; i < max; i++) {
            arr[i][queen[i]] = 1;
        }
        for (int i = 0; i < max; i++) {
            for (int j = 0; j < max; j++) {
                System.out.print( arr[i][j] + "\t");
            }
            System.out.println();
        }
        System.out.println();
    }
    
    //寻找列坐标的方法
    public static void Queen( int x ){
        if ( x == max ){
            count++;
            print();
            return;
        }
        for (int i = 0; i < max; i++) {
            queen[x] = i;
            if ( collide(x) ){
                Queen( x + 1);
            }
        }
    }

    //检查是否存在冲突的方法
    public static boolean collide( int x ){
        for (int i = 0; i < x; i++) {
            if ( queen[i] == queen[x] || Math.abs(x - i) == Math.abs(queen[x] - queen[i]) ){
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55