LeetCode中等题之旋转图像

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

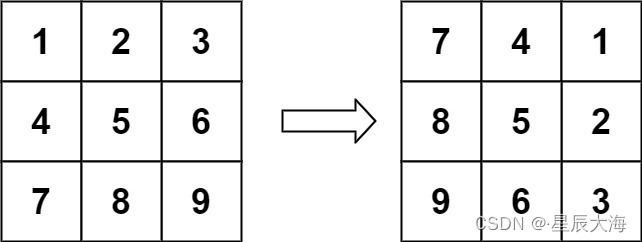
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

来源：力扣（LeetCode）

解题思路

  这种矩阵变换类的题目，如果是方阵难度将会大大降低，针对题目中所给的限制条件，可以考虑用镜像操作代替旋转，这也是常用的等效操，所以可以先上下翻转然后再按主对角线反转。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n=len(matrix)
        for i in range(n//2):
            matrix[i],matrix[n-i-1]=matrix[n-i-1],matrix[i]
        for i in range(n):
            for j in range(i+1):
                matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
1
2
3
4
5
6
7
8
9
10
11