-
优秀论文以及思路分析02
题目:汽车产业是国民经济的重要支柱产业,而新能源汽车产业是战略性新兴产业。大力 发展以电动汽车为代表的新能源汽车是解决能源环境问题的有效途径,市场前景广阔。 但是,电动汽车毕竟是一个新兴的事物,与传统汽车相比,消费者在一些领域,如电池 问题,还是存在着一些疑虑,其市场销售需要科学决策。 某汽车公司最新推出了三款品牌电动汽车,包括合资品牌(用 1 表示)、自主品牌 (用 2 表示)和新势力品牌(用 3 表示)。为研究消费者对电动汽车的购买意愿,制定 相应的销售策略,销售部门邀请了 1964 位目标客户对三款品牌电动汽车进行体验。具 体体验数据有电池技术性能(电池耐用和充电方便)满意度得分(满分 100 分,下同) a1、舒适性(环保与空间座椅)整体表现满意度得分 a2、经济性(耗能与保值率)整体 满意度得分 a3、安全性表现(刹车和行车视野)整体满意度得分 a4、动力性表现(爬 坡和加速)整体满意度得分 a5、驾驶操控性表现(转弯和高速的稳定性)整体满意度得 分 a6、外观内饰整体表现满意度得分 a7、配置与质量品质整体满意度得分 a8 等。另外 还有目标客户体验者个人特征的信息,详情见附录 1 和 2。
问题一
问题:请做数据清洗工作,指出异常值和缺失数据以及处理方法。对数据做描述性统计分析,包括目标客户对于不同品牌汽车满意度的比较分析。
rm(list=ls()) setwd("C:/Users/59956/Desktop/Model") library(openxlsx) library(mice) library(dplyr)- 1
- 2
- 3
- 4
- 5
导入一些库。。。
一、特征转换
特征转换是基于现有的特征,通过进行变换,得到新的特征,从而使得变换后的特征更加有利于数据分析或更加直观。在特征 B8 中,展示了客户体验者的出生年份。由于出生年份这一特征不够直观,本文对这一特征进行了转换,通过使用当前年份与该特征的取值作差,就得到了“年龄”这一新的特征。
二、异常值处理
【1】基于箱线图的潜在异常值检测
当数据当中存在异常值时,尤其是存在着偏离较大的离群点时,会对数据分析和建模带来误差,因此,需要对异常值进行检测。常用的异常值检测方法包括 3σ 法则或 Z分布方法,而这一类方法是以正态分布为假设前提的。由于本文的一部分数值型特征的分布并不符合正态分布,即数据分布不均匀。故本文选择使用对数据分布没有要求的箱
线图,对数值型特性进行异常值检测。使用箱线图对数据进行异常值检测的原理为:通过计算四分位数加减 1.5 倍四分位距,即是计算 Q1-1.5IQR 和 Q3+1.5IQR 的值,规定落在这一区间之外的数据为异常点。在箱线图中,可以看出变量数据的中位数、上四分位数、下四分位数、上下边缘和潜在异常点[3]。本文通过使用上四分位数代替数值大于 Q3+1.5IQR 的数据,使用下四分位数代替数值小于 Q1-1.5IQR 的数据,并绘制出了异常值处理前后的箱线图,如图 1 所示。
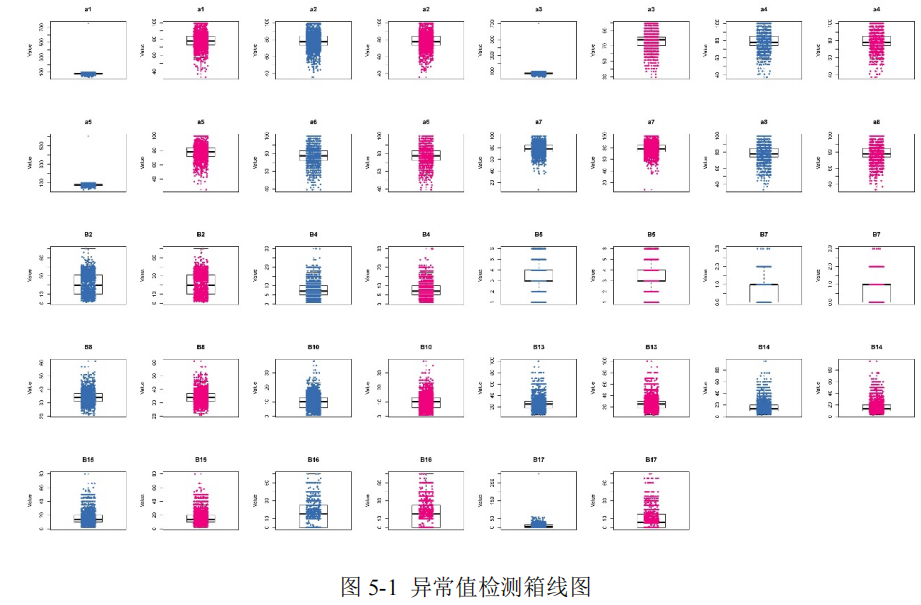
在图 5-1 中,中间部分的线表示中位数,箱子的上下边缘分别表示上四分位数和下四分位数,图中上方和下方的两条横线表示上下边缘,最上方和最下方的点即是潜在离群值。从图中可以看出,一部分特征在异常值处理之后箱线图变化明显,如:a1、a3、a5、B17 等,说明在进行异常值处理之后,这些特征的分布更加的集中,更有利于建模。此外,一些特征并没有检测出异常值,如:B2、B5、B7、B16,说明这些特征原本的数据质量较好。
【2】异常值识别与处理
通过对异常值进行分析我们发现,少量特征存在着个别数值较大的异常值,这些异常值与中位数的数值差距较大。在原数据中,我们经过观察、比较、分析之后发现,一部分异常值是人为导致的。其原因在于:这部分异常值为三位数,超出了满意度得分的满分 100 分这个最大值。同时,这样一些三位数的异常值的小数点后为 7 位,而正常的两位数的小数点后取值为 8 位。因此,我们判断出误差来源于小数点错位。对此,本文对这些异常值进行了更正处理,通过移动小数点,将三位数的异常值更正为两位数。与此同时,对于 B16 和 B17 两个特征,由于是占家庭总收入的比例,故百分号前面的数字应小于 100,而在 B17 中,存在着 300 这一数字,显著大于阈值 100,故我们诊断其为异常值,并对其所在的行进行了删除处理。
#加载所有常用模块 from pyforest import * import warnings warnings.filterwarnings('ignore') data=pd.read_csv("F:/data/null.csv",encoding='gbk') data.head() data.shape import missingno as msno # 可视化看下缺省值 msno.matrix(data, labels = True) msno.bar(data)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
【3】缺失值处理
本文针对附录一中的目标客户体验数据,首先利用 Python 软件查找出不同特征下的缺失值分布情况,如图 5-2 所示。从图 5-2 可以看出,缺失值仅存在于 B7(孩子数量)这一特征中,且缺失值在数据集中的不同行的分布较为均匀,说明这些缺失值是随机缺失的。

结合图 5-3,统计出 B7 所在列的缺失值个数为 500。本文进一步探究缺失值所在观测的内在联系,结合问卷的信息,可以明确目标用户的 B6(婚姻家庭情况)的取值,会限制 B7 的取值范围。
这里插一句:比赛当中有一份关于数据的问卷调查,感兴趣的同学自己b站找找。。。

利用表 5-1 及 B7 的取值公式,本文将 B6 取值为 1,2,3,4 或 8,对应的 B7 列的缺失值填补为 0。并对于 B6 取值为 5 或 7 的情形,本文假定在 B6 真实的情况下,按照 B7列非缺失的数据的中位数 1,作为在 B6 取值为 5 或 7 的缺失值取值。【4】描述性统计分析
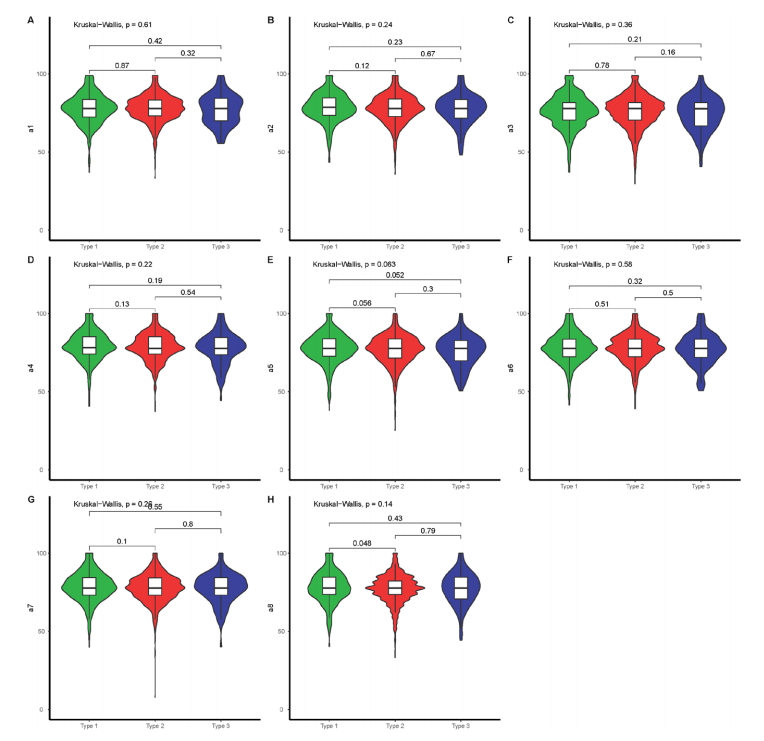
这里使用的是小提琴图,即绘制出三个品牌关于 8 个满意度变量的小提琴图。
他们还针对”居住区域”这一分类特征进行描述性统计分析。##树形图 \python3.0 import squarify #分类变量可视化 data=pd.read_csv("F:/data/B3.csv",encoding='gbk') data.head() #图片显示中文 plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus'] =False #减号 unicode 编码 df = data.groupby('居住区域').size().reset_index(name='counts') labels = df.apply(lambda x: str(x[0]) + "\n (" + str(x[1]) + ")", axis=1) sizes = df['counts'].values.tolist() colors = [plt.cm.Spectral(i/float(len(labels))) for i in range(len(labels))] # Draw Plot plt.figure(figsize=(12,8), dpi= 80) squarify.plot(sizes=sizes, label=labels, color=colors, alpha=.8) # Decorate plt.title('目标客户居住区域分布情况') plt.axis('off') plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19

问题二
问题:决定目标客户是否购买电动车的影响因素有很多,有电动汽车本身的因素,也有目标客户个人特征的因素。在这次目标客户体验活动中,有部分目标客户购买了体验的电动汽车(购买了用 1 表示,没有购买用 0 表示)。结合这些信息,请研究哪些因素可能会对不同品牌电动汽车的销售有影响?
一、数据归一化
为消除数据量纲的影响,需要对数值型变量进行最大最小归一化,将数据转化为 0 至 1 之间的数值。由于分类型变量在 One-Hot 编码后的取值只有 0 和 1,因此分类型变量无需进行归一化。
二、ADASYN 采样
在附录 1 的所有数据样本中,有购买意愿的顾客数为 99,占比 5%,数据极度不平
衡。如果直接用不平衡的样本筛选特征,会导致特征无法很好地预测少数类的样本;如
果用不平衡的样本建立模型,会导致极高的正确率和极低的泛化能力。因此,本文对不
同品牌的客户数据分别进行了采样处理。考虑到标签为“1”的样本数量较少,本文使用
ADASYN 上采样的方法,通过扩大少数类样本的数量,对训练集进行采样处理。本文分别对三种汽车品牌的 7 个分类变量与“购买意愿”这一目标变量分别进行卡方检验,并计算出卡方检验结果的得分和P 值。通过设置得分阈值为 S,得到了大于阈值的 N1 个变量。值得注意的是,由于本文的特征筛选由多个步骤组成,因此此处通过人为设定阈值并不会对最终的特征集造成影响,因为如果存在少量不合理的特征,在后续的特征筛选中也会被过滤掉。
三、分类型特征筛选
【1】基于卡方检验的分类型特征初筛
##卡方检验 \python3.0 data=pd.read_csv("F:/data/category3.csv",encoding='gbk') data.head() data.shape import matplotlib.pyplot as plt#加载所有常用模块 from pyforest import * import warnings warnings.filterwarnings('ignore') import numpy as np import pandas as pd X=data.drop(['label'], axis=1) #删除列 y=data['label'] from imblearn.over_sampling import ADASYN X_resampled, y_resampled = ADASYN().fit_sample(X, y) print('采样结果为:') print(y_resampled.value_counts()) from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 model1 = SelectKBest(chi2,k=4)#选择 k 个最佳特征 model1.fit_transform(X_resampled, y_resampled) #该函数可以选择出 k 个特征 model1.scores_ #得分 model1.pvalues_ #p-values d = pd.DataFrame(model1.scores_) #转为 dataframe d.to_csv("F:/data/chi.csv",index=False)#转换成 csv 文件- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
他们分别对三种汽车品牌的 7 个分类变量与“购买意愿”这一目标变量分别进行卡方检验,并计算出卡方检验结果的得分和P 值。通过设置得分阈值为 S,得到了大于阈值的 N1 个变量。值得注意的是,由于特征筛选由多个步骤组成,因此此处通过人为设定阈值并不会对最终的特征集造成影响,因为如果存在少量不合理的特征,在后续的特征筛选中也会被过滤掉。

【2】基于最大信息系数法的分类型特征二次筛选
在前面筛选得到 4 个分类型变量的基础上,使用最大信息系数法对分类变量进行二次筛选。

##9. 最大信息系数法 \python3.0 import numpy as np from sklearn.feature_selection import SelectKBest from minepy import MINE data=pd.read_csv("F:/data/info3.csv",encoding='gbk') data.head() data.shape a=data.drop(['label'], axis=1) #删除列 b=data['label'] from imblearn.over_sampling import ADASYN X_resampled, y_resampled = ADASYN().fit_sample(a, b) print('采样结果为:') print(y_resampled.value_counts()) #由于 MINE 的设计不是函数式的,定义 mic 方法将其为函数式的,返回一个二元组,二元组的第 2 项设置成固定的 P 值 0.5 def mic(x, y): m = MINE() m.compute_score(x, y) return (m.mic(), 0.5) #由于 MINE 的设计不是函数式的,定义 mic 方法将其为函数式的,返回一个二元组,二元组的第 2 项设置成固定的 P 值 0.5 def mic(x, y): m = MINE() m.compute_score(x, y) return (m.mic(), 0.5) #选择 K 个最好的特征,返回特征选择后的数据 new=SelectKBest( lambda X, Y: np.array(list(map(lambda x: mic(x, Y), X.T))).T[0], k=2).fit_transform(X_resampled, y_resampled) new- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
四、数值型特征筛选
【1】基于方差过滤法的数值型特征初筛

##10. 方差过滤法 \python3.0 data=pd.read_csv("F:/data/num1.csv",encoding='gbk') data.head() data=data.drop(['label'], axis=1) #删除列 data.shape data.describe() des1 = data.describe() std1 = des1.loc['std'].sort_values(ascending=False) X_16_1 = data[std1[std1>0.14].index] #设置方差阈值=0.1 X_16_1.shape X_16_1.to_csv("F:/data/var.csv",index=True,encoding='gbk')#转换成 csv 文件- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
【2】基于随机森林的数值型特征二次筛选
在前面筛选出的 13 个候选指标中,通过随机森林度量各特征的重要性程度。
这里以品牌 1 为例,将特征按重要性程度从高到低进行排序后,绘制出特征重要性程度图,如 6-1 所示。
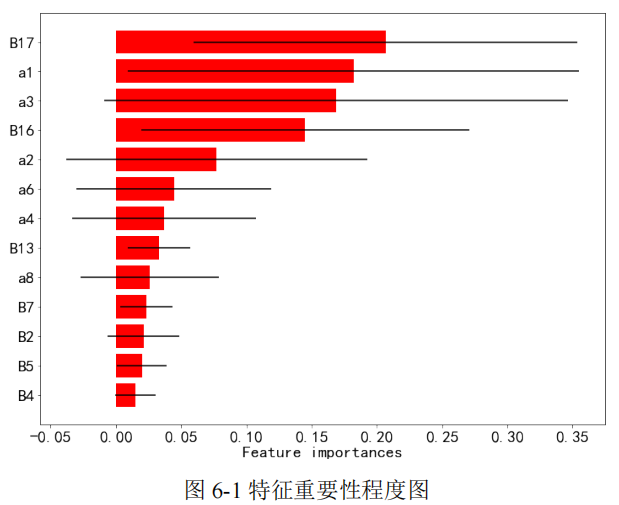
本文通过删除重要性程度排序最靠后的 5 个特征,得到了三种品牌的数值特征二次
筛选后的特征集。
##11. 随机森林度量特征重要性 \python3.0 from sklearn.ensemble import RandomForestClassifier import matplotlib.pyplot as plt from sklearn.feature_selection import SelectFromModel data=pd.read_csv("F:/data/ran3.csv",encoding='gbk') data.head() data.shape X=data.drop(['label'], axis=1) #删除列 y=data['label'] #采样 from imblearn.over_sampling import ADASYN X_resampled, y_resampled = ADASYN().fit_sample(X, y) print('采样结果为:') print(y_resampled.value_counts()) #基于随机森林度量各个变量的重要性 clf = RandomForestClassifier() clf = clf.fit(X_resampled, y_resampled) clf importance1 = np.mean([tree.feature_importances_ for tree in clf.estimators_], axis=0) std1 = np.std([tree.feature_importances_ for tree in clf.estimators_], axis=0) indices = np.argsort(-importance1) # 返回由大到小的数据之前的索引 indices choose_num = 13 # 选择前 13 个因子 suoyin = indices[0:choose_num][::-1] range_ = range(choose_num) columns=X.columns #查看列名 feature_name = pd.Series(columns) feature_name[suoyin] #图片显示中文 plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus'] =False #减号 unicode 编码 ##画图 plt.figure(figsize=(12, 9)) plt.barh(range_, importance1[suoyin], color='r', xerr=std1[suoyin], alpha=1, align='center') plt.xticks(fontsize=20) plt.yticks(range(choose_num), feature_name[suoyin],fontsize=20) plt.ylim([-1, choose_num]) # plt.xlim([0.0,0.055]) plt.xlabel('Feature importances',fontsize=20) plt.show() sum(importance1[suoyin])- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
【3】基于 RFE 递归特征消除的数值型特征三次筛选
由于前面使用随机森林筛选出的特征结果并不是绝对稳定的,该方法由于随机种子设定的不同,筛选出的特征也不全相同。为了使最终建模的特征更加稳定客观,使用递归特征消除的方法对数值型特征进行第三次筛选。

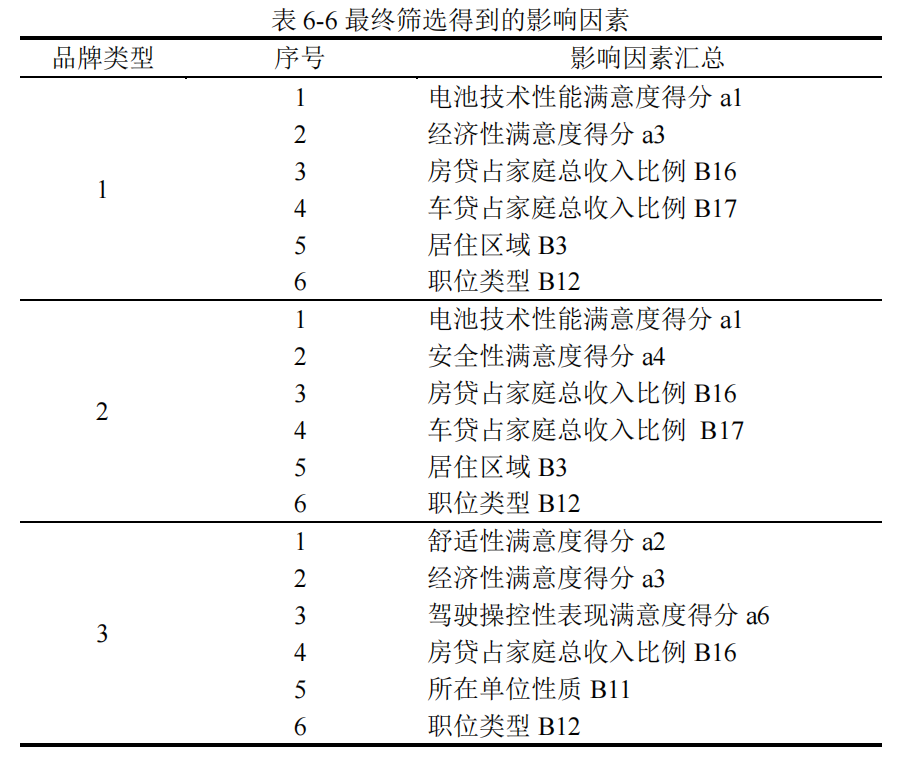
最终分别为三种品牌确定出6个特征,即电动汽车购买的影响因素,用于后面的建模:
##12. RBF 递归特征消除 \python3.0 data=pd.read_csv("F:/data/tree3.csv",encoding='gbk') data.head() X = data.drop(['label'],axis=1) #从数据集中删除目标变量 y = data["label"] #采样 from imblearn.over_sampling import ADASYN X_resampled, y_resampled = ADASYN().fit_sample(X, y) print('采样结果为:') print(y_resampled.value_counts()) from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression #递归特征消除法,返回特征选择后的数据 #参数 estimator 为基模型 #参数 n_features_to_select 为选择的特征个数 rfe=RFE(estimator=GradientBoostingClassifier()).fit_transform(X_resampled, y_resampled) da = pd.DataFrame(rfe) #转为 dataframe da.head() da.to_csv("F:/data/RBF.csv",index=False)#转换成 csv 文件- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
问题三
问题:结合前面的研究成果,请你建立不同品牌电动汽车的客户挖掘模型,并评价模型的优良性。运用模型判断附件3中15名目标客户购买电动车的可能性。
【1】建模
这里建立了四种模型:XGboost、LightGBM、Catboost和随机森林。
以 F1 值作为优化目标,使用贝叶斯优化的方法分别对 XGboost、LightGBM、Catboost
和随机森林这四个模型进行调参。
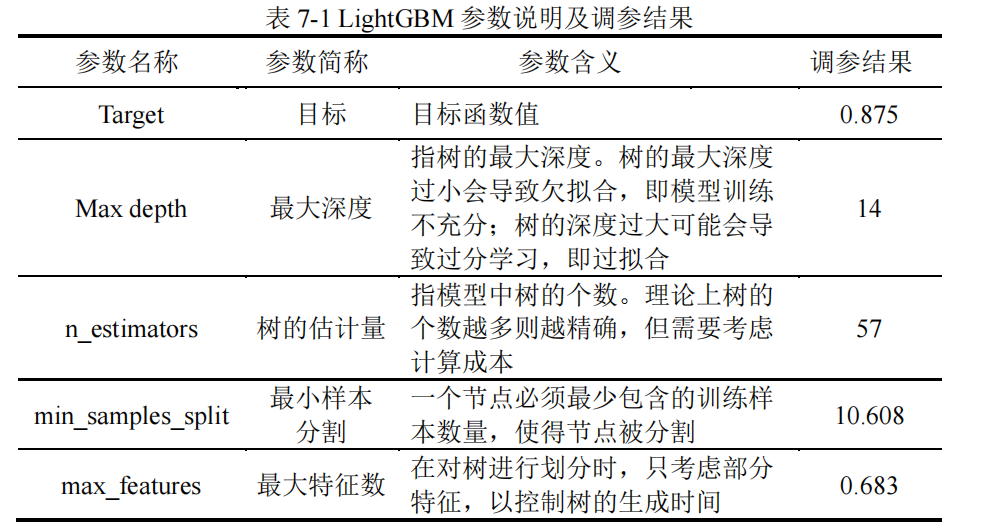
XGboost
##15. XGBoost \python3.0 import os os.environ['CUDA_VISIBLE_DEVICES'] = '1' #(3)xgb #需提前将自变量:X_jn 因变量 y 准备好 from sklearn.model_selection import RepeatedKFold def xgb_cv(gamma,max_depth,lambda0,subsample,colsample_bytree,min_child_weight ,eta,num_rounds,n_estimator,reg_alpha): params = { 'booster': 'gbtree', 'objective': 'multi:softmax', # 多分类的问题 #'objective': 'reg:logistic', # 多分类的问题 'num_class': 2, # 类别数,与 multisoftmax 并用 'gamma': min(gamma,0.39), # 用于控制是否后剪枝的参数,越大 越保守,一般 0.1、0.2 这样子。 'max_depth': int(max_depth), # 构建树的深度,越大越容易过拟合 'lambda': lambda0, # 控制模型复杂度的权重值的 L2 正则化项 参数,参数越大,模型越不容易过拟合。 'subsample': subsample, # 随机采样训练样本 'colsample_bytree':min(colsample_bytree,0.9), # 生成树时进行的列采样 'min_child_weight': int(min_child_weight), 'n_estimator':int(n_estimator), 'reg_alpha':reg_alpha, 'silent': 0, # 设置成 1 则没有运行信息输出,最好是设置为 0. 'eta': eta, # 如同学习率 'seed': 1000, 'nthread': 6, # cpu 线程数 } F1=[] kf = RepeatedKFold(n_splits=4, n_repeats=2, random_state=10) for train_index, test_index in kf.split(x): X_train, y_train = x.loc[train_index], y.loc[train_index] X_test, y_test = x.loc[test_index], y.loc[test_index] X_resampled, y_resampled = ADASYN().fit_sample(X_train, y_train) # 在训练 集采样 plst = params.items() dtrain = xgb.DMatrix(X_resampled, label=y_resampled) # 组成训练样本 model = xgb.train(plst, dtrain, int(num_rounds)) # xgboost 模型训练 test = xgb.DMatrix(X_test) test_pred=model.predict(test) F1.append(metrics.f1_score(y_test, test_pred)) return np.mean(F1) xgb_bo = BayesianOptimization( xgb_cv, {'gamma': (0.05, 0.39), 'max_depth': (3, 18), 'lambda0': (0.05,2), 'subsample': (0.4, 0.95), 'colsample_bytree': (0.3, 0.8), 'min_child_weight': (2, 8), 'eta': (0.005, 0.09), 'min_child_weight': (2, 8), 'num_rounds':(5,13), 'n_estimator':(50,300), 'reg_alpha':(0.001,0.95) } ) xgb_bo.maximize() xgb_bo.max xgb_bo.res xgb_bo.max #最优模型保存参数-存储贝叶斯过程数据 params = { 'booster': 'gbtree', 'objective': 'multi:softmax', # 多分类的问题 'num_class': 2, # 类别数,与 multisoftmax 并用 'gamma': 0.36, # 用于控制是否后剪枝的参数,越大越保守,一般 0.1、0.2 这样子。 'max_depth': 16, # 构建树的深度,越大越容易过拟合 'lambda': 0.21, # 控制模型复杂度的权重值的 L2 正则化项参数,参数越大,模型越不容易过拟合。 'subsample': 0.58, # 随机采样训练样本 'colsample_bytree': 0.33, # 生成树时进行的列采样 'min_child_weight': 2.4, 'silent': 0, # 设置成 1 则没有运行信息输出,最好是设置 为 0. 'eta': 0.06, # 如同学习率 'seed': 1000, 33 'nthread': 4, # cpu 线程数 } xgb_max=xgb_bo.max['params'] #将 xgb.max 转为模型可以使用的参数 def get_params(params,xgb_max): xgb_max=xgb_bo.max['params'] for k,v in zip(xgb_max.keys(),xgb_max.values()): if k!='num_rounds': #print(k,v) if k=='lambda0': params['lambda']=int(v) elif k in ['max_depth','min_child_weight','n_estimator']: params[k]=int(v) else: params[k]=v else: num_rounds = int(v) return params,num_rounds p0,n0=get_params(params,xgb_max) print(p0,n0) #将贝叶斯过程表存储 col=['target'] col.extend(list(xgb_max.keys())) C=[] for can in xgb_bo.res: target=can['target'] par=can['params'] c0=[target] c0.extend([int(par[k]) if k in ['max_depth','min_child_weight','lambda0','num_rounds'] else round(par[k],4) for k in list(par.keys())]) print(c0) C.append(c0) xg_bys=pd.DataFrame(C,columns=col) xg_bys.to_excel('F:/data/xgb 贝叶斯.xls') from xgboost import XGBClassifier clf2 = XGBClassifier(booster= 'gbtree', objective='multi:softmax',num_class=2, gamma=0.11696860130369573, max_depth=8, reg_lambda=0, subsample= 0.8655511495012012, colsample_bytree= 0.40700451581623387, min_child_weight= 2, silent= 0, eta=0.05427410755931234, seed=1000, nthread= 4, n_estimator= 255, reg_alpha=0.19559357671270297,num_rounds=12) clf2.fit(X_resampled,y_resampled) y_pred=clf2.predict(X_test) from sklearn.metrics import accuracy_score print('auc_score:{}'.format(accuracy_score(y_test, y_pred))) print('Precision',metrics.precision_score(y_test, y_pred)) print('Recall',metrics.recall_score(y_test, y_pred)) print('F1-score:',metrics.f1_score(y_test, y_pred))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
LightGBM
##16. LightGBM \python3.0 from bayes_opt import BayesianOptimization from lightgbm import LGBMClassifier import lightgbm as lgb from sklearn import datasets from sklearn.model_selection import train_test_split import numpy as np from sklearn.metrics import roc_auc_score, accuracy_score def lgb_cv(n_estimators, min_samples_split, max_features, max_depth): lgb=LGBMClassifier(n_estimators=int(n_estimators), min_samples_split=int(min_samples_split), max_features=min(max_features, 0.999), # float max_depth=int(max_depth), random_state=2 ) lgb.fit(X_resampled,y_resampled) y_pred=lgb.predict(X_test) return metrics.f1_score(y_test, y_pred) lgb_bo = BayesianOptimization( lgb_cv, {'n_estimators': (30, 250), 'min_samples_split': (2, 25), 'max_features': (0.1, 0.999), 'max_depth': (5, 15)} ) lgb_bo.maximize() lgb_bo.max gbm = LGBMClassifier(n_estimators=57, max_depth=14, min_samples_split=10.60807228663149, max_features=0.6829707285490627 gbm.fit(X_resampled,y_resampled) from sklearn.metrics import accuracy_score from sklearn import metrics print('auc_score:{}'.format(accuracy_score(y_test, y_pred))) print('Precision',metrics.precision_score(y_test, y_pred)) 36 print('Recall',metrics.recall_score(y_test, y_pred)) print('F1-score:',metrics.f1_score(y_test, y_pred)) ### lgb 效果最好,用来预测 data=pd.read_csv("F:/data/brand1.csv",encoding='gbk') data.head() X=data.drop(['num'], axis=1) #删除列 y_pred=gbm.predict(X) y_pred #预测每个类别的概率,这是叶子中相同类别的训练样本的分数 result=gbm.predict_proba(X) result = pd.DataFrame(result) result.head() result.to_csv("F:/data/ypred.csv",index=False)#转换成 csv 文件 data=pd.read_csv("F:/data/ypred.csv",encoding='gbk') data.head() #查看概率分布 sns.distplot(data['1']) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
CatBoost
##17. CatBoost \python3.0 import pandas as pd, numpy as np from sklearn.model_selection import train_test_split, GridSearchCV from sklearn import metrics import catboost as cb import catboost as CatBoost import pandas as pd import numpy as np from catboost import CatBoostClassifier, CatBoost, Pool, cv from bayes_opt import BayesianOptimization def cab_cv(depth, learning_rate, l2_leaf_reg, iterations): cab=cb.CatBoostClassifier() cab.fit(X_resampled,y_resampled) y_pred=cab.predict(X_test) return metrics.f1_score(y_test, y_pred) cab_bo = BayesianOptimization( cab_cv, {'depth': (5,15), 'learning_rate': (0.03,0.15), 'l2_leaf_reg': (1,9), 'iterations': (300, 500)} ) cab_bo.maximize() cab_bo.max #用最优参数拟合数据 clf = cb.CatBoostClassifier(depth=7, iterations=320, l2_leaf_reg=5.521070327796334, learning_rate=0.06522340040216315,loss_function="Logloss") clf.fit(X_resampled,y_resampled) y_pred=clf.predict(X_test) from sklearn.metrics import accuracy_score from sklearn import metrics print('auc_score:{}'.format(accuracy_score(y_test, y_pred))) print('Precision',metrics.precision_score(y_test, y_pred)) print('Recall',metrics.recall_score(y_test, y_pred)) print('F1-score:',metrics.f1_score(y_test, y_pred))- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
【2】模型评估
在实际的汽车购买场景中,我们更关心客户是否会购买汽车,即是取值为“1”的
样本被准确预测的比例,因此使用 AUC 值和 F1 值对模型的预测效果进行评估。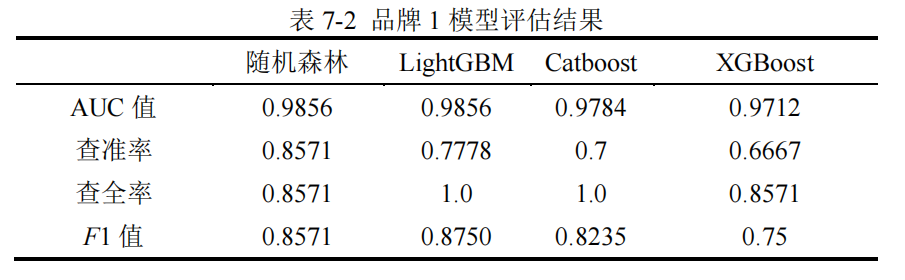
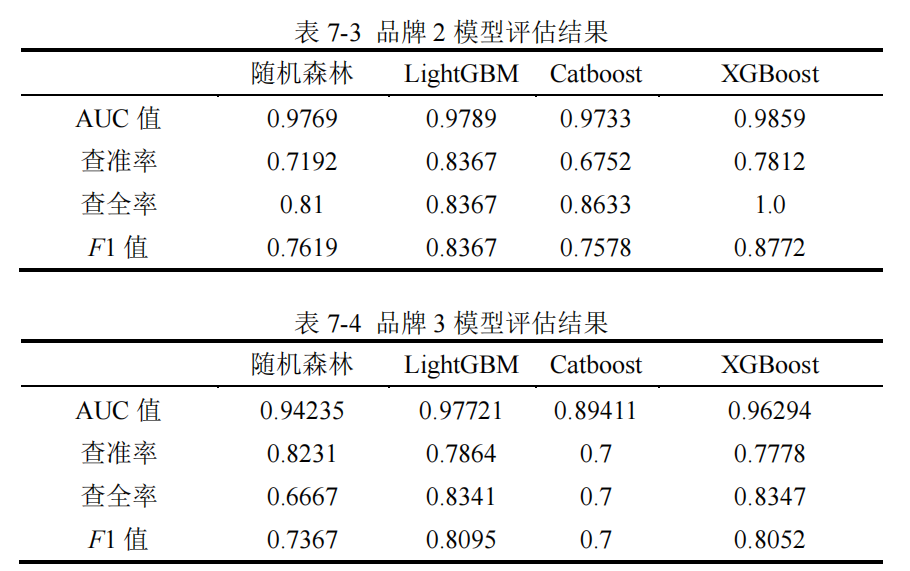
【3】模型预测
在建立完模型的基础上,分别选取三种品牌中表现最优的模型,对附录 3 中的客户
数据进行预测。
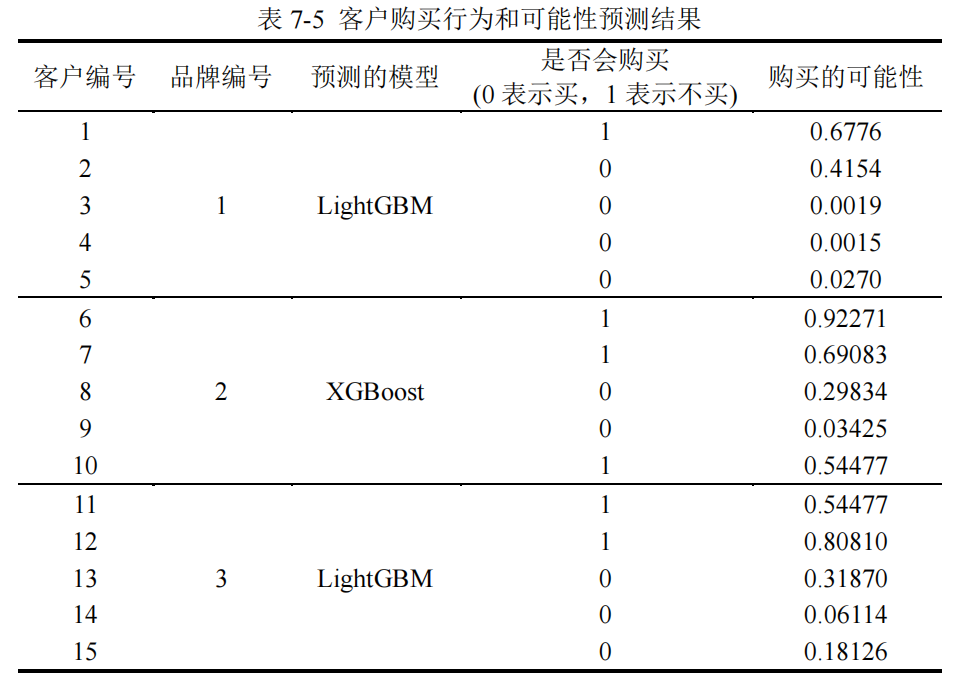
-
相关阅读:
Docker 安装redis
Unity模拟薄膜干涉效果
LeetCode59-螺旋矩阵II
网络分析笔记06:解析TCP/IP的IP协议
CPC训练联盟程序设计夏令营(四)
小恐龙快跑,不要被逮到拉~ python制作小恐龙游戏
【读书笔记】《我在北京送快递》——记录的意义
基于SpringBoot+Vue的点餐管理系统
c/c++如何实现根据磁盘空间管理自己的日志文件案例
以SQLserver为例的Dapper详细讲解
- 原文地址:https://blog.csdn.net/wxfighting/article/details/126123252