提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

又是没有见过的新题型捏~（知识点：排列组合问题首选搜索算法）

一、题目

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例

示例 1：
输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例 2：
输入：digits = “”
输出：[]

示例 3：
输入：digits = “2”
输出：[“a”,“b”,“c”]

提示

0 <= digits.length <= 4
digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

二、思路

1.数学

一开始想遍历整个结果数组，用数学方法确定每次要填的字母，每次填一个，就需要大概 n*3（4）^n次s.append()运算。整体思路没毛病就是对数学要求比较高，公式很容易写错，整的像个数学题不像个编程题了。

下面介绍一哈回溯和队列的思路

2.dfs+回溯

关键字“所有组合”，如果不止局限于一维数组，而把组合过程看成一棵树，很容易想到dfs（递归实现）遍历每种情况（搜索算法）
搜索算法首先需要找到子问题，并在当前递归层对该子问题进行操作。本题子问题就是每一个数字所标志字符的加入。就像：

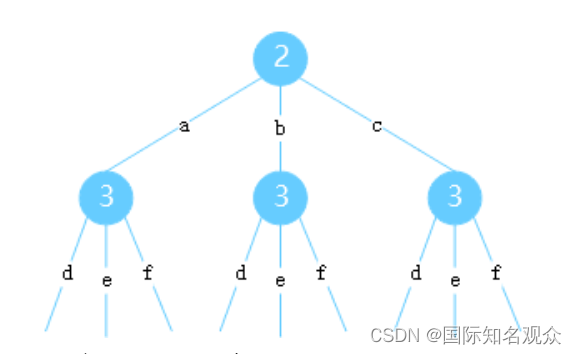
3.BFS＋队列

使用队列，先将输入的 digits 中第一个数字对应的每一个字母入队，然后将出队的元素与第二个数字对应的每一个字母组合后入队…直到遍历到 digits 的结尾。最后队列中的元素就是所求结果。

三、代码

1.数学 （python）

class Solution:
    def letterCombinations(self, digits: str) -> list[str]:
        #映射
        reflect=['abc','def','ghi','jkl','mno','pqrs','tuv','wxyz']
        #字符串长度
        n=len(digits)
        #返回的数组每位的字符宽度（即重复多少次）,生成的是倒着的
        re_wid=[1]
        for i in range(1,n+1):
            temp=int(digits[n-i])
            if(temp==7 or temp==9):
                re_wid.append(re_wid[i-1]*4)
            else:
                re_wid.append(re_wid[i-1]*3)
        #返回数组长度
        re_len=re_wid[-1]
        #返回数组
        re_list=["" for i in range(re_len)]
        #digits中每个数字（即返回数组中的字符宽度）一轮
        for i in range(n):
            index=int(digits[i])
            #遍历re_list，将本轮字符添加上
            for j in range(re_len):
                #%和//求位置               
                re_list[j]+=reflect[index-2][j%re_wid[n-i]//re_wid[n-1-i]]
        #规范输出
        if(re_list[0] == ''):
            return []
        else:
            return re_list

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

2.dfs（＋回溯）（python）

class Solution:
    def letterCombinations(self, digits: str) -> list[str]:
        #特殊情况
        if(digits==""):
            return []
        #映射
        reflect=['abc','def','ghi','jkl','mno','pqrs','tuv','wxyz']
        #返回数组
        re_list=[]
        #字符串长度
        n=len(digits)

        #本轮传入的字符串和即将加入的是哪个数字(index是digits中下标)
        def dfs(index,s):
            #终止条件，可以加入结果数组了
            if(len(s)==n):
                re_list.append(s)
                #终止
                return
            #对于此层每个数字
            for j in range(len(reflect[int(digits[index])-2])):
                dfs(index+1,s+reflect[int(digits[index])-2][j])
        dfs(0,'')
        return re_list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24