注意力提示

因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。 在注意力机制的背景下，我们将自主性提示称为查询（query）。 给定任何查询，注意力机制通过注意力汇聚（attention pooling） 将选择引导至感官输入（sensory inputs，例如中间特征表示）。 在注意力机制中，这些感官输入被称为值（value）。 更通俗的解释，每个值都与一个键（key）配对， 这可以想象为感官输入的非自主提示。

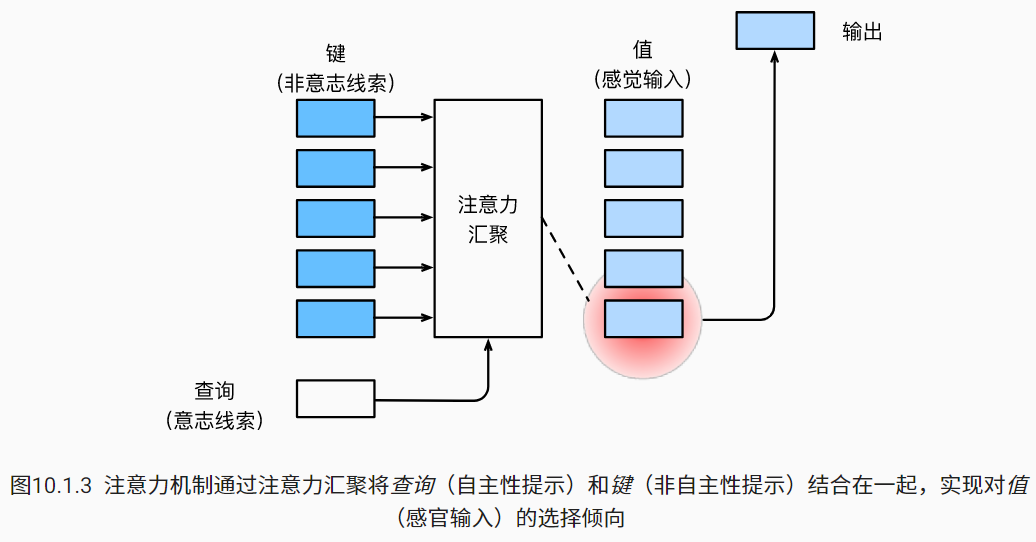
模型如上，进行了汇聚。

注意力汇聚：Nadaraya-Watson 核回归

1.平均汇聚

这个还是比较草率的，甚至忽略了输入x_i

效果图如图，圆点为训练数据（包含噪声了）：

2.非参数注意力汇聚(N-W核回归）

N-W核回归根据输入的位置对输出y_i进行了加权：

其中K是核，受此启发核注意力机制框架的角度（图10.1.3，上面有）进行重写成一个更通用的注意力汇聚公式：

代码实现
有点疑问：f(x)最外围的累加在哪体现了？

# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入（例如：同样的查询）
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train)) # 重复张量的元素，最外围的累加的实现吧。
# x_train包含着键。attention_weights的形状：(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值（y_train）之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意力权重
y_hat = torch.matmul(attention_weights, y_train)

1
2
3
4
5
6
7
8
9

该方法具有一致性（consistency）的优点： 如果有足够的数据，此模型会收敛到最优结果。

3.带参数注意力汇聚

与无参数的方法相比略有不同， 在下面的查询 x 和键 xi 之间的距离乘以可学习参数 w：

假定两个张量的形状分别是 (n,a,b) 和 (n,b,c) ， 它们的批量矩阵乘法输出的形状为 (n,a,c) 。通过使用torch.bmm()计算矩阵相乘，第一维默认为batch_size，要求两个张量相等。
定义一个使用小批量矩阵乘法的带参数N-W版本：

class NWKernelRegression(nn.Module):
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.w = nn.Parameter(torch.rand((1,), requires_grad=True))

    def forward(self, queries, keys, values):
        # queries和attention_weights的形状为(查询个数，“键－值”对个数)
        queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))
        self.attention_weights = nn.functional.softmax(
            -((queries - keys) * self.w)**2 / 2, dim=1)
        # values的形状为(查询个数，“键－值”对个数)
        #在return的代码种，首先把attention_weights变为(查询个数，1，键值对个数），把values变为(查询个数，”键值对个数“，1），此时算出来的结果为（查询个数，1，1）然后.reshape(-1)则不分行列变为1串
        return torch.bmm(self.attention_weights.unsqueeze(1),
                         values.unsqueeze(-1)).reshape(-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

注意力评分函数

把10.2.6中的高斯核指数部分视为注意力评分函数，简称评分函数，下图说明了如何将注意力汇聚的输出计算成为值的加权和， 其中 a 表示注意力评分函数。

其数学表达为：

选择不同的注意力评分函数a将导致不同的注意力汇聚操作。

1.掩蔽softmax操作

某些文本序列被填充了没有意义的特殊词元。 为了仅将有意义的词元作为值来获取注意力汇聚， 我们可以指定一个有效序列长度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置，下面代码把其中任何超出有效长度的位置都被掩蔽并置为0。

#@save
def masked_softmax(X, valid_lens):
    """通过在最后一个轴上掩蔽元素来执行softmax操作"""
    # X:3D张量，valid_lens:1D或2D张量
    if valid_lens is None:
        return nn.functional.softmax(X, dim=-1)
    else:
        shape = X.shape
        if valid_lens.dim() == 1:
            valid_lens = torch.repeat_interleave(valid_lens, shape[1])
        else:
            valid_lens = valid_lens.reshape(-1)
        # 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0
        X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
                              value=-1e6)
        return nn.functional.softmax(X.reshape(shape), dim=-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

2.加性注意力

数学公式：

查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小）
代码实现

#@save
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # queries's size : torch.Size([2, 1,1, 8])
		# keys's size : torch.Size([2, 1,10, 8])
		# features's size : torch.Size([2, 1, 10, 8])
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1) # 比如原来是[[1],[2],[3]],变为了[1,2,3]
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        return torch.bmm(self.dropout(self.attention_weights), values)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

3.缩放点积注意力

数学表达

代码实现

#@save
class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

这一直说的“键-值”对的个数，我不是很理解到底是什么玩意。

Bahdanau 注意力

可微注意力模型是一种一个没有严格单向对齐限制的模型，在预测词元时，如果不是所有输入词元都相关，模型将仅对齐（或参与）输入序列中与当前预测相关的部分。这是通过将上下文变量视为注意力集中的输出来实现的。
网络架构如下图所示（是对9.7的一个改进）：

数学描述：

代码实现
根据网络架构可以看出：

1. 编码器在所有时间步的最终层隐状态，将作为注意力的键和值；
2. 上一时间步的编码器全层隐状态，将作为初始化解码器的隐状态；
3. 编码器有效长度（排除在注意力池中填充词元）。
   为解码器的输入。

class Seq2SeqAttentionDecoder(AttentionDecoder):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
        self.attention = d2l.AdditiveAttention(
            num_hiddens, num_hiddens, num_hiddens, dropout)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(
            embed_size + num_hiddens, num_hiddens, num_layers,
            dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        # outputs的形状为(batch_size，num_steps，num_hiddens).
        # hidden_state的形状为(num_layers，batch_size，num_hiddens)
        outputs, hidden_state = enc_outputs
        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

    def forward(self, X, state):
        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).
        # hidden_state的形状为(num_layers,batch_size,
        # num_hiddens)
        enc_outputs, hidden_state, enc_valid_lens = state
        # 输出X的形状为(num_steps,batch_size,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        outputs, self._attention_weights = [], []
        for x in X:
            # query的形状为(batch_size,1,num_hiddens)
            query = torch.unsqueeze(hidden_state[-1], dim=1)
            # context的形状为(batch_size,1,num_hiddens)
            context = self.attention(
                query, enc_outputs, enc_outputs, enc_valid_lens)
            # 在特征维度上连结
            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
            # 将x变形为(1,batch_size,embed_size+num_hiddens)
            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
            outputs.append(out)
            self._attention_weights.append(self.attention.attention_weights)
        # 全连接层变换后，outputs的形状为
        # (num_steps,batch_size,vocab_size)
        outputs = self.dense(torch.cat(outputs, dim=0))
        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
                                          enc_valid_lens]

    @property
    def attention_weights(self):
        return self._attention_weights
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

多头注意力

希望模型可以基于相同的注意力机制学习到不同的行为， 然后将不同的行为作为知识组合起来， 捕获序列内各种范围的依赖关系。

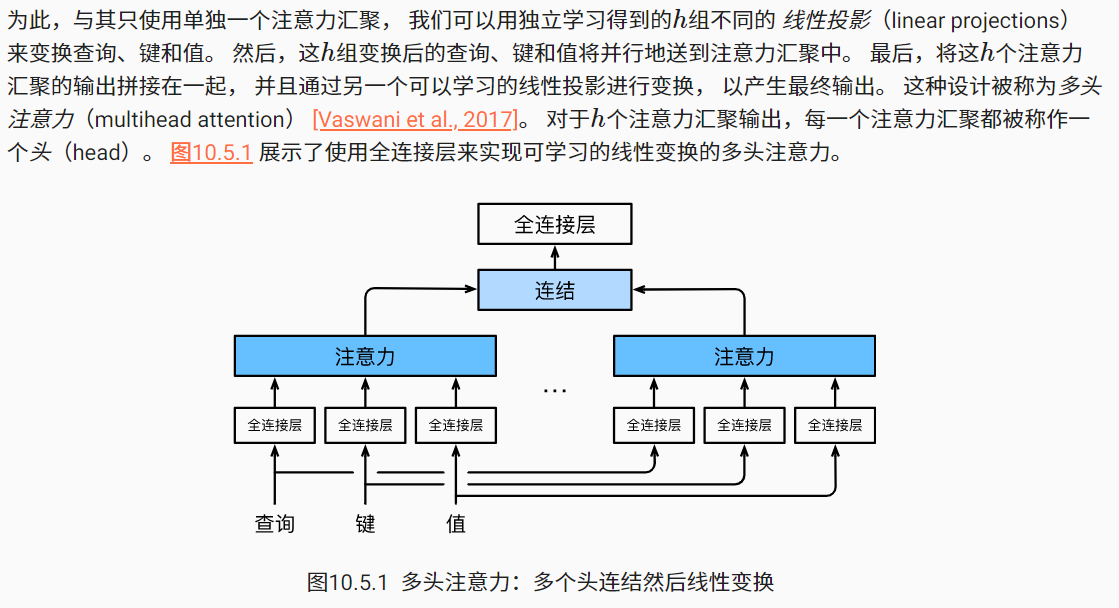
模型的数学表示：

代码实现

在实现过程中，我们选择缩放点积注意力作为每一个注意力头。 为了避免计算代价和参数代价的大幅增长， 我们设定 p_q=p_k=p_v=p_o/h 。 值得注意的是，如果我们将查询、键和值的线性变换的输出数量设置为 p_qh=p_kh=p_vh=p_o ， 则可以并行计算 h 个头。 在下面的实现中， po 是通过参数num_hiddens指定的。

#@save
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
        # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
        # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

这个类使用了下面的两个定义的转置参数：

#@save
def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    # 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
    # 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，
    # num_hiddens/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)

    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])


#@save
def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

自注意力和位置编码

有了注意力机制之后，我们将词元序列输入注意力池化中， 以便同一组词元同时充当查询、键和值。 具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。 由于查询、键和值来自同一组输入，因此被称为 自注意力（self-attention）， 也被称为内部注意力（intra-attention）。

代码实现

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                                   num_hiddens, num_heads, 0.5)
attention.eval()
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape # torch.Size([2, 4, 100])
1
2
3
4
5
6
7

位置编码

因为循环神经网络是逐个的重复地处理词元的， 而自注意力则因为并行计算而放弃了顺序操作。 为了使用序列的顺序信息，我们通过在输入表示中添加 位置编码（positional encoding）来注入绝对的或相对的位置信息。 位置编码可以通过学习得到也可以直接固定得到。

基于正弦函数和余弦函数的固定位置编码

代码实现
比较简单

#@save
class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

绝对位置信息

在二进制表示中，较高比特位的交替频率低于较低比特位， 只是位置编码通过使用三角函数在编码维度上降低频率。 由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间

相对位置信息

上面的位置编码还可以模型学习得到输入序列中相对位置信息，对于任何确定的位置偏移 δ ，位置 i+δ 处 的位置编码可以线性投影位置 i 处的位置编码来表示。

Transformer

ransformer模型完全基于注意力机制，没有任何卷积层或循环神经网络层。

TIPS

torch.repeat_interleave

torch.repeat_interleave(input, repeats, dim=None) → Tensor

1
2

重复张量的元素
输入参数：

input (类型：torch.Tensor)：输入张量
repeats（类型：int或torch.Tensor）：每个元素的重复次数。repeats参数会被广播来适应输入张量的维度
dim（类型：int）需要重复的维度。默认情况下，将把输入张量展平（flatten）为向量，然后将每个元素重复repeats次，并返回重复后的张量。

疑问

10.6.2三种网络比较的数学计算推导