• 上采样方式（反卷积、插值、反池化）

    目录

    1.反卷积

    （1）正常卷积

    （2）反卷积

    2.反池化

    3.插值法 

    （1）最近邻插值

     （2）线性插值

    1.反卷积

    反卷积：反卷积可以理解为卷积操作的逆运算，反卷积并不能复原成原图像，因为卷积操作会造成值的损失，它仅仅是将卷积过程中的步骤反向变换一次，因此它还可以被称为转置卷积。

    反卷积公式：H_{out}=(H_{in}-1)\times stride+K-2P

    如果有空洞：H_{out}=(H_{in}-1)\times stride-2\times P +dilation\times(K-1)+1

    那么，反卷积是怎么操作的呢？

    首先我们看一看正常卷积是怎么计算的。

    （1）正常卷积

    假设输入为4*4，kernel_size为3*3，padding为0，stride为1

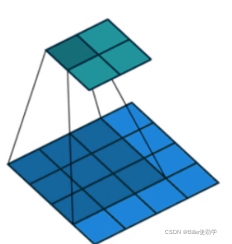
    我们都知道卷积的操作就是卷积核在特征图上进行滑动计算（如下图），这个过程是相乘再求和的，那在底层代码中4*4的特征图是怎么和3*3的卷积核进行相乘操作的呢？

     

    先看结论：

    图像：I_{16*1}        卷积核：K_{4*16}        输出：O_{4*1} = K_{4*16} * I_{16*1}

    再看过程：

    • 针对单张特征图，输入4*4的尺寸会被展平（flatten）成16*1的序列，16为输入特征图的像素个数，1为图片的个数，即单张图片。
    • 将3*3的卷积核进行补0操作，变成与输入大小相同的4*4的矩阵，再展平为1*16，已知输出为2*2大小，故卷积核为4*16的矩阵。其中4为输出特征图的像素数量，16为输入特征图的像素数量。
    • 将4*16的卷积核与16*1的特征图进行矩阵相乘操作，就得到了输出的4*1的序列，再进行reshape操作， 得到最终的2*2的特征图。

    （2）反卷积

    假设图像尺寸为2*2，卷积核为3*3， padding = 0， stride = 1

    反卷积（转置卷积）在底层是怎么计算的呢？其实也是相同的原理

     

    先看结论：

    图像：I_{4*1}        卷积核：K_{16*4}        输出：O_{16*1} = K_{16*4} * I_{4*1}

    再看过程：

    • 将输入2*2图片拉成一个一维向量4*1
    • 卷积核由3*3变为2*2，进行剔除操作，16为输出图像的像素值数量，4为输入的特征图像素数量
    • 将卷积核乘图像得到一个16个像素值的一维向量16*1，再进行reshape操作，转为4*4的特征图

    由上得出，两个操作的卷积核在形状上是转置的关系（权值不相同），故对图像进行卷积操作，再进行转置卷积，两个图像是不相等的。故该操作是不可逆的。

    2.反池化

    反池化顾名思义就是池化的逆操作。

    对于最大池化的反池化操作：在进行最大池化时，网络会记录最大值的索引位置，如下图max-pooling操作中黄色窗口中（左图）的0.8为最大值，网络会记住该值得索引位置，如右边的4×4网格中的标记所示，这样在进行反池化时，就可以将值放到对应的最大值索引的位置，其余位置补0，如下图uppooling操作黄色窗口（右图）中将1.3放到了之前记录的最大索引的位置，其余位置补0。

    如最大池化代码中的return_indices就表示是否保存最大值的索引，以备反池化的时候使用： 

     反最大池化代码，indices为保存的最大值索引位置

     

    对于平均池化的反池化操作：无需像最大池化那样记录最大值得索引，在反池化时，只需将每个值填入相应的窗口即可。如下图所示：

    3.插值法 

    然后就是插值法，插值的方式有很多种,本文介绍最近邻插值和双线性插值。

    • 计算效果：最近邻插值算法 < 双线性插值 
    • 计算速度：最近邻插值算法 > 双线性插值

    （1）最近邻插值

            最简单的一种插值方法，不需要计算，在待求像素的四邻像素中，将距离待求像素最近的邻像素灰度赋给待求像素。（缺点：输出的图像会有锯齿状）

            设i+u，j+v（i，j为正整数，u，v为大于零小于1的小数，下同）为待求像素坐标，则待求像素灰度的值f（i+u，j+v）

    公式如下：src为原来的坐标，dst为待求的坐标

    如图：图像由原来的3×3变为4×4大小的图像

    srcWidth为3；dstWidth为4

    以待求图的第一个点（0,0）为例：

    srcX = （0*（3/4），0*（3/4））=（0,0）= 234

    得出的（0,0）就为原图坐标，则待求点的值就用求出的相对应原图位置的值来代替

    以待求图的（3,0）点为例：

    srcX = （（3*（3/4），（0*（3/4））=（3*0.75,0）=（2.25）=（2,0）=89

    采用四舍五入的方法求最近坐标 

     （2）线性插值

    ①单线性插值

     

    我们根据一个例子来看一下具体是怎么计算的。

    将2*2的图片扩大为4*4的图片：

    计算①到⑫的值

    公式：y=y_0+\frac{y_1-y_0}{x_1-x_0}(x-x_0)，或者上面两个公式都可，计算y的值

    注：xi为坐标，yi为xi相对应的值

    ①：x = 2,  x0 = 1, x1 = 4, y0 = 4, y1 = 6

    y=4+\frac{6-4}{4-1}(2-1)=4.66

    ②：x = 3, x0 = 1, x1 = 4, y0 = 4, y1 = 6

    y=4+\frac{6-4}{4-1}(3-1)=5.33

    ③：x = 2, x0 = 1, x1 = 4, y0 = 4, y1 = 10

    y=4+\frac{10-4}{4-1}(2-1)=6

    ④：x = 3, x0 = 1, x1 = 4, y0 = 4, y1 = 10

    y=4+\frac{10-4}{4-1}(3-1)=8

    ⑤：x = 2, x0 = 1, x1 = 4, y0 = 6, y1 = 8

    y=6+\frac{8-6}{4-1}(2-1)=6.66

    ②双线性插值

            双线性插值又叫一阶插值法，它要经过三次插值才能获得最终结果，是对最近邻插值法的一种改进，先对两水平方向进行一阶线性插值，然后再在垂直方向进行一阶线性插值。 

     

    参考

    上采样方法综述：线性插值，转置卷积，上池化

  • 相关阅读:
    读写 XML/JSON/INI 和 UBJSON 等格式的数据文件的统一接口
    JVM | 垃圾回收器（GC）- Java内存管理的守护者
    stm32cubemx hal学习记录：TIMER输入捕获
    Go语言基准测试(benchmark)三部曲之三：提高篇
    8.5 数据结构——归并排序和基数排序
    SQLMAP自动注入-request参数
    使用pytest和allure框架实现自动化测试报告优化
    互联网刚需岗位 前景一片大好？
    面试经典150题——Day33
    .NET 反射 Reflect
  • 原文地址：https://blog.csdn.net/m0_45447650/article/details/125624971