提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

如果只给定一个二叉树前序遍历数组pre和中序遍历数组in，
能否不重建树，而直接生成这个二叉树的后序数组并返回
已知二叉树中没有重复值

解题思路

定义f函数void类型
把先序遍历数组,跟范围L1, R1.
把中序遍历数组,跟范围L2, R2
填后序遍历数组,范围L3, R3,三段范围等长
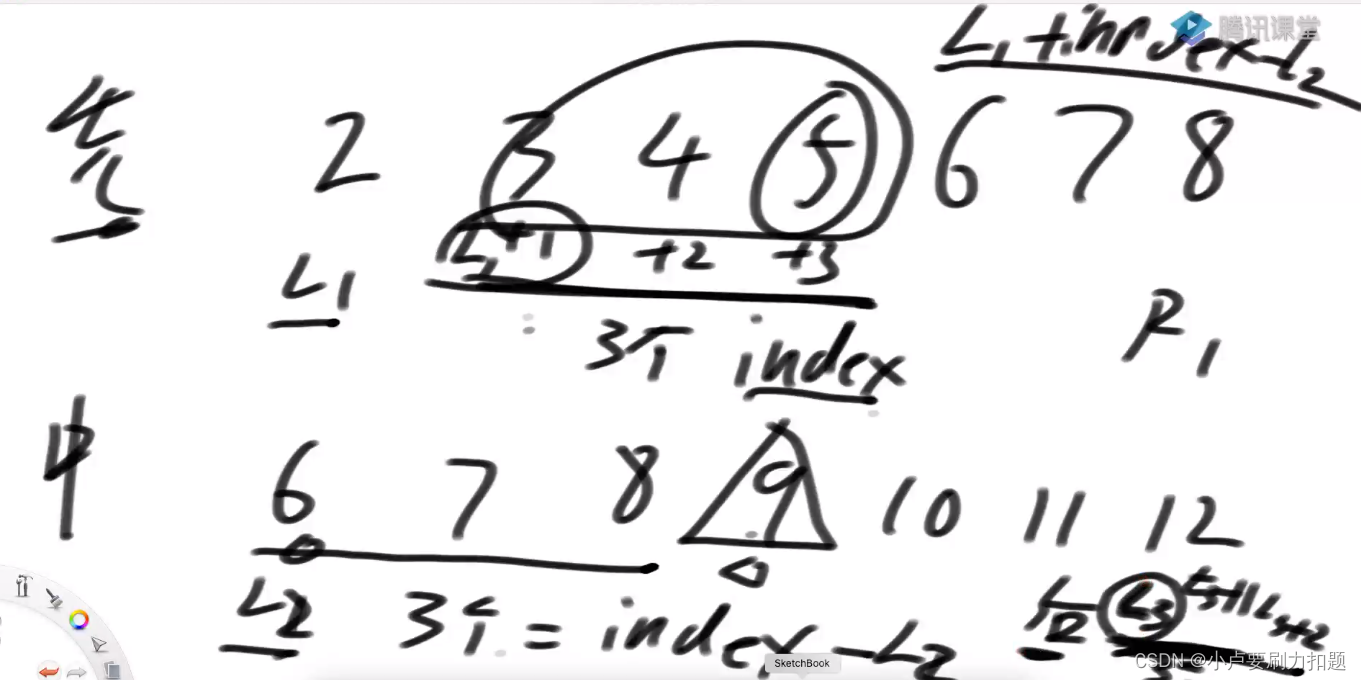在中序遍历定位X确定左树跟右树规模
但定位了前序,中序,后序的X后
调用递归,生成左树,右树

代码

	public static int[] preInToPos1(int[] pre, int[] in) {
		if (pre == null || in == null || pre.length != in.length) {
			return null;
		}
		int N = pre.length;
		int[] pos = new int[N];
		process1(pre, 0, N - 1, in, 0, N - 1, pos, 0, N - 1);
		return pos;
	}

	// L1...R1 L2...R2 L3...R3
	public static void process1(int[] pre, int L1, int R1, int[] in, int L2, int R2, int[] pos, int L3, int R3) {
		if (L1 > R1) {
			return;
		}
		if (L1 == R1) {
			pos[L3] = pre[L1];
			return;
		}
		pos[R3] = pre[L1];
		int mid = L2;
		for (; mid <= R2; mid++) {
			if (in[mid] == pre[L1]) {
				break;
			}
		}
		int leftSize = mid - L2;
		process1(pre, L1 + 1, L1 + leftSize, in, L2, mid - 1, pos, L3, L3 + leftSize - 1);
		process1(pre, L1 + leftSize + 1, R1, in, mid + 1, R2, pos, L3 + leftSize, R3 - 1);
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

使用哈希表来代替遍历查找过程

	public static int[] zuo(int[] pre, int[] in) {
		if (pre == null || in == null || pre.length != in.length) {
			return null;
		}
		int N = pre.length;
		HashMap<Integer, Integer> inMap = new HashMap<>();
		for (int i = 0; i < N; i++) {
			inMap.put(in[i], i);
		}
		int[] pos = new int[N];
		func(pre, 0, N - 1, in, 0, N - 1, pos, 0, N - 1, inMap);
		return pos;
	}

	public static void func(int[] pre, int L1, int R1, int[] in, int L2, int R2, int[] pos, int L3, int R3,
			HashMap<Integer, Integer> inMap) {
		if (L1 > R1) {
			return;
		}
		if (L1 == R1) {
			pos[L3] = pre[L1];
		} else {
			pos[R3] = pre[L1];
			int index = inMap.get(pre[L1]);
			func(pre, L1 + 1, L1 + index - L2, in, L2, index - 1, pos, L3, L3 + index - L2 - 1, inMap);
			func(pre, L1 + index - L2 + 1, R1, in, index + 1, R2, pos, L3 + index - L2, R3 - 1, inMap);
		}
	}```

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29