贝塞尔曲线参考 : https://github.com/venshine/BezierMaker

一、德卡斯特里奥算法

---

贝塞尔曲线的 三阶 / 四阶 / 五阶 曲线的绘制 , 都是依赖于其低阶贝塞尔曲线实现的 ,

三阶贝塞尔曲线 是由 二阶贝塞尔曲线 实现的 ,

四阶贝塞尔曲线 是由 三阶贝塞尔曲线 实现的 ;

德卡斯特里奥算法 可以实现 贝塞尔曲线 降阶的效果 ;

下面开始介绍 德卡斯特里奥算法 ;

在 向量 $AB$ 上 选择 $C$ 点 ,

$C$ 点将 $AB$ 向量切割成比例为 $u:1-u$ ,

也就是 $A$ 到 $C$ 的距离 $|AC|$ , 与 $A$ 到 $B$ 的距离 $|AB|$ , 其比值为 $u$ , 写成公式就是如下形式 :

$$|AC|:|AB|=u$$

$A$ 到 $B$ 的距离 $|AB|$ 全长为 $1$ ,

$A$ 到 $C$ 的距离 $|AC|$ 比例占到全长的 $u$ , $u$ 的取值范围是 $0$ ~ $1$ 之间的浮点值 ,

$C$ 到 $B$ 的距离 $|CB|$ 比例占到全长的 $1-u$ ;

再回到贝塞尔曲线中 ,

上图是 $P_0$ 到 $P_2$ 的 二阶 贝塞尔曲线 , $P_0$ 是起始点 , $P_2$ 是终止点 , $P_1$ 是控制点 ;

首先 通过 一阶等式 , 在 $P_0$ 到 $P_1$ 之间确定出 $P_0^1$ 点 , $P_0$ 到 $P_0^1$ 点占 整个 $P_0$ 到 $P_1$ 的比例为 $u$ ;

然后 通过 一阶等式 , 在 $P_1$ 到 $P_2$ 之间确定出 $P_1^1$ 点 , $P_1$ 到 $P_1^1$ 点占 整个 $P_1$ 到 $P_2$ 的比例为 $u$ ;

最后 通过 一阶等式 , 在 $P_0^1$ 到 $P_1^1$ 之间确定出 $P_0^2$ 点 , $P_0^1$ 到 $P_0^2$ 点占 整个 $P_0^1$ 到 $P_1^1$ 的比例为 $u$ ;

最终得到如下等式 :

$$\frac{P_0{P}_0^1}{P_0^1{P}_1}=\frac{P_1{P}_1^1}{P_1^1{P}_2}=\frac{P_0^1{P}_0^2}{P_0^2{P}_1^1}=u$$

当 $u$ 从 $0$ ~ $1$ 进行变化时 , $P_0^2$ 点形成的曲线就是 二阶贝塞尔曲线 ;

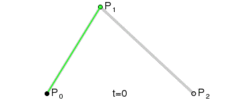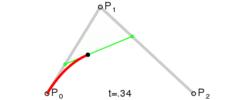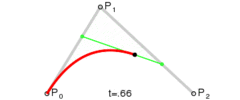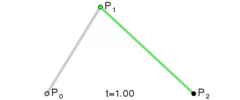
( 网上找的图片 , 图片中的 $t$ 也就是上面说的比例 $u$ )

二阶贝塞尔曲线中的 $P_0^2$ 点 ,

由 起始点 $P_0$ 到 控制点 $P_1$ 组成的向量 , 和 由 控制点 $P_1$ 到 终止点 $P_2$ 组成的向量 ,

这两个向量 根据比例 $u$ 决定的 一阶贝塞尔曲线 $P_0^1$ 到 $P_1^1$ 向量 根据比例 $u$ 确定的 ,

也就是 $P_0^2$ 点 由 一阶贝塞尔曲线 $P_0^1$ 到 $P_1^1$ 向量 确定 ;

上述操作 , 将 二阶贝塞尔曲线 , 降阶成了 一阶贝塞尔曲线 ;

二、贝塞尔曲线递推公式

---

由上面的结论进行类推 :

二阶贝塞尔曲线 ( 起止点 + $1$ 个控制点 ) 由 $2$ 条 一阶贝塞尔曲线 确定 ,

三阶贝塞尔曲线 ( 起止点 + $2$ 个控制点 ) 由 $2$ 条 二阶贝塞尔曲线 确定 ,

四阶贝塞尔曲线 ( 起止点 + $3$ 个控制点 ) 由 $2$ 条 三阶贝塞尔曲线 确定 ,

$⋮$

$n$阶贝塞尔曲线 ( 起止点 + $n-1$ 个控制点 ) 由 $2$ 条 $n-1$ 阶贝塞尔曲线 确定 ;

贝塞尔曲线递推公式如下 :

P i k = { P i , k = 0 ( 1 − t ) P i k − 1 + t P i + 1 k − 1 , k = 1 , 2 , ⋯   , n ; i = 0 , 1 , ⋯   , n − k P_i^k = {Pi,k=0(1−t)Pk−1i+tPk−1i+1,k=1,2,⋯,n;i=0,1,⋯,n−k

Pik​={Pi​,k=0(1−t)Pik−1​+tPi+1k−1​,k=1,2,⋯,n;i=0,1,⋯,n−k​