幂级数求和难吗？细节很重要

引言

无穷级数这部分考研主要是三部分内容

1. 级数敛散性判定
2. 幂级数求和
3. 傅里叶级数

这块内容我在大一学期的时候没有好好学，复习这块内容的也是非常的吃力。个人认为难点主要是：
①内容本身就很难，对于无穷项的处理很抽象
②不直观，无法像重积分借助直观的图形来表达
③难题灵活，难以找到套路和规律
当然，为了解决以上的难点，我们只能慢慢来。这篇博客我想主要说一下在幂级数求和中的一些问题。老规矩，以一道题目作为例子：
$$求\sum _{n=1}^{\infty }\frac{x^{n-1}}{n{2}^n}的和函数$$

错误分析

错误一：未求收敛域

有的人一上来急忙开始求和函数，又是凑项又是求导求积分的，结果没求收敛域白白丢分。所以要牢记：求和函数前先求收敛域，以便于后续我们讨论分段函数的取值范围。

错误二：求导，求积写法混乱

上述两种写法那个正确呢？Clearly the latter~
很明显我们是要得到求导后的结果，所以应该是在求导后结果加上求积符号来保证函数不变，而不是在求导后结果再加上求导符号。但在考场高度紧张的状态下难免会发生笔误，本身幂级数就很复杂，你再稀里糊涂地加上求导、求积符号，就显得更混乱。为了避免这样的错误，我觉得这样处理更好：

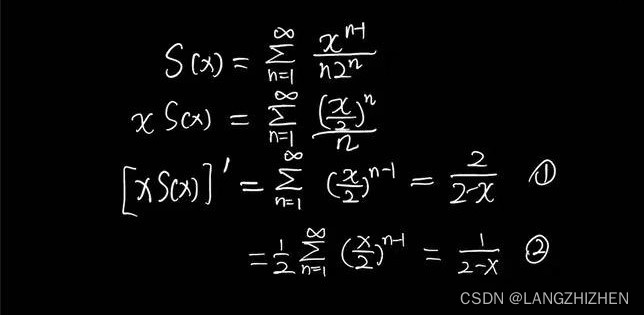
即左边写上S(x)代表和函数，右边写上要处理的幂级数，这样就不需要把求导和求积的步骤强加在幂级数上，而左边很简单，处理起来更方便。而且左右是经过相同的处理，更利于简化思考。

错误三：求导忽略复合函数求导

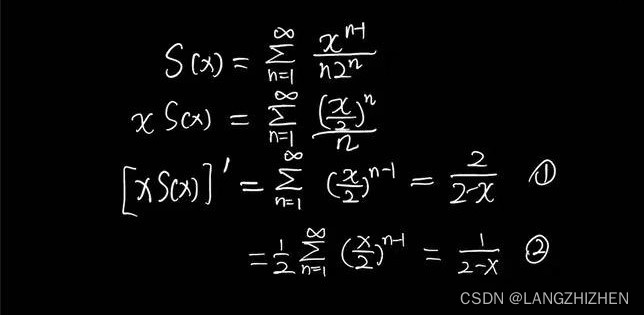
接下来又出现的两种结果。那么哪个正确呢？
The latter, of course~
因为我们在逐项求导的时候，是对x这个变量求导。而此时右端的幂级数是以x/2为变量。所以我们这时候就需要复合函数求导：先对x/2整体求导，x/2再对x求导

错误四：求积忽略变上限积分

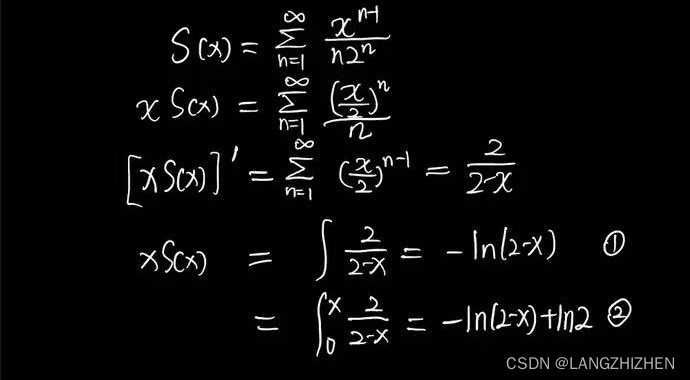
还是这张图，在逐项求积分以后，我们出现了两种结果，哪一个正确呢？It is clear that the latter is true~
有的小伙伴可能一直有疑惑，为什么这里求积分是一个从0
到x的变上限积分而不是一个不定积分呢？首先，考试中一个幂级数的和函数一定是唯一的，如果是求得一个不定积分，那还需要加上一个常数C。而和函数的结果会随着C的不同而不同，这不就与和函数唯一相矛盾吗？
其次，为什么下限选取0？第一，大部分情况下，S(0)=0，所以求出来的结果是最简单的，这也就是为什么大部分情况下我们忽略进行变上限积分而没有导致结果错误的原因。第二，由阿贝尔定理可以知道幂级数的收敛域是以原点为中心的对称区间。当x∈收敛域[-R,R]时， 在[0,x]中幂级数的每一项总是连续的，满足逐项积分的条件。详情可以参考这篇文章➡关于幂级数逐项积分的积分下限的讨论

即使当收敛半径为0，x=0仍在收敛域内。所以x=0这个点是恒在收敛域内的。

错误五：结果没有分区间

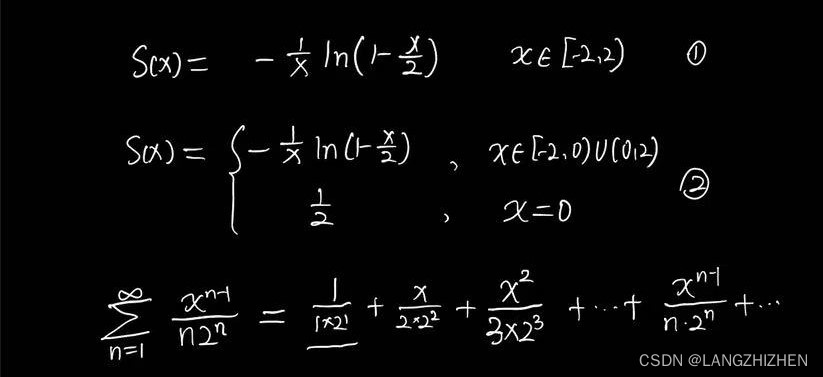
最后我们终于走到了最后一步：写结果了。很多人写法就如同①，真的很可惜。
我们观察到S(x)中有x在分母上，而收敛域中包含了x=0这个点，那么就说明S(x)这个函数在该收敛域中不完全有定义呀，还怎么收敛呢？所以我们需要改一改这个收敛域，即把没有定义的x=0单独抬出来。
有的人会觉得当x=0时整个级数为0，因为幂级数的每一项都有x。哈哈哈哈有点太天真了，不妨我们看一下这个幂级数前几项的构成：
$$\sum _{n=1}^{\infty }\frac{x^{n-1}}{n{2}^n}=\frac{x^0}{1\ast 2}+\frac{x^1}{2\ast 2^2}+\frac{x^2}{3\ast 2^3}+\cdot \cdot \cdot$$
当n=1的时候，第一项是1/2呀跟x无关，所以有时候做题不能想当然，自己觉得是什么就往上写。如果能写出前几项来，那么情况会清晰得多。
所以在我们求出和函数S(x)时，我们需要回头检查这个和函数S(x)在原来收敛域上是否有定义。

总结

这五大错误是我最近做题总结出的，考试的时候如果是考察常规解法和过程也就是一个填空题。填空题没有步骤，如果在上述过程中出现一丁点的错误，5分就丢了。所以细节需要重视，再加上一定量的练习，相信一定能掌握。