-
DataStructure篇:RBT(红黑树)
总结于:2023王道考研
一、红黑树设计及性质
1.1、为什么设计红黑树?
从理论上分析,平衡二叉树的效率已经足够高了,那为什么还需要设计红黑树呢,诶,问题就出在平衡二叉树的严格要求上面,这个严格要求就是
平衡二叉树的任何一颗树结点的左右子树高度差不能超过 1,我们知道,想要维护这个要求是需要付出不小的开销代价的,比如平衡二叉树的插入操作与删除操作都很容易破坏这种平衡特性,导致的结果就是需要频繁调整树的高度,这部分的开销还是不小的,由此,红黑树诞生了。而
红黑树的插入与删除操作大部分时候都不会破红黑特性,也不需要像AVL树一样频繁调整树的高度与形态,即使需要调整,一般都可以在常数级时间内完成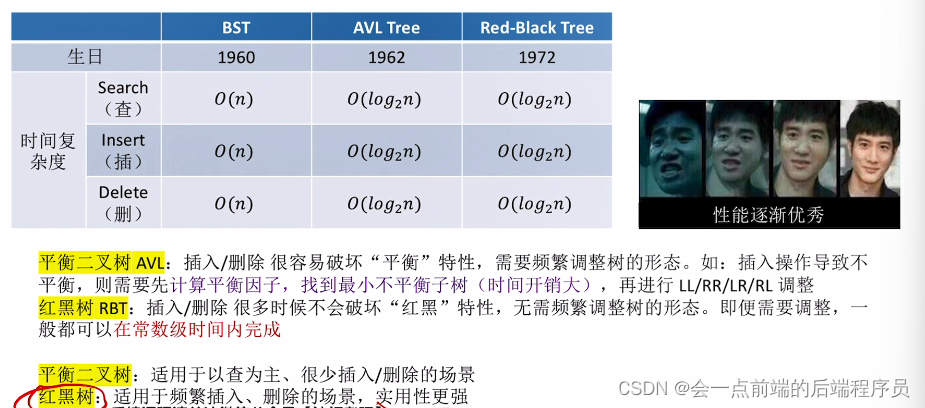
1.2、红黑树会怎么考?(针对考研学生)
🔥红黑树的
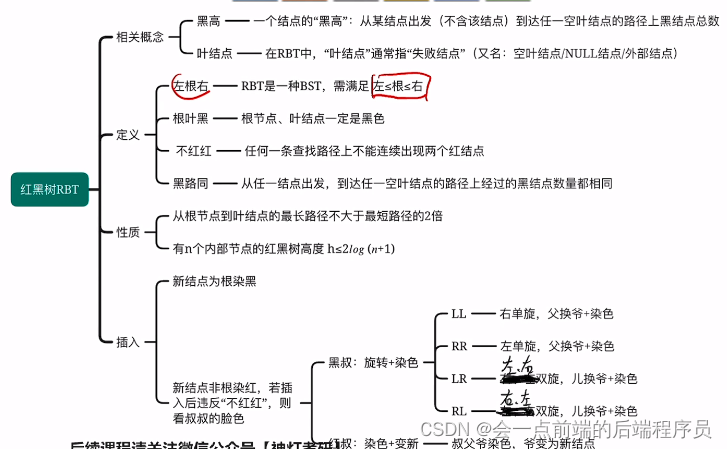
定义、性质——选择题
🔥红黑树的插入/删除——要能手绘插入过程(不太可能考代码,较复杂),删除操作也比较麻烦,也许不考1.3、红黑树的定义
① 包括AVL树的所有定义
② 每个结点不是红色就是黑色
③ 根节点为黑色
④ 叶节点(外部结点,NULL结点,失败结点)均为黑色
⑤ 不存在两个相邻的红结点(既红结点的父节点和孩子结点均为黑结点)
⑥对于每个结点,从该结点到任一叶结点的简单路径上,所含黑结点的数目是相同的struct RBnode{ int key; // 关键值的值 RBnode* parent; // 父结点 RBnode* lChild; // 左结点 RBnode* rChild; // 右结点 int color // 颜色值,0为黑色,1为红色,类似于AVL树的平衡因子 }- 1
- 2
- 3
- 4
- 5
- 6
- 7
来张图看看红黑树,对比上面的定义来看最佳😄
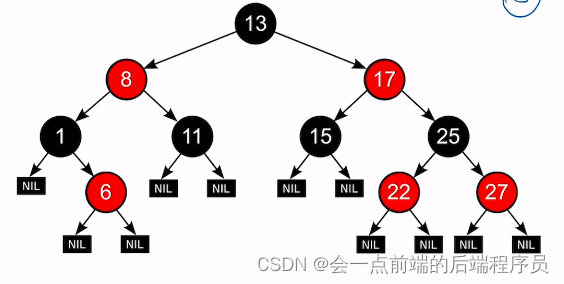
下面来做一个小练习吧,判断下面的树是否符合红黑树的要求

很明显破坏了
相邻结点不都为红色的要求,所以不是红黑树再来一个例子
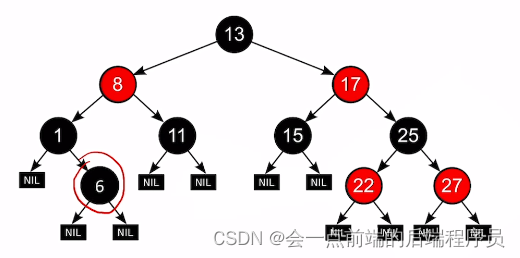
很明显破坏了
对于每个结点,从该结点到任一叶结点的简单路径上,所含黑结点的数目是相同的的要求,所以它也不是红黑树
不知道大家观察到了没有,这棵树不仅不满足上面黑色结点数目要求,还不满足最基本的二叉排序树要求,上面的结点7小于结点8,但是结点7却在结点8的右边。1.4、补充概念: 结点的"黑高"
结点的黑高bh 表示
从某结点出发(不包含该结点)到任一空叶节点的路径上黑结点总数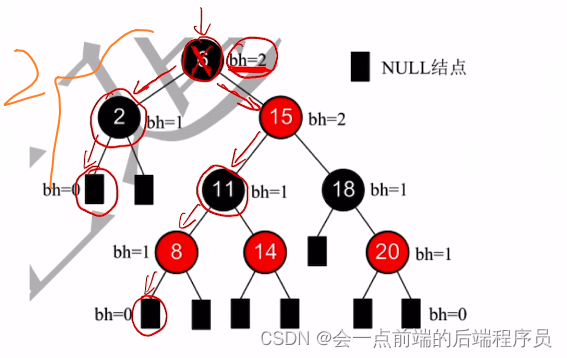
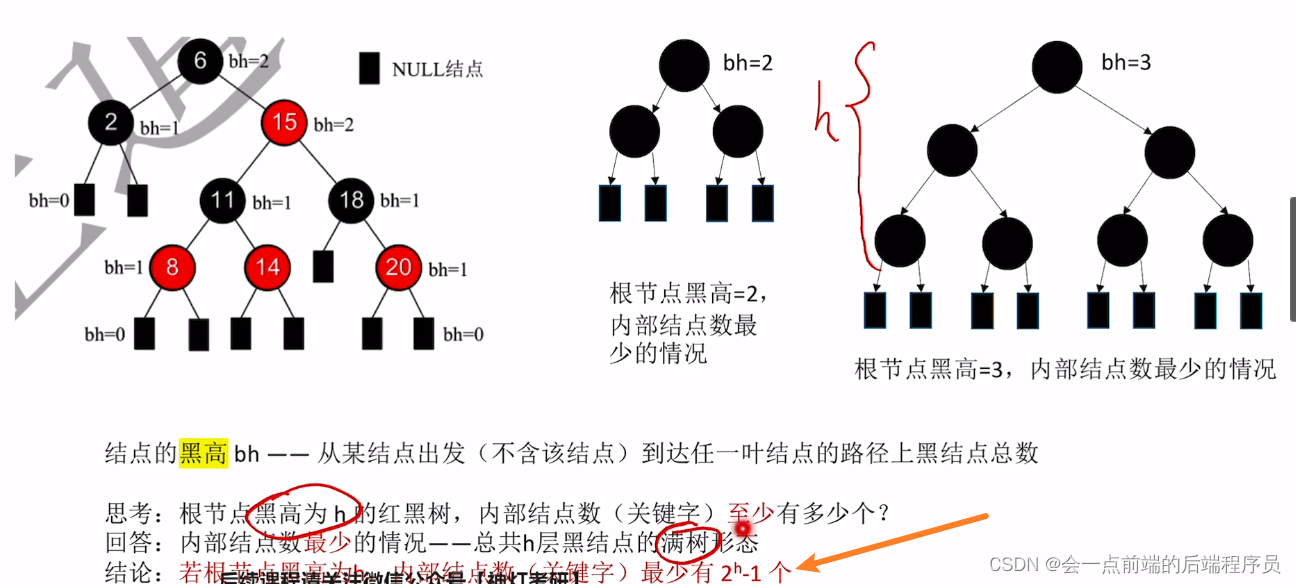

1.5、红黑树的性质
①、从根节点到叶节点的最长路径不大于最短路径的
2倍
②、有n个内部结点的红黑树的高度为 h ⩽ 2 ∗ log 2 ( n + 1 ) h \leqslant 2*\log_2(n+1) h⩽2∗log2(n+1)
③、红黑树的`查找操作时间复杂度 = O ( log 2 n ) =O(\log_2n) =O(log2n) ,与AVL树的查找效率相同二、红黑树的操作
2.1、插入操作
现在我们用一个实际的例子来演示红黑树的插入操作(
建议先复习AVL树的插入操作相关知识)从一颗空的红黑树开始,依次插入:
20, 10, 5, 30, 40, 57, 3, 2, 4, 35, 25, 18, 22, 23, 24, 19, 18先说一下插入的流程(略复杂)

插入根节点20,染成黑色

插入非根节点10,染成红色,原因是需要维持上述红黑树定义的性质六

插入非根节点5,由红黑树的定义可知,插入的位置及应该染的颜色如下
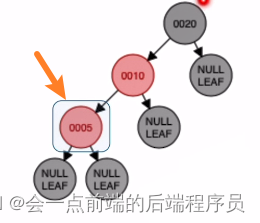
新节点与父节点都是红色,违反了定义五,那要怎么维持红黑树的定义呢很容易判断根节点20的左右子树高度差超过了1,所以对
结点20进行右旋,也就是LL操作
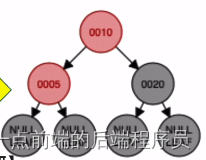
旋转完成后再进行染色操作,结点10位根节点,所以结点10染为黑色,20结点染为红色
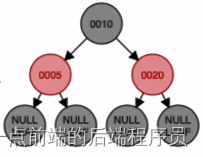
接下来插入结点30,放入如下位置
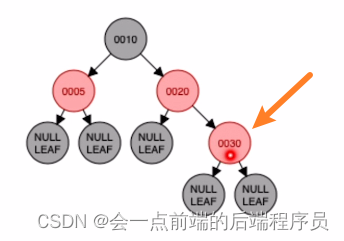
很明显又违反了
定义五,而结点30的叔叔结点是5,并且为红色,所以需要进行将叔父爷颜色逆转,结果如下
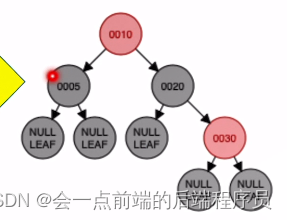
将爷结点当做新插入的结点,而新节点为根节点,所以新节点染成黑色
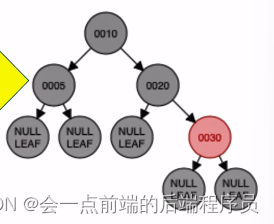
接下来插入结点40,放入如下位置
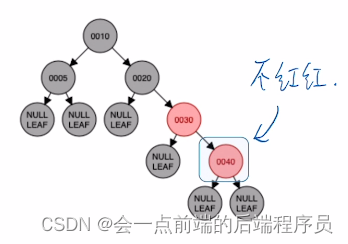
很明显又违反了
定义五,而结点40的叔叔结点是NULL,为黑色,并且为红色,所以需要进行将其叔叔的父节点进行左旋,也就是RR操作,结果如下
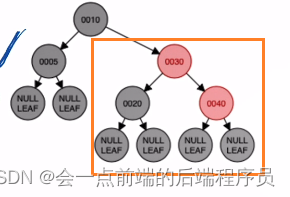
接着进行再进行父叔爷颜色逆转,由于叔叔为NULL,故不需要颜色改变,最终结果如下
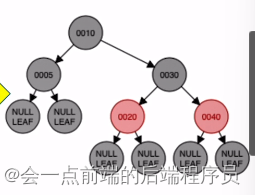
接下来插入结点57,放入如下位置

很明显又违反了
定义五,而结点57的叔叔结点是20,并且为红色,所以需要进行将叔父爷颜色逆转,结果如下,此时平衡了,不需要其他调整
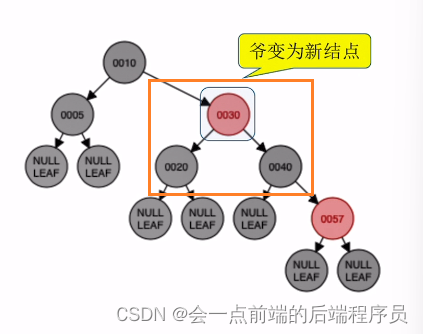
接下来插入结点3,放入如下位置,没毛病,不需要调整
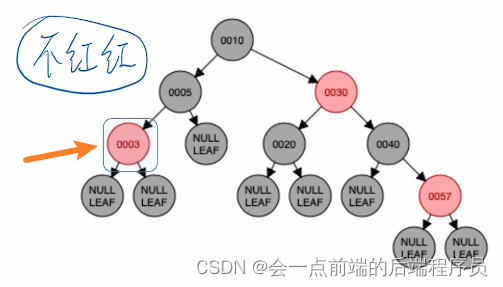
接下来插入结点2,放入如下位置,破坏了平衡很明显又违反了
定义五,而结点2的叔叔结点是NULL,并且为黑色,所以需要进行将其叔叔的父节点进行右旋旋,也就是LL操作,结果如下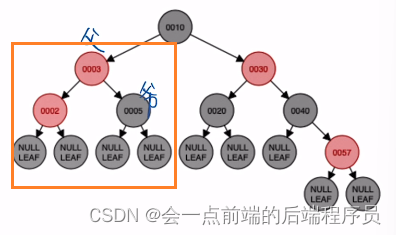
接着进行再进行父叔爷颜色逆转,由于叔叔为NULL,故不需要颜色改变,最终结果如下

接下来插入结点4,放入如下位置,破坏了平衡

很明显又违反了
定义五,而结点4的叔叔结点是2,并且为红色,所以需要进行将叔父爷颜色逆转,结果如下,此时平衡了,不需要其他调整
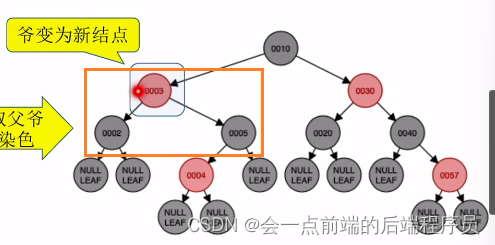
此时红黑树已经平衡接下来插入结点35,放入如下位置,没有破坏平衡
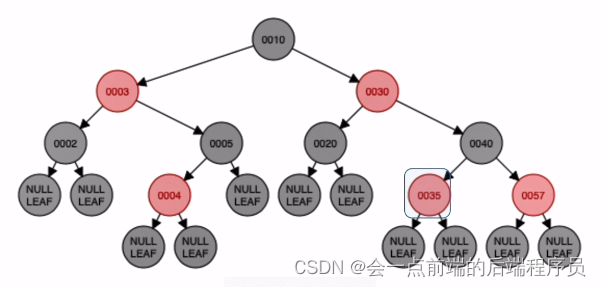
接下来插入结点25,放入如下位置,没有破坏平衡
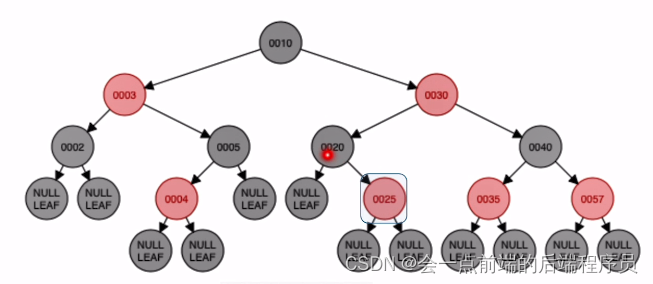
接下来插入结点25,放入如下位置,没有破坏平衡

接下来插入结点22,放入如下位置,破坏了平衡
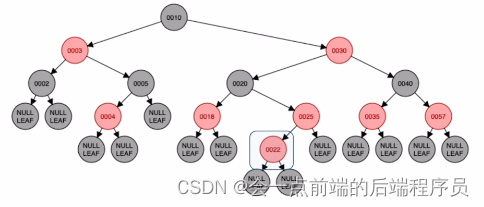
很明显又违反了
定义五,而结点22的叔叔结点是18,并且为红色,所以需要进行将叔父爷颜色逆转,结果如下
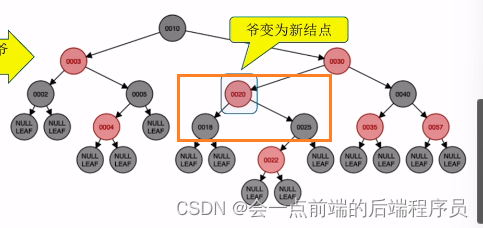
爷结点变成新节点,还是破坏了平衡,继续调整新节点,而新结点20的叔叔结点是3,并且为红色,所以需要进行将叔父爷颜色逆转,结果如下

再次把新节点的爷结点当成新节点,由于此时新节点为根节点,只需要将根节点染为黑色即可
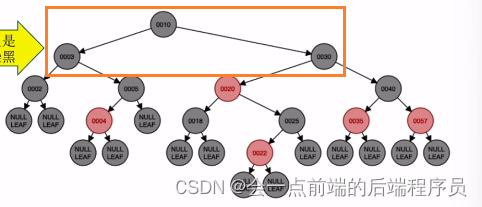
接下来插入结点23,放入如下位置,破坏了平衡

很明显又违反了
定义五,而结点23的叔叔结点是NULL,并且为黑色,并且是因为从黑叔叔的父节点算起,左走,右走到达结点23,所以为LR型旋转,结果如下
先对结点22进行左旋
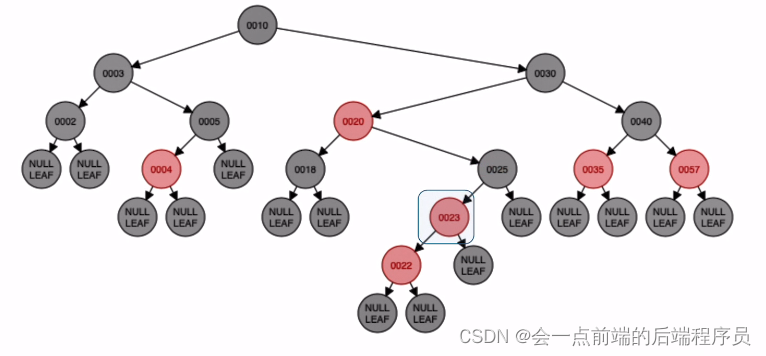
再对结点25进行右旋
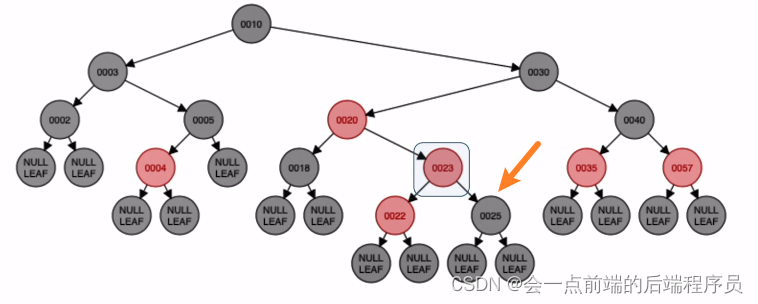
旋转完后,再对原本的儿爷结点进行染色

接下来插入结点24,放入如下位置,破坏了平衡,并且叔叔是红色的,把叔父爷进行染色

染色的结果是

又破坏平衡,叔叔为黑色,考虑旋转了,此时处于LR的位置,如下
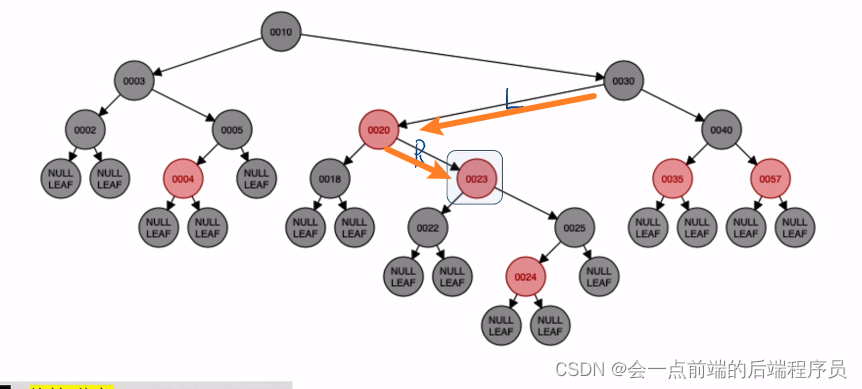
旋转的结果为
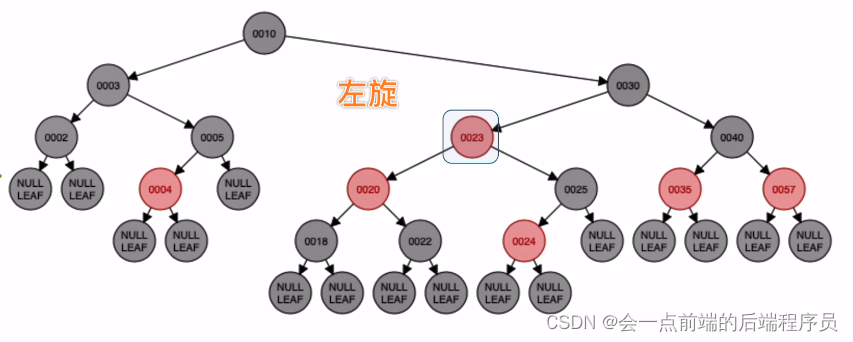
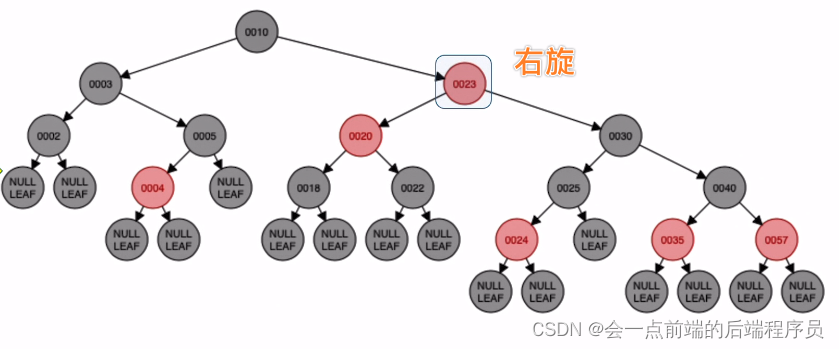
对原本的儿结点与爷结点进行染色即可
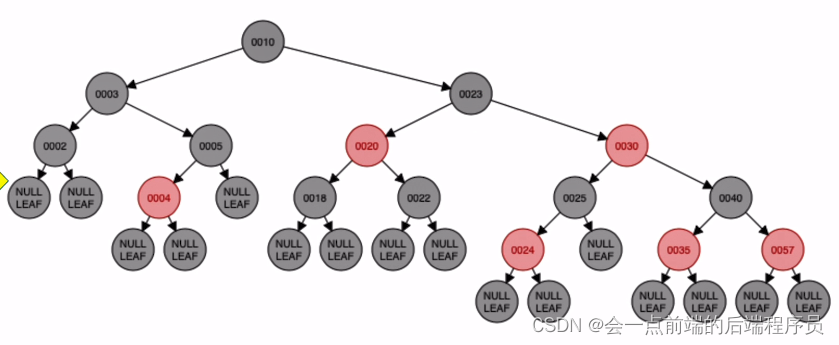
接下来插入结点19,放入如下位置,很nice

接下来插入结点19,放入如下位置,很nice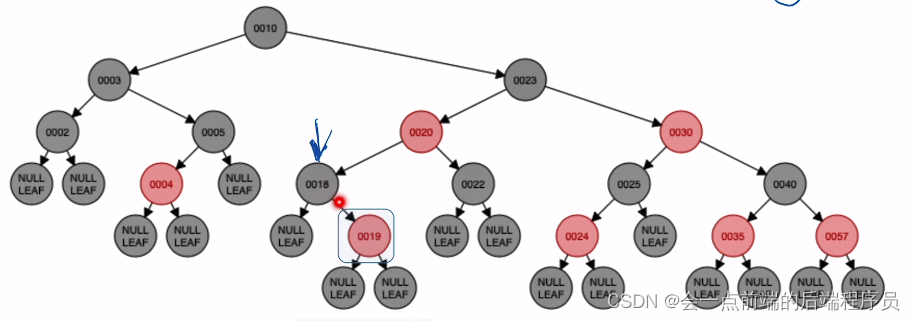
最后插入结点18,你会发现,诶,18已经有了,难道这个新节点18要放弃插入吗,这个18放哪里,看各位读者的意思了,想怎么样就怎么样,这里举例放在19结点的左边
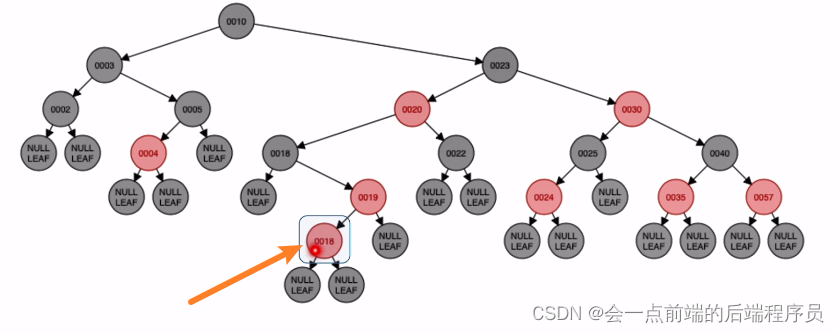
破坏平衡,叔叔结点为NULL为黑色,考虑旋转了,此时处于RL的位置,如下

旋转结果如下
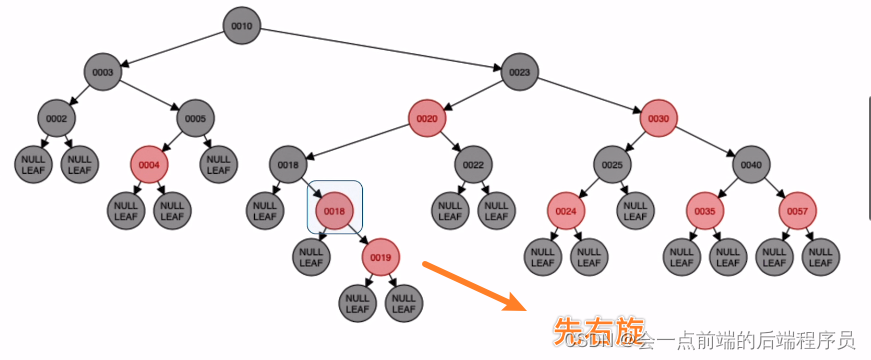
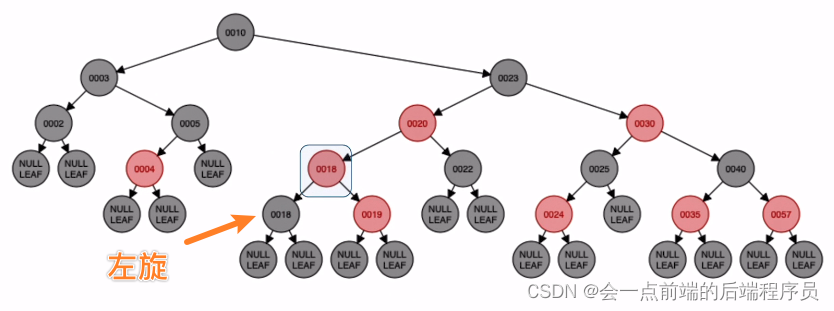
最后对原子爷结点染色,此时就是平衡的红黑树了
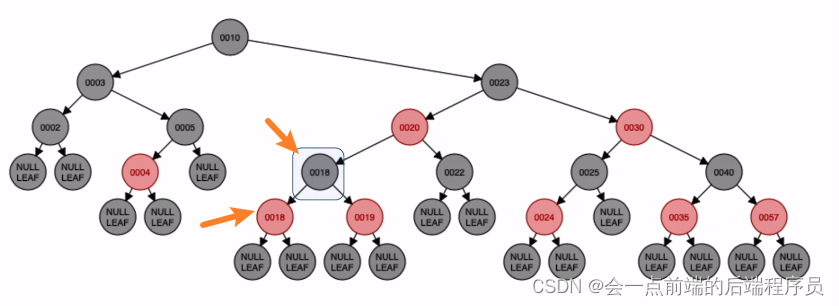
到处为止,终于完成了所有的插入操作了
累死个人了

2.2、删除操作(后续更新…)
-
相关阅读:
流量整形qos
Leetcode之第294场周赛小记
postgresql分组取每组排序后最大最小的两条数据
Node.js 实战 第1章 欢迎进入Node.js 的世界 1.4 Node 自带的工具 1.4.1 npm
QEMU TCG研究
yolo配置(windows)
虚拟化+docker基本概念以及安装部署
服务器老被攻击,该如何解决?
Python:螺旋矩阵与正方形二维列表
神经网络(ANN)
- 原文地址:https://blog.csdn.net/YSJ367635984/article/details/126102348