---

一、插入排序

  插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增1的有序表。

1.基本思想：

  插入排序的工作方式像许多人排序一手扑克牌。开始时，我们的左手为空并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的，原来这些牌是桌子上牌堆中顶部的牌。

2.图解：

3.插入排序的实现：

void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; ++i)
	{
		// [0,end]有序，把end+1位置的值插入，保持有序
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

从第一个元素开始，由于只有一个元素，可认为已经排好了。
接着是第二个，判断第二个元素是否小于前一个元素，满足小于时交换值。
交换值后，用于控制循环的end减小1，被交换的值会与前面的值继续比较，形成有序序列。

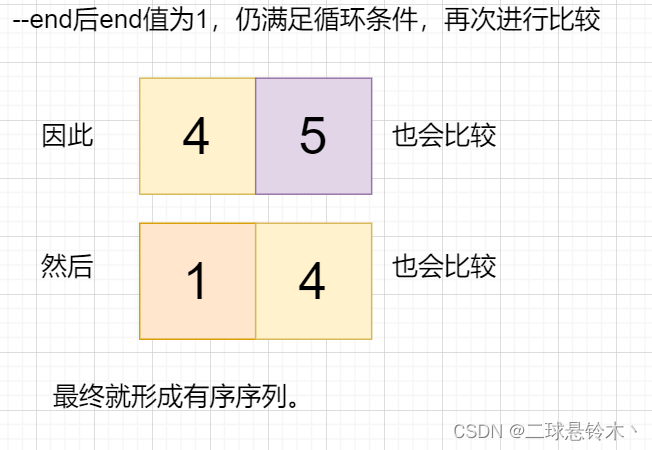
二、希尔排序

  希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因 D.L.Shell 于 1959 年提出而得名。

1.基本思想：

  先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2 =…，继续进行直接插入排序…
  该方法实质上是一种分组插入方法
  比较相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换。算法先将要排序的一组数按某个增量d分成若干组，每组中记录的下标相差d.对每组中全部元素进行排序，然后再用一个较小的增量对它进行分组，在每组中再进行排序。当增量减到1时，整个要排序的数被分成一组，排序完成。

2.图解：

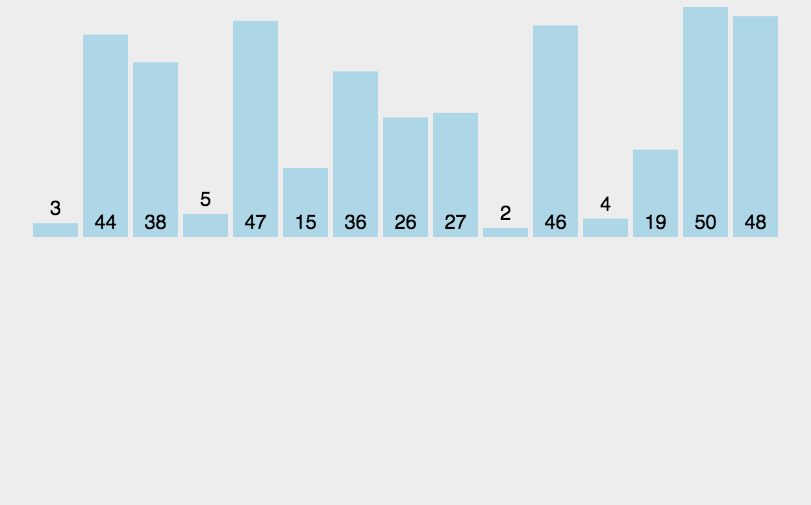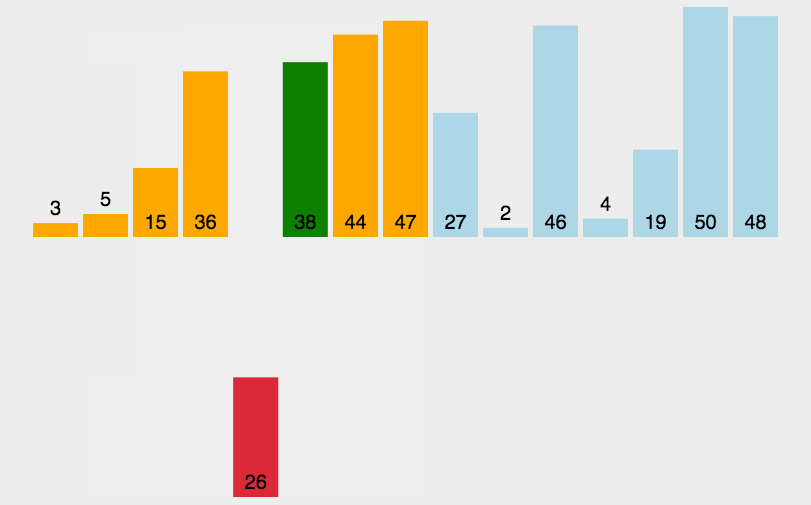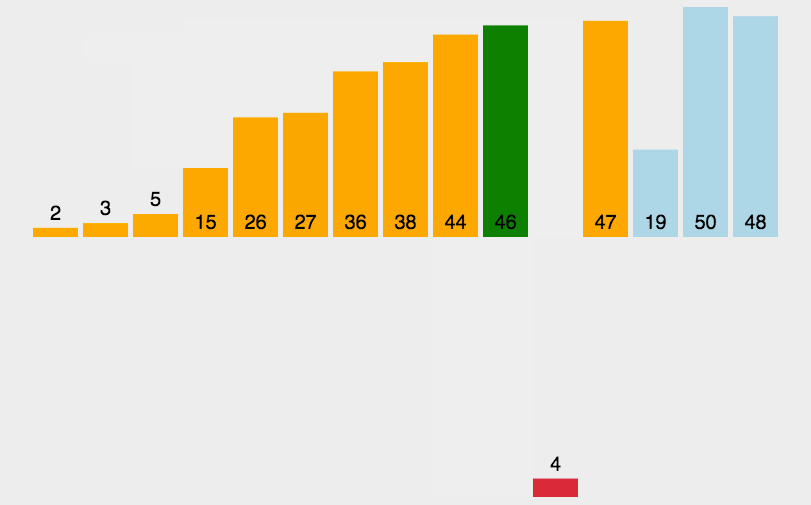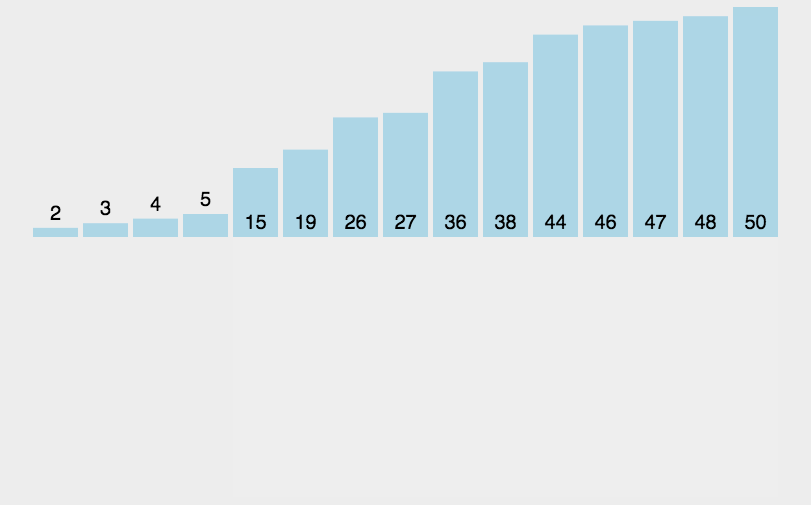
我们取整数d1 = gap = 5作为第一个增量，
图中相同颜色的方块中的数字为同一个组，在一个组内进行插入排序。

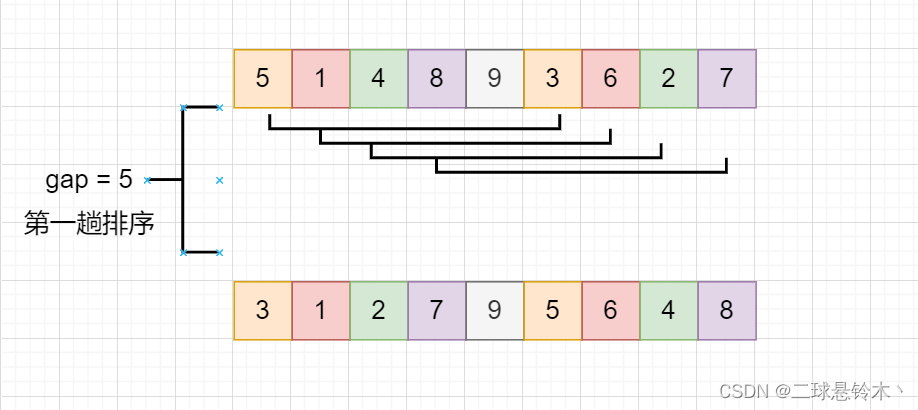
然后缩小gap，取第二个gap = 2，

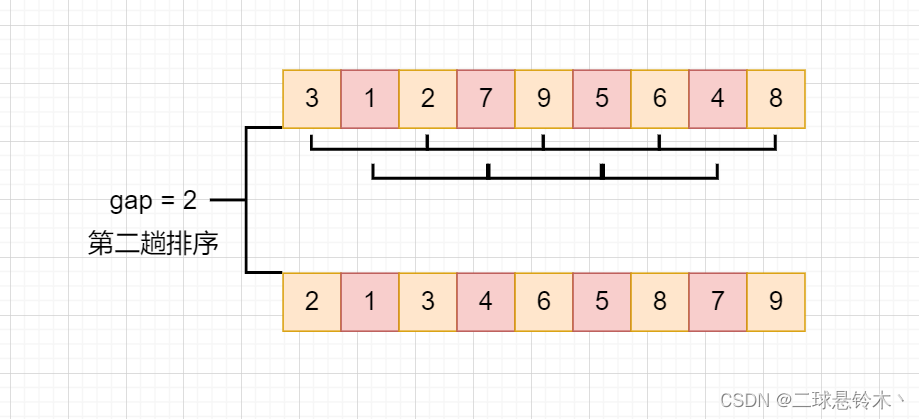
在这里我们可以发现，这个数组明显地变得相对有序。
取gap = 1，

第三趟排序中，gap变成了1，即每个数字单独作为一组，也就是直接插入排序。

由于在插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较N- 1次，时间复杂度为O(N).
由于我们第三躺排序中已经相对有序，大大简化了插入排序的过程。
有人通过大量的实验，给出了较好的结果：当n较大时，时间复杂度大约为O(N^1.3).

3.希尔排序的实现：

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		//gap = gap / 2;

		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

三 、冒泡排序

  由于越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

1.基本思想：

  比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  针对所有的元素重复以上的步骤，除了最后一个。
  持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

2.图解：

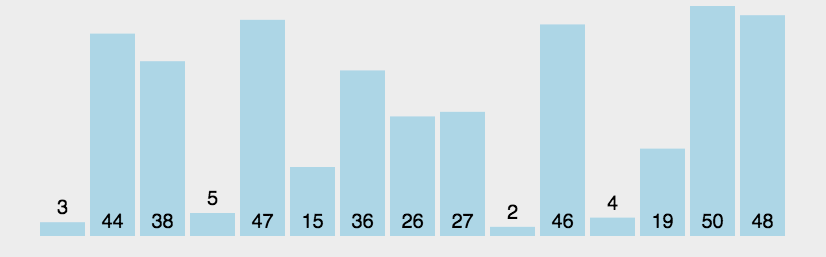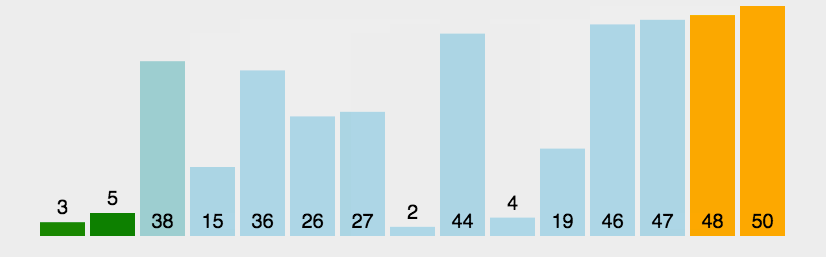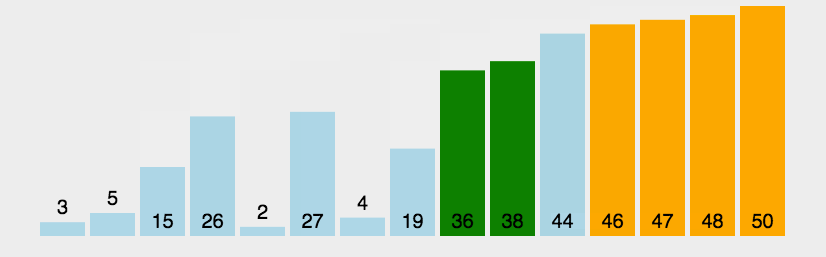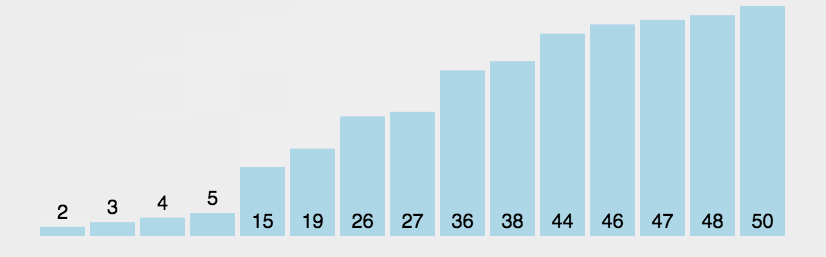
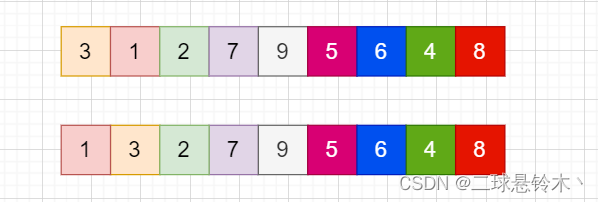
如上图，3和1比较，3大，两者交换。
接着3和2比较，3大，交换。

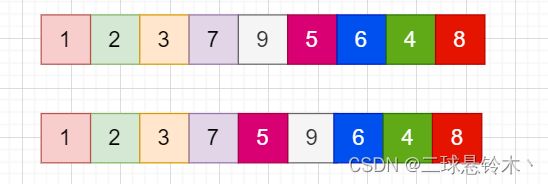
3和7比较，3小，不动。
7和9比较，7小，不动。
9和5比较，9大，交换。
这样一直走下去，第一趟可以形成这个序列：

不断走下去便可像冒泡一样，小的数浮向前面，大的数浮到后面。

3.冒泡排序的实现：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void BubbleSort(int* a, int n)
{
	assert(a);

	for (int j = 0; j < n - 1; ++j)
	{
		int exchange = 0;
		for (int i = 1; i < n - j; ++i)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}

		if (exchange == 0)
		{
			break;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

四、堆排序

  堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

1.基本思想：

  堆排序的过程就是将堆顶元素（最大值或者最小值）与二叉堆的最末尾叶子节点进行调换，不停的调换，直到二叉堆的顺序变成从小到大或者从大到小，也就实现了我们的目的。

  我们这里以最大堆的堆顶元素（最大元素）为例，最后调换的结果就是从小到大排序的结果。

2.图解：

如图，我们创建一个大堆。

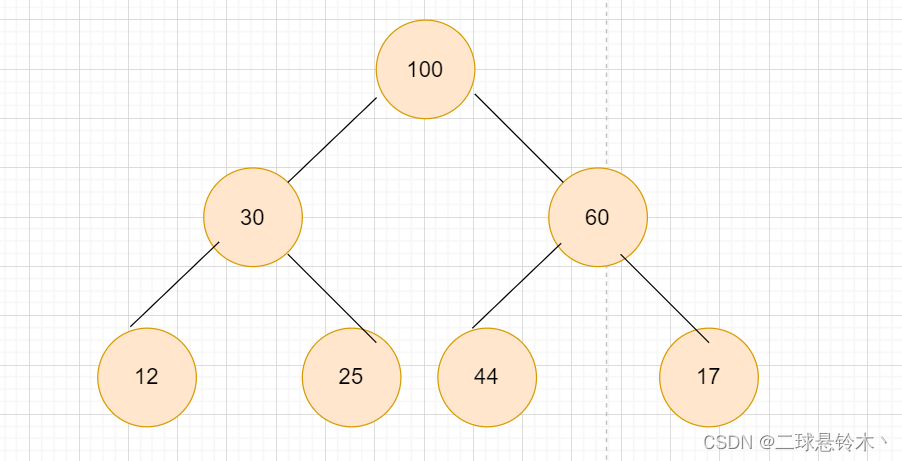
将堆顶元素和堆底元素交换，进行向下调整。

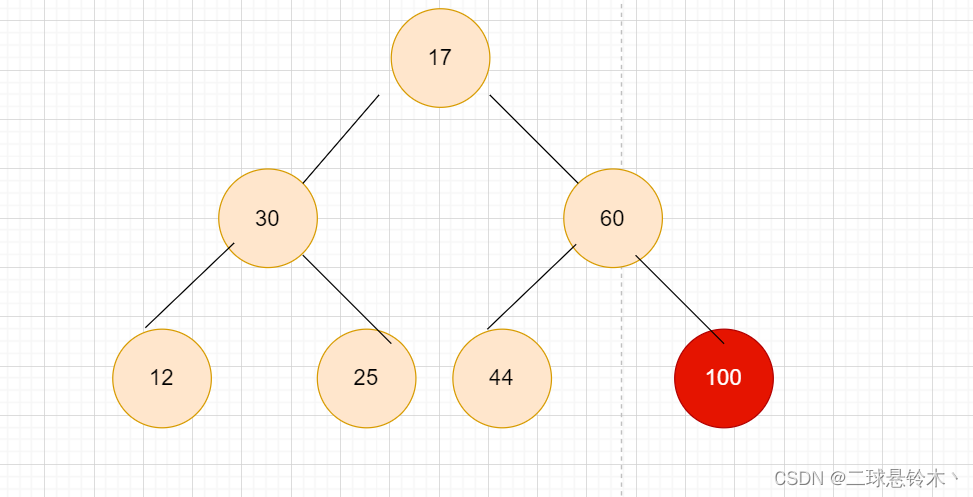
左孩子30代替17的位置

接着25代替17的位置，60代替30的位置，44代替30的位置。

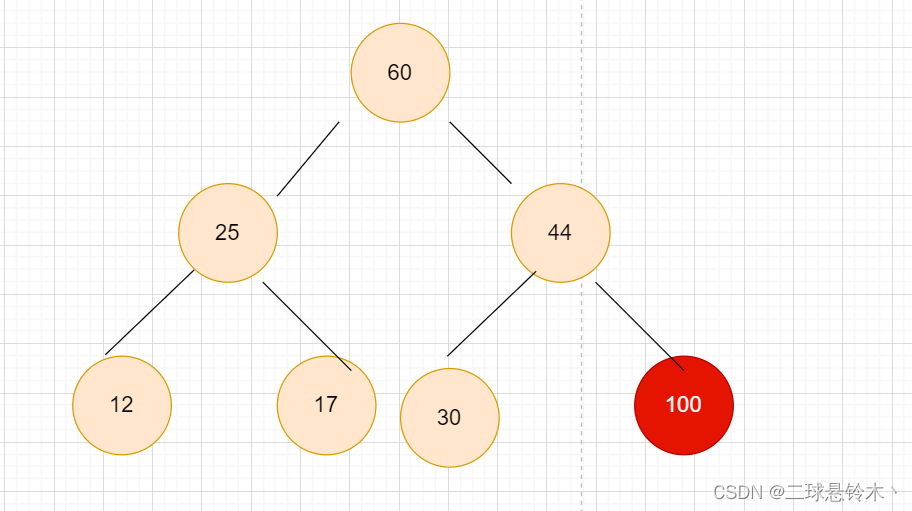
可以发现100沉底后，剩下的数又形成了大堆，继续走下去，60也将沉底，最终形成有序数组。

3.堆排序的实现：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}


void AdjustDwon(int* a, int size, int parent)
{
	int child = parent * 2 + 1;
	while (child < size)
	{
		
		if (child + 1 < size && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

// 降序 -- 建小堆
// 升序 -- 建大堆
void HeapSort(int* a, int n)
{
	// 建堆方式2：O(N)
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDwon(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDwon(a, end, 0);
		--end;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

五、选择排序

1.基本思想：

  每一次从待排序的数据元素中选出最小（或最大）的一个元素，放在序列的起始位置，直到全部待排序的数据元素排完。

2.图解：

该图中即不停地找最小的数，从起始位置开始放。

3.选择排序的实现：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void SelectSort(int* a, int n)
{
	assert(a);
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int mini = begin, maxi = begin;
		for (int i = begin + 1; i <= end; ++i)
		{
			if (a[i] < a[mini])
				mini = i;

			if (a[i] > a[maxi])
				maxi = i;
		}
		Swap(&a[begin], &a[mini]);

		// 如果begin和maxi重叠，那么要修正一下maxi的位置
		if (begin == maxi)
		{
			maxi = mini;
		}

		Swap(&a[end], &a[maxi]);
		++begin;
		--end;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

六、快速排序

  快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右序列重复该过程，直到所有元素都排列在相应位置上为止。

1.基本思想：

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：
(1)首先设定一个分界值，通过该分界值将数组分成左右两部分。
(2)将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于分界值，而右边部分中各元素都大于或等于分界值。
(3)然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

2.图解：

动图很多且会在不经意的时候播放，耐心点哦。

1.Hoare

首先，挑选一个key，一般为最左边或者最右边的值。
右边的小人先走，遇到小于key的值停下，
左边的小人后走，遇到大于key的值停下，
然后两个值交换。
这样下去走到最后，
俩人会相遇，再把key和相遇位置的值交换，
就满足左边的值都小于key，右边的值都大于key。

利用递归，对key左边的序列再次快排，对key右边的序列也快排，最终形成有序序列。

左边做key，右边先走的原因：为了保证相遇位置的值比key小。

2.挖坑法

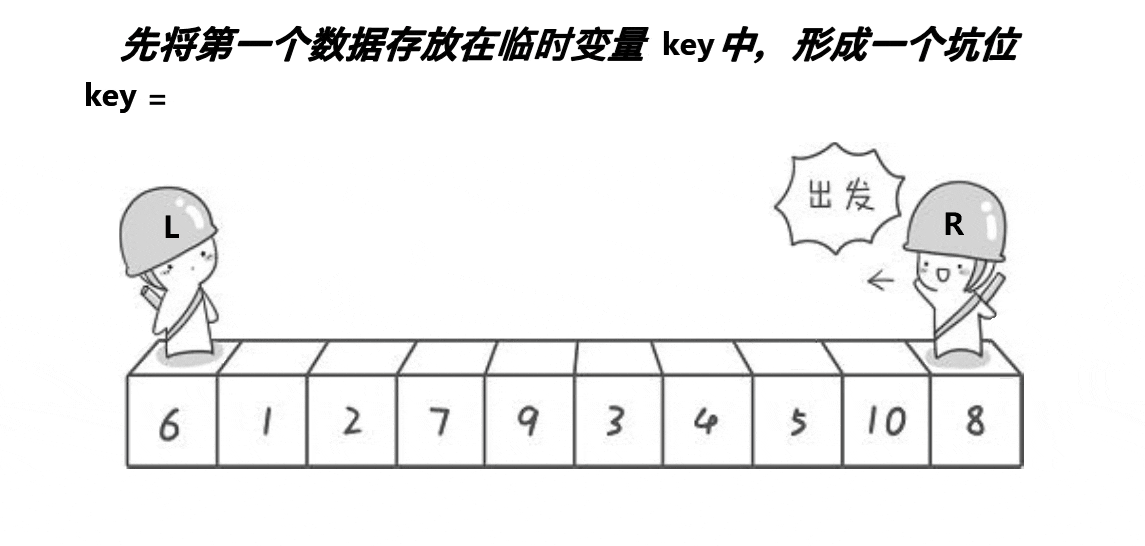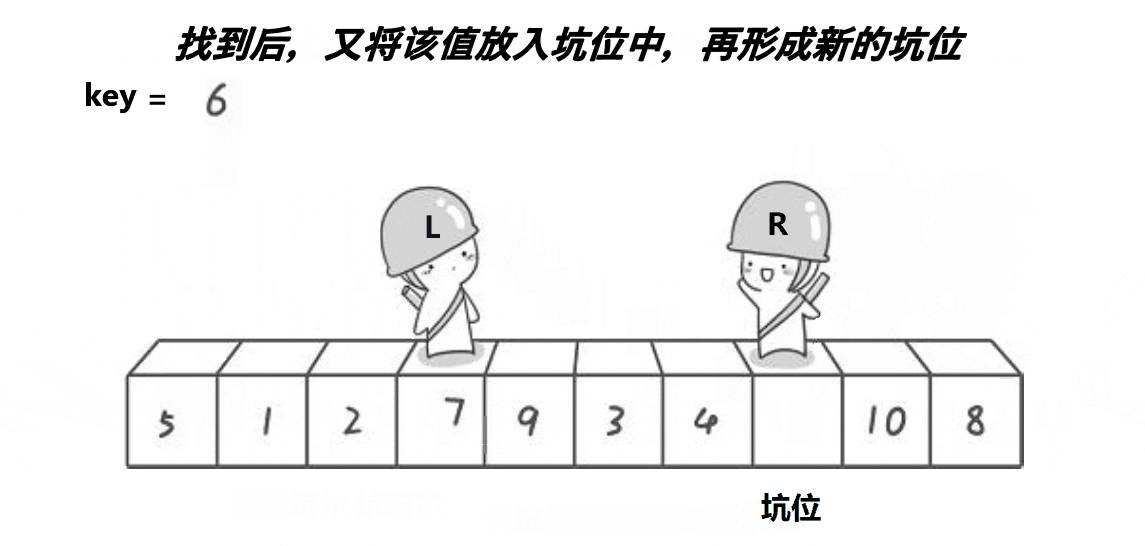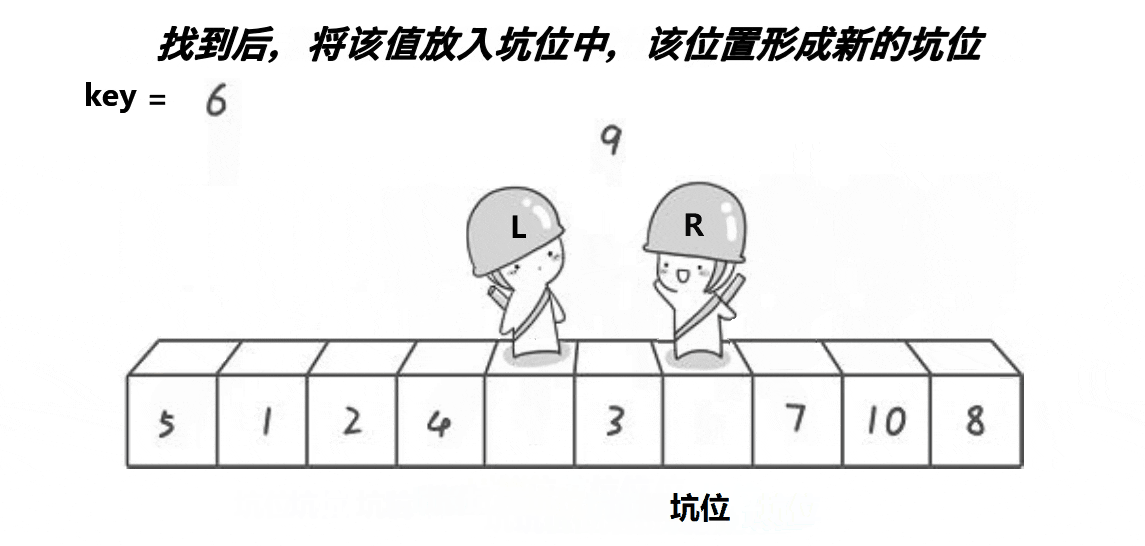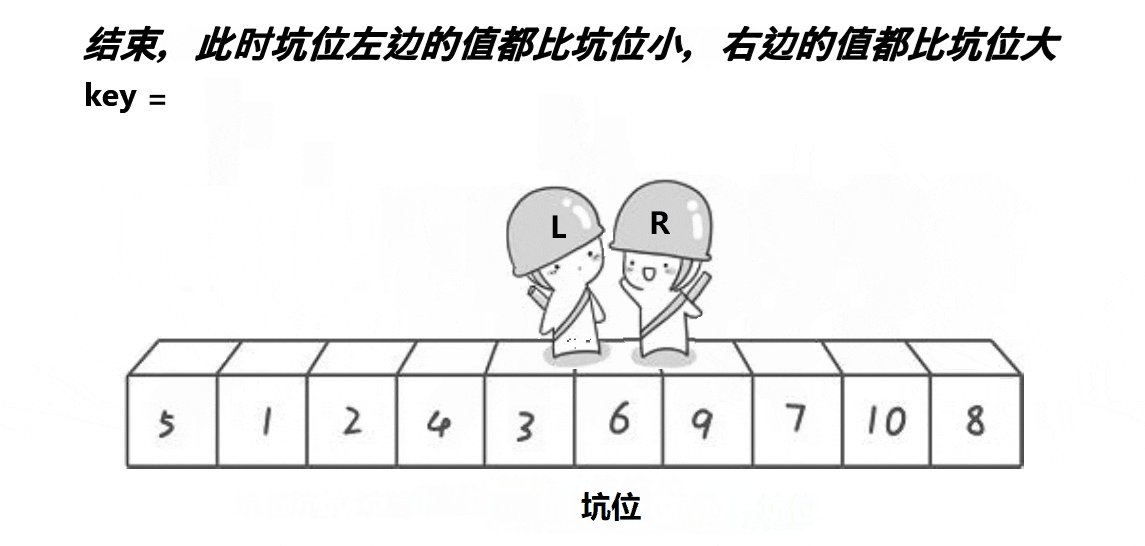
3.前后指针法

3.快速排序的实现：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
 

 //Hoare
int PartSort1(int* a, int begin, int end)
{
	int midindex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midindex]);
 
	int key = a[begin];
	int start = begin;
	while (begin < end)
	{
		// end 找小
		while (begin < end && a[end] >= key)
			--end;
 
		// begin找大
		while (begin < end && a[begin] <= key)
			++begin;
 
		Swap(&a[begin], &a[end]);
	}
  //最后的交换一定要保证a[begin] < a[start], 所以要从右边走
	Swap(&a[begin], &a[start]);
	return begin;
}
 //挖坑法
int PartSort2(int* a, int begin, int end)
{
	//begin是坑
	int key = a[begin];
	while (begin < end)
	{
		while (begin < end && a[end] >= key)
			--end;
 
		// end给begin这个坑，end就变成了新的坑。
		a[begin] = a[end];
 
		while (begin < end && a[begin] <= key)
			++begin;
 
		// end给begin这个坑，begin就变成了新的坑。
		a[end] = a[begin];
	}
 
	a[begin] = key;
 
	return begin;
}
 
 
//前后指针法
int PartSort3(int* a, int begin, int end)
{
	int midindex = GetMidIndex(a, begin, end);
	Swap(&a[begin], &a[midindex]);
 
	int key = a[begin];
	int prev = begin;
	int cur = begin + 1;
 
	while (cur <= end)
	{
		// cur找小，把小的往前翻，大的往后翻
		if (a[cur] < key && ++prev != cur)
			Swap(&a[cur], &a[prev]);
 
		++cur;
	}
 
	Swap(&a[begin], &a[prev]);
 
	return prev;
}

// 三数取中法，三个中取一个中间值
 
int GetMidIndex(int* a, int begin, int end)
{
	int mid = begin + ((end - begin) >> 1);
	if (a[begin] < a[mid])
	{
		if (a[mid] < a[end])
		{
			return mid;
		}
		else if (a[begin] > a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
	else // begin >= mid
	{
		if (a[mid] > a[end])
		{
			return mid;
		}
		else if (a[begin] < a[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
 
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120

七、归并排序

  归并排序是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

1.基本思想：

  设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
  重复步骤，直到某一指针超出序列尾
  将另一序列剩下的所有元素直接复制到合并序列尾

2.图解：

在合并的过程中，

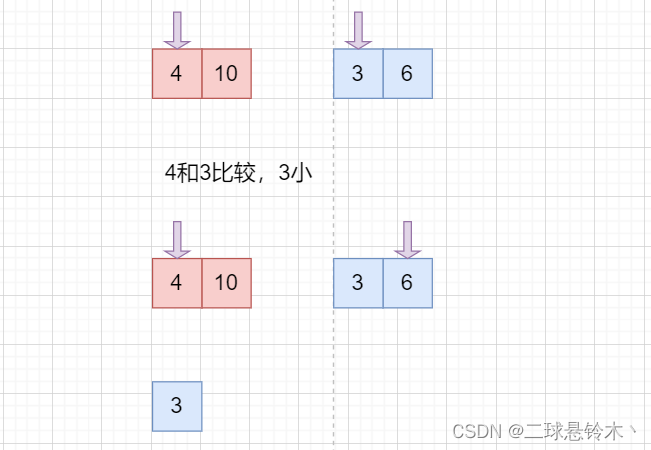
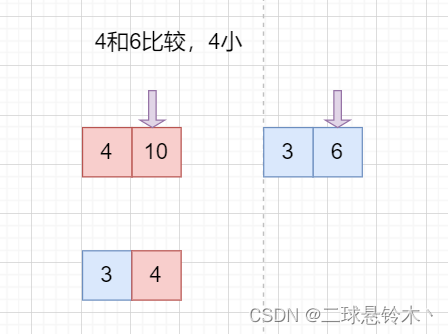
最后就形成3、4、6、10的序列，再和右边形成的数列合并。
最后形成有序序列。

3.归并排序的实现：

//归并排序

void _MergeSort(int* a, int begin, int end,int* tmp)
{
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;

	_MergeSort(a, begin, mid, tmp);
	_MergeSort(a, mid+1, end, tmp);

	//归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1.end2 = end;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}

		//把归并数据拷贝回原数组
		memcpy(a + begin，tmp + begin, (end - begin + 1)*sizeof(int);
	}
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

八、计数排序

  计数排序是一个非基于比较的排序算法,是一种牺牲空间换取时间的做法,它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

1.基本思想：

  1.统计每个数据出现的次数。
  2.按出现的次数写回原数组。
  比方说，1出现2次，2出现6次，0出现3次
  我们就先放3个0，再放2个1，然后放6个2.

2.图解：

3.计数排序的实现：

void CountSort(int* a, int n)
{
	int min = a[0], max = a[0];
	for (int i = 0; i < n; ++i)
	{
		if (a[i]min)
		{
			min = a[i];
		}
		if (a[i] > max)
		{
			max = a[i];
		}
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	memset(count, 0, sizeof(int) * range);

	//统计次数
	for (int i = 0; i < n; i++)
	{
		count[a[i] - min]++;
	}

	//回写排序
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

---

总结

对排序的总结都在这儿了，如有错误劳请斧正。OvO