✨作者介绍：大家好，我是摸鱼王胖嘟嘟，可以叫我小嘟💕
✨作者主页：摸鱼王胖嘟嘟的个人博客主页.🎉
🎈作者的gitee: 小比特_嘟嘟的个人gitee
🎈系列专栏： 【从0到1，漫游c语言的世界】
✨小嘟和大家一起学习，一起进步！尽己所能，写好每一篇博客，沉醉在自己进步的喜悦当中🤭。如果文章有错误，欢迎大家在评论区✏️指正。让我们开始今天的学习吧！😊

💻前言

这篇是对操作符知识的一些补充以及练习！
注：大家可以前去《c语言基础篇：操作符》复习以前知识！

🎈下标引用、函数引用和结构成员

🎉[ ]下标引用操作符

🍁操作符：一个数组名 + 一个索引值

int arr[10];//创建数组
arr[0] = 10;//实用下标引用操作符
1
2

🎉( )函数调用操作符

🍁接受一个或者多个操作符：第一个操作符是函数名，剩余的操作数就是传递给函数的参数。

#include
void test1()
{
	printf("hehe\n");
}
void test2(const char* str)
{
	printf("%s\n",str);
}

int main()
{
	test1();			  //实用()作为函数调用操作符
	test2("hello world.");//实用()作为函数调用操作符
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

🎉访问一个结构的成员

🍁.结构体.成员名
🍁->结构体指针->成员名

#include
struct Stu
{
	char name[10];
	int age;
	char sex[5];
	double score;
};
void set_age1(struct Stu stu)
{
	stu.age = 18;
}
void set_age2(struct Stu* pStu)
{
	pStu->age = 18;//结构成员访问
}
int main()
{
	struct Stu stu;
	struct Stu* pStu = &stu;//结构成员访问
	
	stu.age = 20;//结构成员访问
	set_age1(stu);

	pStu->age = 20;//结构成员访问
	set_age2(pStu);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

🎈表达式求值

🍁表达式求值的顺序一部分是由操作符的优先级和结合性决定。
🍁同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

🎉隐式类型转换

🍁C的整型算术运算总是至少以缺省整型类型的精度来进行的。
🍁为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：

🍁表达式的整型运算要在CPU的相应运算器件内执行， CPU内整型运算器(ALU)的操作数的字节长度
一般就是int的字节长度，同时也是CPU的通用寄存器的长度。
🍁因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
🍁通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

//实例1
char a,b,c;
...
a = b + c;
b和c的值被提升为普通整型，然后再执行加法运算。
加法运算完成之后，结果将被截断，然后再存储于a中。
//负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位：
1111111(截断)
因为 char 为有符号的 char
所以整形提升的时候，高位补充符号位，即为1
提升之后的结果是：
11111111111111111111111111111111
//正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位：
00000001(截断)
因为 char 为有符号的 char
所以整形提升的时候，高位补充符号位，即为0
提升之后的结果是：
00000000000000000000000000000001
//无符号整形提升，高位补0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

整形提升的例子:

#include
int main()
{
	char a = 0xb6;
	short b = 0xb600;
	int c = 0xb6000000;
	if (a == 0xb6)
		printf("a");
	if (b == 0xb600)
		printf("b");
	if (c == 0xb6000000)
		printf("c");
	return 0;
//实例1中的a, b要进行整型提升,但是c不需要整型提升
//a, b整型提升之后,变成了负数,
//所以表达式a == 0xb6,b == 0xb600 的结果是假,
//但是c不发生整型提升,
//则表达式c == 0xb6000000的结果是真
//所以最后输出结果为c
}
//实例2

int main ()
{
 char c = 1 ;
 printf("%u\n" , sizeof(c) ) ;
 printf("%u\n" , sizeof(+c) ) ;
 printf("%u\n" , sizeof(-c) ) ;
 return 0 ;
}
//实例2中的,c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 si zeof(+c) 是4个字节.
//表达式 -c 也会发生整形提升,所以 si zeof(-c) 是4个字节,但是 si zeof(c) ,就是个字节.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

🎉算术转换

🍁如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

long double
double
float
unsigned long int
long int
unsigned int
int
1
2
3
4
5
6
7

🍁如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

警告：但是算术转换要合理，要不然会有一些潜在的问题。

float f = 3.14;
int num = f;//隐式转换,会有精度丢失
1
2

🎉操作符的属性

🍁操作符的优先级：规定了相邻操作符的执行顺序

🍁操作符的结合性：相邻的两个运算符的具有同等优先级时，决定表达式的结合方向，有些需要让表达式从左向右计算（L-R），有些需要从右向左计算(R-L)，还有些并不适用（N/A）

🍁例如：a=b=c中由于前后操作符相同，也就是说优先级相同，而=的结合性为R-L，也就是操作符从右到左执行，相当于a=(b=c)把c赋值给b，然后a=b把b赋值给a，这就是操作符的结合性。

🍁是否控制求值顺序：最具代表性的是逻辑操作符。
例如对于exp1 && exp2的条件，exp1为假时exp2是不会计算的，同样对于exp1 || exp2的条件，exp1为真时exp2也是不会计算的。

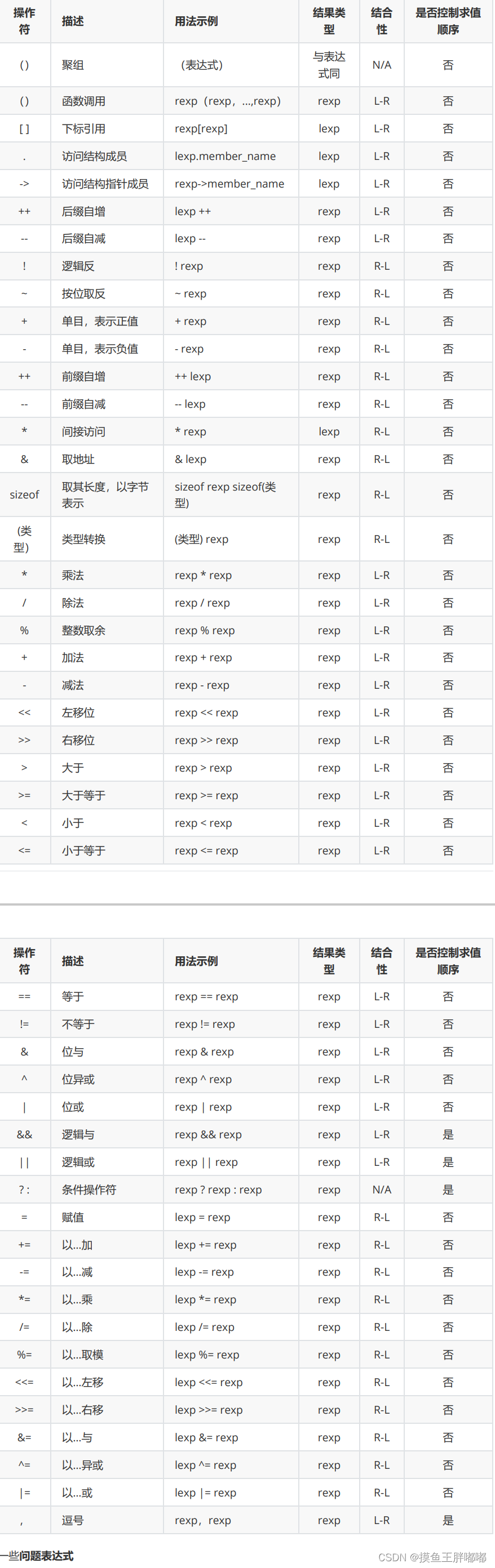
由于操作符的优先级适用于相邻操作符，所以复杂表达式的值在不同的编译器下是不同的。

✏️练习一

问题：
统计二进制中1的个数
写一个函数返回参数二进制中1的个数
比如：15 0000 1111 4个1

#include

/*
方法一：
思路：
循环进行以下操作，直到n被缩减为0：
   1. 用该数据模2，检测其是否能够被2整除
   2. 可以：则该数据对应二进制比特位的最低位一定是0，否则是1，如果是1给计数加1
   3. 如果n不等于0时，继续1
*/
int count_one_bit_way1(int n)
{
	int count = 0;
	while (n)
	{
		if (n % 2 == 1)
			count++;
		n = n / 2;
	}
	return count;
}


/*
上述方法缺陷：进行了大量的取模以及除法运算，取模和除法运算的效率本来就比较低。
方法二思路：
一个int类型的数据，对应的二进制一共有32个比特位，可以采用位运算的方式一位一位的检测，具体如下
*/
int count_one_bit_way2(unsigned int n)
{
	int count = 0;
	int i = 0;
	for (i = 0; i < 32; i++)
	{
		if (((n >> i) & 1) == 1)
			count++;
	}
	return count;
}


	/*
	方法二优点：用位操作代替取模和除法运算，效率稍微比较高
	  缺陷：不论是什么数据，循环都要执行32次

	方法三：
	思路：采用相邻的两个数据进行按位与运算
	举例：
	9999：10 0111 0000 1111                
	第一次循环：n=9999   n=n&(n-1)=9999&9998= 9998
	第二次循环：n=9998   n=n&(n-1)=9998&9997= 9996
	第三次循环：n=9996   n=n&(n-1)=9996&9995= 9992
	第四次循环：n=9992   n=n&(n-1)=9992&9991= 9984
	第五次循环：n=9984   n=n&(n-1)=9984&9983= 9728
	第六次循环：n=9728   n=n&(n-1)=9728&9727= 9216
	第七次循环：n=9216   n=n&(n-1)=9216&9215= 8192
	第八次循环：n=8192   n=n&(n-1)=8192&8191= 0


	可以观察下：此种方式，数据的二进制比特位中有几个1，循环就循环几次，而且中间采用了位运算，处理起来比较高效
	*/
int count_one_bit_way3(int n)
{
	int count = 0;
	while (n)
	{
		n = n & (n - 1);
		count++;
	}
	return count;
}

#include
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = 0;
	ret = count_one_bit_way1(n);
	printf("%d\n", ret);
	ret = count_one_bit_way2(n);
	printf("%d\n", ret);
	ret = count_one_bit_way3(n);
	printf("%d\n", ret);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

✏️练习二

问题：
交换两个变量（不创建临时变量）
不允许创建临时变量，交换两个整数的内容

#include 
int main()
{
    int a = 10;
    int b = 20;
    printf("交换前:a = %d b = %d\n", a, b);
    a = a ^ b;
    b = a ^ b;
    a = a ^ b;
    printf("交换后:a = %d b = %d\n", a, b);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12

✏️练习三

问题：
求两个数二进制中不同位的个数
编程实现：两个int(32位)整数m和n的二进制表达中，有多少个位(bit)不同？
输入例子：
1999 2299
输出例子：7

#include 

/*
思路：
1. 先将m和n进行按位异或，此时m和n相同的二进制比特位清零，不同的二进制比特位为1
2. 统计异或完成后结果的二进制比特位中有多少个1即可
*/
#include 
int calc_diff_bit(int m, int n)
{
	int tmp = m ^ n;
	int count = 0;
	while (tmp)
	{
		tmp = tmp & (tmp - 1);
		count++;
	}
	return count;
}


int main()
{
	int m, n;
	while (scanf("%d %d", &m, &n) == 2)
	{
		printf("%d\n", calc_diff_bit(m, n));
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

✏️练习四

问题：
打印整数二进制的奇数位和偶数位
获取一个整数二进制序列中所有的偶数位和奇数位，分别打印二进制序列

#include 

/*
思路：
1. 提取所有的奇数位，如果该位是1，输出1，是0则输出0
2. 以同样的方式提取偶数位置


 检测num中某一位是0还是1的方式：
   1. 将num向右移动i位
   2. 将移完位之后的结果与1按位与，如果：
	  结果是0，则第i个比特位是0
	  结果是非0，则第i个比特位是1
*/
void Printbit(int num)
{
	for (int i = 31; i >= 1; i -= 2)
	{
		printf("%d ", (num >> i) & 1);
	}
	printf("\n");

	for (int i = 30; i >= 0; i -= 2)
	{
		printf("%d ", (num >> i) & 1);
	}
	printf("\n");
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28