【Leetcode HOT100】不同的二叉搜索树 c++

题目描述：

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

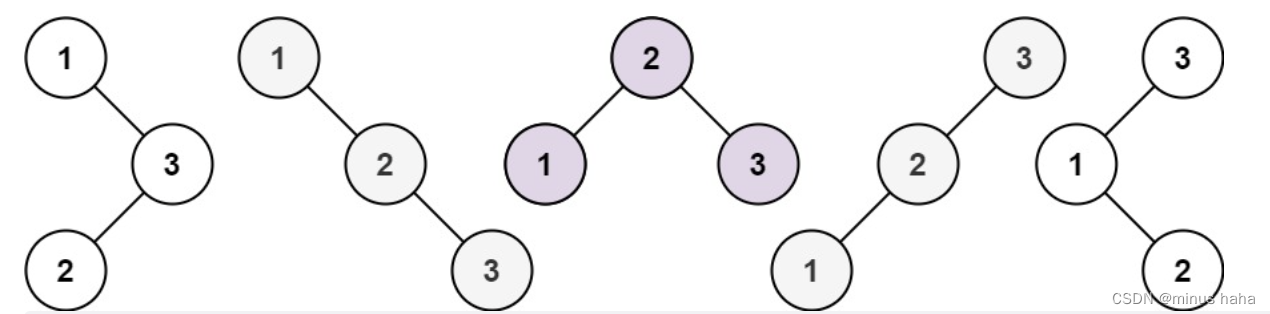
示例 1：

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

1 <= n <= 19

c++代码：

class Solution {
public:
    int numTrees(int n) {
        int dp[n+1];
        dp[0]=1; //空树，只有一种情况
        dp[1]=1;  //只有一个元素，只有一种情况
        for(int i=2;i<=n;i++)dp[i]=0; // 初始化
        for(int i=2;i<=n;i++){ //从2开始计算到n
            for(int j=1;j<=i;j++){ //1～i 依次把每个数当成跟节点,左子树长度为j-1,右子树为i-j
                dp[i] = dp[i] + (dp[j-1]*dp[i-j]); //左子树构建dp[j-1]右子树dp[i-j]
            }
        }
        return dp[n];
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

搜索树的特性是左子树全部小于跟节点，右子树全部大于等于跟节点。

对1～n，每次选取一个数字 i 作为根节点，则可以确定1～i-1是左子树，i+1～n-1是右子树。对于1～i-1，可以继续按照每次选取一个数字 j 作为跟节点划分左右子树的方法，对于i+1～n-1也同样。即可以使用递归。

因为每次选取数字 i 作为根节点时，不同的 i 对应的左右子树有重叠计算的部分，所以可以使用动态规划提高递归的效率。

dp[i]记录长度为i的序列能构成的搜索树个数，遍历1～i，选取j作为根节点，则dp[i]等于每个j作为跟节点时左右子树的个数的累加和，即：
dp[i] = dp[i] + dp[i-1]*dp[i-j]

注意初始化dp[i]=0，因为后面要涉及累加，所以先初始化为0。dp[0]=1,dp[1]=1，初始的两种状态：序列长度为0和为1时，只能构成一种搜索树。

总结：

注意搜索树的特征，左子树小于跟节点，右子树大于等于跟节点。也就是说，一旦确定根节点，即可确定左子树和右子树的范围。

二叉树类问题一半可以递归。首先选取根节点，划分出左右子树。再对左子树和右子树进行同样的处理：选取根节点，然后划分左右子树…可以用动态规划优化递归。

注意左右子树的范围（起始下标和终止下标），可以作为递归 or 动态规划进行的参数。