⭐️前面的话⭐️

本篇文章介绍来自牛客试题广场的两道题题解，分别为【杨辉三角的变形】和【二叉树的镜像】，展示语言java。

📒博客主页：未见花闻的博客主页
🎉欢迎关注🔎点赞👍收藏⭐️留言📝
📌本文由未见花闻原创，CSDN首发！
📆首发时间：🌴2022年7月31日🌴
✉️坚持和努力一定能换来诗与远方！
💭推荐书籍：📚《算法》，📚《算法导论》
💬参考在线编程网站：🌐牛客网🌐力扣
博主的码云gitee，平常博主写的程序代码都在里面。
博主的github，平常博主写的程序代码都在里面。
🍭作者水平很有限，如果发现错误，一定要及时告知作者哦！感谢感谢！

---

---

---

⭐️杨辉三角的变形⭐️

🔐题目详情

以上三角形的数阵，第一行只有一个数1，以下每行的每个数，是恰好是它上面的数、左上角数和右上角的数，3个数之和（如果不存在某个数，认为该数就是0）。

求第n行第一个偶数出现的位置。如果没有偶数，则输出-1。例如输入3,则输出2，输入4则输出3，输入2则输出-1。

数据范围： 1≤n≤10⁹

输入描述 :

输入一个int整数

输出描述：

输出返回的int值

示例1

输入：

4
1

输出：

3
1

题目详情：杨辉三角的变形

💡解题思路

基本思路： 找规律（使用动态规划模拟超时了）

解题思路1： 利用动态规划求出第n行变形杨辉三角的数据，由于n行数巨大，当n大到一定程度，整型就已经溢出了（不到50就溢出了），由于题目只是让我们判断奇数还是偶数，那直接将每次求的的结果&1，这样得到的结果虽然不是准确的值，但是如果原来计算的数是偶数，那它&1仍然是偶数，并且处理后的数据再次运算不会影响最终结果的奇偶性，毕竟加上0不影响奇偶，取决于加上1的次数，也就是加上原数据是奇数的次数，加上偶数次就是偶数，加上奇数次就是奇数。

我们知道第n行的变形杨辉三角，数据个数是total=2*n-1，那么它最中间的下标为total/2，我们可以从中间数据开始入手，由于每一行值的更新仅仅依赖上一行，所以我们可以使用滚动数组来轮换更新值。

状态定义:
我们申请一个2*total大小的二维数组arr，我们定义arr[i][j]表示在三角形变形杨辉三角中的值&1后的结果，就像下面这样，其中三角形里面的1表示奇数，0表示偶数。

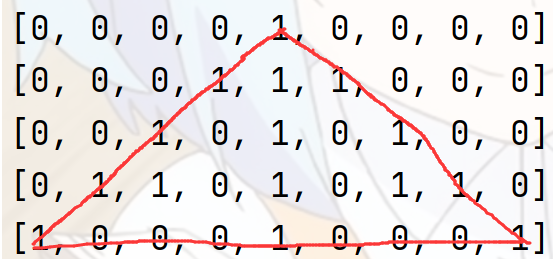
确定初始状态： 一开始只有一行数据时，数组的中点的值为1，即arr[0][total/2] = 1。

状态转移方程： 就如题目所说，满足数组不越界的情况下arr[i&1][j]=(arr[(i-1)&1][j-1]+arr[(i-1)&1][j]+arr[(i-1)&1][j+1])&1，如果获取到上一行数据越界了，就将那一项的值不加，或加上0。

按照上述思路，我们使用动态规划+滚动数组模拟得到第n行的数据奇偶分布，由于我们一开始就已经计算好最后一行的元素个数，并将数组大小设定为该值，所以最终得到的一行数据必定是满的，所以我们不需要区分是越出变形杨辉三角的0还是表示偶数的0，最后我们遍历第n行的数据找到第一个偶数的数组下标加1即可。

由于我们使用了滚动数组，第n行对于二维数组行下标为(n-1)&1，但是由于n可能很大，因此该方案会超时。

解题思路2： 观察变形的杨辉三角，找规律，不妨设行数为n。

当n<3时，没有偶数，输出-1；
当n为奇数时，第一个偶数位置在第二，输出2；
当n为偶数且能被4整除时，第一个偶数位置在第三，输出3；
当n为偶数但不能被4整除时，偶数位置在第四，输出4。

🔑源代码

思路1：动态规划模拟，超时。

import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[][] arr = new int[2][2 * n - 1];
        int total = 2 * n - 1;
        arr[0][total / 2] = 1;

        for (int i = 1; i < n; i++) {
            int cur = i & 1;
            int prev = (i - 1) & 1;
            for (int k = 0; k <= i; k++) {
                int j = total / 2 - k;
                int a = j - 1 >= 0 ? arr[prev][j - 1] : 0;
                int b = arr[prev][j];
                int c = arr[prev][j + 1];

                arr[cur][j] = (a + b + c) & 1;
                j = total / 2  + k;
                a = arr[prev][j - 1];
                b = arr[prev][j];
                c = j + 1 < total ? arr[prev][j + 1] : 0;
                arr[cur][j] = (a + b + c) & 1;
            }
        }
        int lastIndex = (n - 1) & 1;
        for (int j = 0; j < 2 * n - 1; j++) {
            if ((arr[lastIndex][j] & 1) == 0) {
                //System.out.println(arr[lastIndex][j]);
                System.out.println(j + 1);
                return;
            }
        }
        System.out.println(-1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

思路2：找规律。

import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        if (n < 3) {
            //行数小于2，输出2
            System.out.println(-1);
        } else if ((n & 1) == 1) {
            //奇数行输出2
            System.out.println(2);
        } else if ((n & 1) == 0 && n % 4 == 0) {
            //偶数行，且行数可以被4整除，输出3
            System.out.println(3);
        } else {
            //偶数行，且行数不能被4整除，输出4
            System.out.println(4);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

🌱总结

本题为数学运用题，由于数据过大，直接模拟变形杨辉三角会超时，最佳思路是通过观察这个变形杨辉三角的特点总结出每行出现第一个偶数位置的规律。

⭐️二叉树的镜像⭐️

🔐题目详情

操作给定的二叉树，将其变换为源二叉树的镜像。

数据范围：二叉树的节点数 10000≤n≤1000 ， 二叉树每个节点的值 1000 0≤val≤1000

要求： 空间复杂度 O(n) 。本题也有原地操作，即空间复杂度 O(1) 的解法，时间复杂度 O(n)

比如：

源二叉树

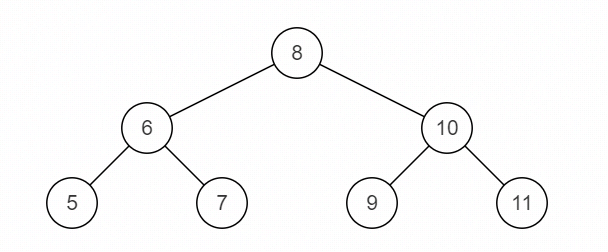
镜像二叉树

示例1

输入

{8,6,10,5,7,9,11}
1

输出

{8,10,6,11,9,7,5}
1

说明

如题面所示    
1

示例2

输入

{}
1

输出

{}
1

题目链接：二叉树的镜像

💡解题思路

基本思路： 前序遍历/中序遍历/后续遍历

解题思路：
我们只需要把所有子树的左右子树全部交换即可。

我们以前序遍历的方式进行左右子树的交换。

第一步，设置递归条件，如果pRoot==null，直接返回。
第二步，交换pRoot的左右子树。
第三步，同样的方式处理左子树。
第四步，同样的方式处理右子树。
第五步，返回pRoot。

这样二叉树就镜像了。

🔑源代码

import java.util.*;

/*
 * public class TreeNode {
 *   int val = 0;
 *   TreeNode left = null;
 *   TreeNode right = null;
 *   public TreeNode(int val) {
 *     this.val = val;
 *   }
 * }
 */

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pRoot TreeNode类 
     * @return TreeNode类
     */
    public TreeNode Mirror (TreeNode pRoot) {
        // write code here
        if (pRoot == null) {
            return pRoot;
        }
        //交换左右子树
        TreeNode tmp = pRoot.left;
        pRoot.left = pRoot.right;
        pRoot.right = tmp;
        //处理左子树
        Mirror(pRoot.left);
        //处理右子树
        Mirror(pRoot.right);
        return pRoot;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

🌱总结

本题为二叉树前中后序遍历应用题，我们只需将所有结点的左右子树交换，就可以得到一颗镜像的二叉树。
类似题：
剑指 Offer 27. 二叉树的镜像
94. 二叉树的中序遍历
145. 二叉树的后序遍历
144. 二叉树的前序遍历

---

觉得文章写得不错的老铁们，点赞评论关注走一波！谢谢啦！