我是目录哦🦥~

一、插入排序🦟

二、希尔排序🦗

三、冒泡排序🦟

四、选择排序🦗

五、堆排序🦟

 六、快速排序🦗

七、归并排序🦟

---

一、插入排序

        排序思想：

        插入排序的思想是把一个待排序数组 arr 分为两个部分，一个部分是有序序列，另一个是无序序列：

        我要从无序序列里拿出一个元素，插入到前面的有序序列中，那么怎么插入呢？
        将从无序序列里拿出的元素 x 和有序序列的最后一个元素 y 进行比较，因为 y 是有序序列里的最后一个元素，所以 y 默认为有序序列里最大的元素。将 x 和 y 比较大小，若 x 大于 y ，那么将 x 安排进这个有序序列，并插入到 y 的后面；如果 x 小于 y ，那么就把 x 和 y 前面一个元素再进行比较，依次往复，直到，x 大于有序序列中的某个元素，插入到那个元素后面；或者 x 小于有序序列的所有元素，那么就插入到有序序列最前面！

        那么我们结合实际例子来看下，我这里有一个待排序数组 arr ：

        我先设定，把数组的第一个元素设为有序序列，因为若数组里只有一个元素，那么他就是有序的。正如上面所说，我要将无序序列第一个元素和有序序列最后一个元素进行比较，那么我们设无序序列第一个元素下标为 i ，有序序列最后一个元素下标为 j ，那么有：

        我们发现，无序序列第一个元素也就是 arr[ i ] ，是大于 arr[ j ] ，的那么就将其插入到后面，这样，有序序列就扩充了一个元素：

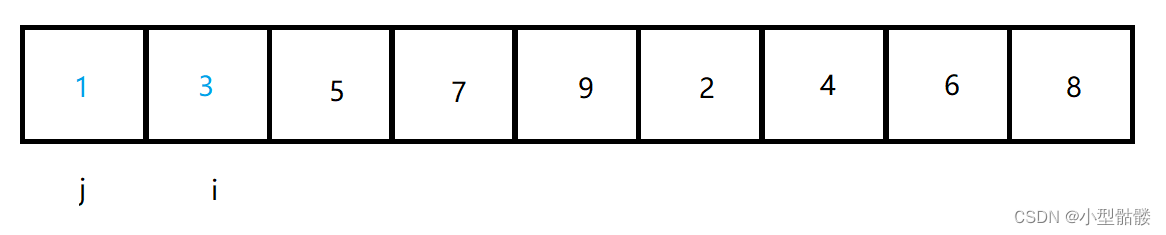
        之后 i 下标继续指向无序序列第一个元素，j 继续指向有序序列最后一个元素：

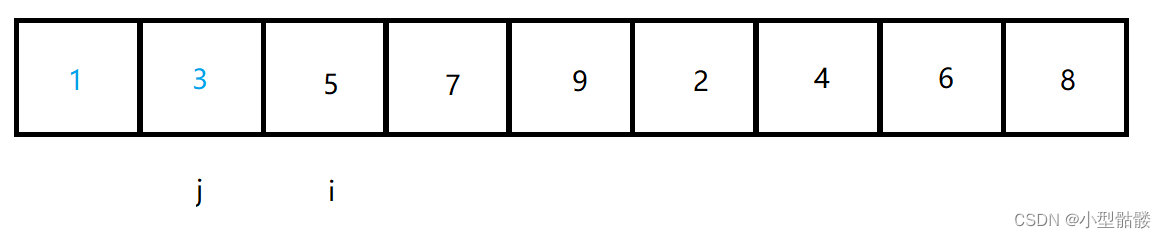
        以此往复，就能把数组排序了。

        代码实现：

public static void insertSort(int[] array){
        // i指向无序序列第一个元素的位置，从1开始
        for (int i = 1; i < array.length; i++) {
            // tmp表示当前待排序的元素
            int tmp = array[i];
            // j指向有序序列最后一个元素
            int j = i - 1;
            // 当j >= 0并且j指向的元素大于tmp时，进入循环
            for ( ;j >= 0 && array[j] > tmp;j--){
                // 令j指向的元素后移一位，以便腾出位置存放tmp
                array[j+1] = array[j];
            }
            array[j+1] = tmp;
        }
    }

        时间复杂度：O(n^2)；空间复杂度：O(1)；稳定性：稳定！

二、希尔排序

        排序思想：

        希尔排序又称缩小增量排序，是插入排序的优化版，为什么是优化版呢？因为经过上面的插入排序，我们知道了时间复杂度为 O(n^2)，即当数组里每一个元素都需要进行排序时，也就是这个数组是以逆序排序时，需要 O(n^2)，那么就意味着当这个数组越趋近于有序，那么时间复杂度越低，最低为 O(n)，即数组已经处于有序状态了。

        所以对于如何优化插入排序我们已经有思路了，那就是使当前数组越趋近有序，时间复杂度越低！

        可是如何使数组越趋近有序呢？先假设现在有一个数组 arr ，它里面存了 10000 个数据，都是逆序状态，那么我们单纯按插入排序来排序，此时就需要将每个数据调整 10000 次，那么总共调整次数为 10000 * 10000 = 1亿 次！
        但是我现在将这 10000 个数据先分个组，我分 100 组，每组包含 100 个数据，这样我先分别对每一组进行插入排序，调整次数就为 1 组 100 次，100 组就有 100 * 100 = 1万 次。之后再对这 100 个有序数组进行插入排序，所以最后的总调整次数就为 100 * 100 * 100 = 100万 次！
        是不是次数顿时就少了很多？相应的，时间复杂度也降低了！

        那么现在问题来了，该怎么分组呢？这里我们一般都是用跳跃式分组，例如一个数组有 15 个数据，分成 5 组，每组 3 个元素，分组模式就为：

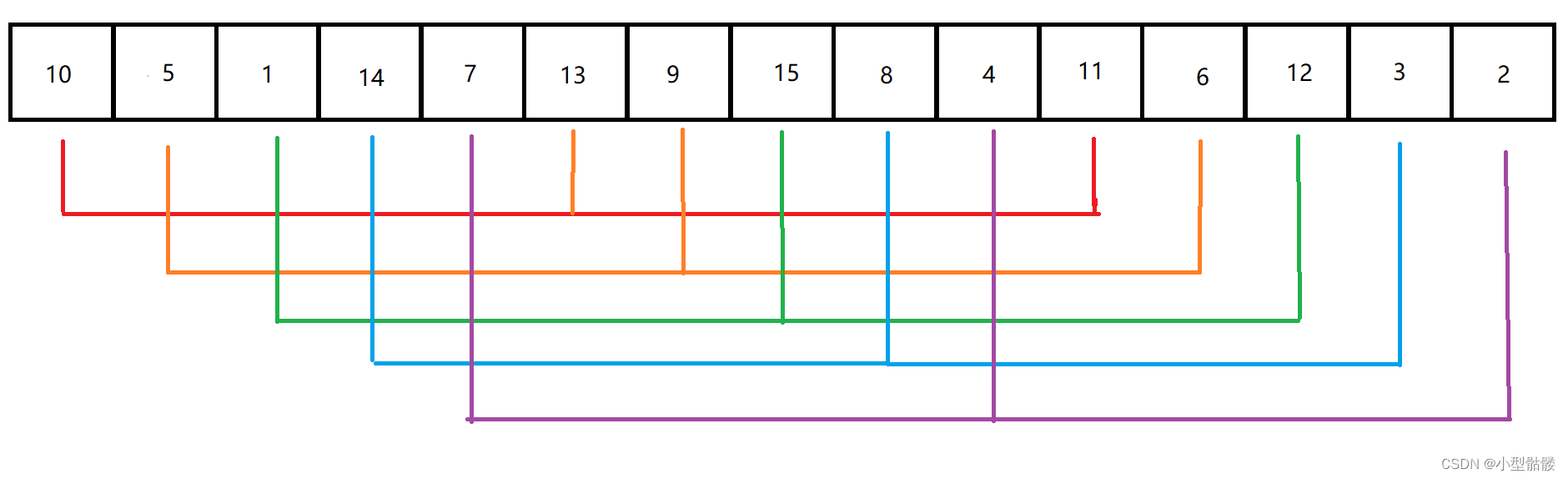
        这种分组方式呢，可以更好更均匀的将数组预排序有序化。之后对于每组排序方式也是和插入排序是一样的，只不过之前是每次往后移动一位，现在是移动组数位，即移动 3 位。

        代码实现：

public static void shellSort(int[] array){
        // g为组数
        int g = array.length;
        // 当组数大于1时，进入循环
        while (g > 1){
            // 每次都对这几组进行插入排序
            insertSortShell(array,g);
            // 每次排序完都使组数缩小，即表示原数组array已经越来越有序
            g /= 2;
        }
        // 以上都是预排序阶段
 
        // 最后才是对array数组真正进行排序，需要保证组数为1
        // 意为不分组，对数组整体进行排序
        insertSortShell(array,1);
    }
    // 希尔排序专用插入排序
    private static void insertSortShell(int[] array, int g) {
        for (int i = g; i < array.length; i++) {
            int tmp = array[i];
            int j = i - g;
            for (;j >= 0 && array[j] > tmp;j -= g){
                array[j+g] = array[j];
            }
            array[j+g] = tmp;
        }
    }

        时间复杂度：O(n^1.3) ~ O(n^1.5)；空间复杂度：O(1)；稳定性：不稳定！

三、冒泡排序

        排序思想：

        在遍历数组时，依次比较相邻两个数的大小，将大数排在后面，小数排在前面；例如在一个数组 arr 里，第一个数大于第二个数，那么就调换这两个数，再和第三个数进行比较，依次往后，就可以在最后得到一个最大的数：

        按照上图，就可以将数组的最大值 6 移动到数组末尾位置，即数组最后一位已经有序了。可是这时候其他元素依然还是无序状态，那么继续循环进行调换，但是这次循环是不应该包含 6 这个元素的，因为它已经有序了！所以循环时应该将终止位置提前一位，若已经有两个元素有序了，那么就把终止位置提前两位。

        但是需要注意的是，如果其中某次调换后数组已经是有序状态了，但是这个循环依然在往后进行，是不是就很浪费了，往后的调换都是在做无用功，所以我么需要在循环前添加一个判断条件：若我们执行完一次循环后，没有任何的元素被调换，那么就说明此时这个数组的所有元素都在它正确的位置上，即数组已经有序了。那么这时候当这个循环结束后，就不该继续往下循环了，尽管还没有全部循环完成。

        代码实现：

public static void bubbleSort1(int[] array){
        // i表示有几个元素处于有序状态，每次进入循环都表示会让一个元素进入有序状态，那么就令i++
        for (int i = 0; i < array.length-1; i++) {
            // flg来表示这个数组的初始状态，开始设为true，表示已经是有序了
            // 如果之后进入循环后发生了元素调换，即表示数组还是无序状态，那么flg = false
            boolean flg = true;
            for (int j = 0; j < array.length-1-i; j++) {
                if (array[j] > array[j+1]){
                    int tmp = array[j];
                    array[j] = array[j+1];
                    array[j+1] = tmp;
                    flg = false;
                }
            }
            // 若经过一次循环后flg依然为true，说明在循环里没有发生调换
            // 即该数组已经是有序状态了，那么退出大循环，程序结束
            if (flg){
                break;
            }
        }
    }

        时间复杂度：O(n^2)；空间复杂度：O(1)；稳定性：稳定！ 

四、选择排序

        排序思想：

        选择排序的思想是以无序序列第一个元素为基准，在后面的无序序列里找出一个最小值，将那个最小值和它调换，这样就可以把一个最小值排到序列的最前面，这样这个序列的第一个元素就是有序的了，再使基准值后移一位，使其始终指向无序序列第一个元素，继续往后调换，直到这个无序序列全部变为有序序列。

        例如一下序列，令 i 指向无序序列第一个元素，j 指向 i+1 ：

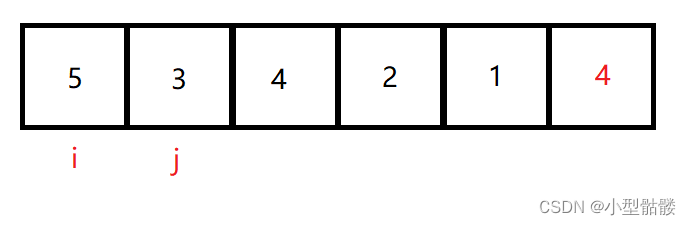
        若 j 指向的值小于 i 指向的值，那么就调换它们，j 往后移动，如果再遇到小于 i 指向的值，继续调换：

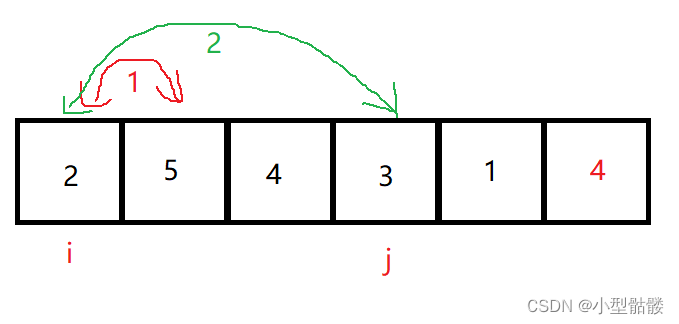
        代码实现：

public static void selectSort(int[] array){
        // i指向无序序列第一个元素
        for (int i = 0; i < array.length; i++) {
            // j从i+1开始，遇到小于i就调换
            for (int j = i+1; j < array.length; j++) {
                if (array[j] < array[i]){
                    int tmp = array[j];
                    array[j] = array[i];
                    array[i] = tmp;
                }
            }
        }
    }

        但是上面的排序有些问题，那就是我们可以发现这个排序算法并不稳定，而且循环时遇到小于的就调换，非常麻烦，那么我们可不可以让它只调换一次，即只和最小的那个数调换呢？答案是可以的！

        在 j 遍历时，维护一个最小值下标 min ，最后循环结束，让 i 和 min 位置的值调换就可以了。

        代码实现：

//优化后的选择排序
    public static void selectSort1(int[] array){
        for (int i = 0; i < array.length; i++) {
            int min = i;// 设置最小值下标
            for (int j = i+1; j < array.length; j++) {
                // 当有元素小于min指向的元素时，更改min的值为j
                if (array[j] < array[min]){
                    min = j;
                }
            }
            // 最后循环结束，将i和min调换元素
            int tmp = array[min];
            array[min] = array[i];
            array[i] = tmp;
        }
    }

五、堆排序

        排序思想：

        堆排序的思想是借助堆的性质：大根堆/小根堆 来实现的，例如大根堆的性质是任意一个节点的左右孩子节点的值都比父亲节点的值小，即根节点的是最大的；小根堆则相反，根是最小的！堆的物理结构是一个队列，而堆的逻辑结构，如下图：

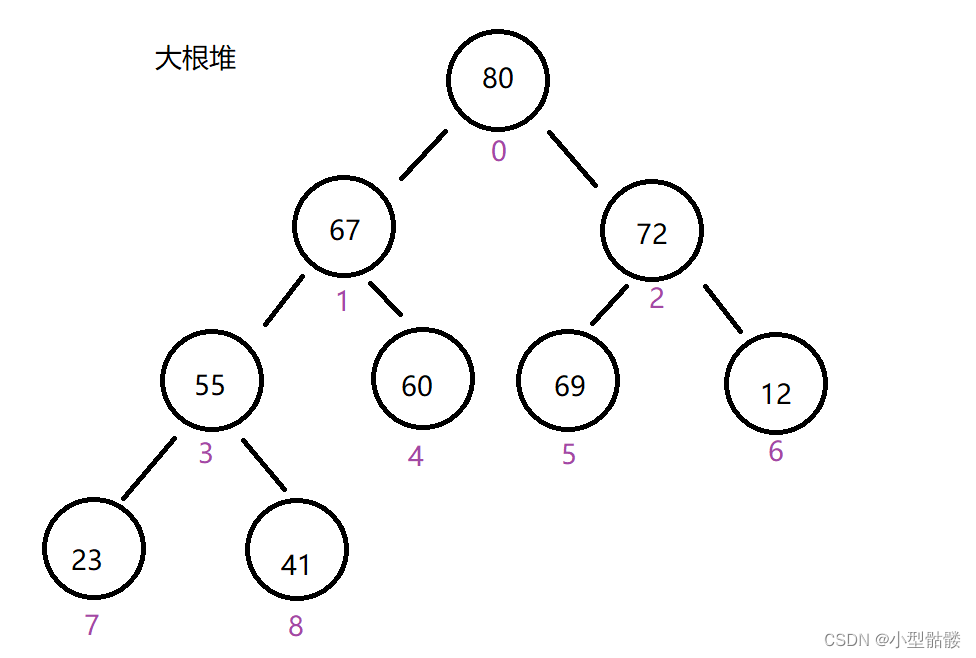
        那么如何利用堆来实现数组的排序呢？我们得先知道升序排序的时候是用大根堆还是小根堆。这里提前告诉大家是用大根堆，那为什么不是小根堆呢？因为堆的物理结构是一个队列，我们只能保证队头的元素一定是堆里最小的元素，之后的元素大小顺序敢保证吗？不敢，因为我们不能区分左孩子节点和右孩子节点的大小顺序！

        那利用大根堆又如何实现数组的升序排序呢？且看：

        当堆处于大根堆情况下，我们使堆首元素和最后一个元素进行调换：

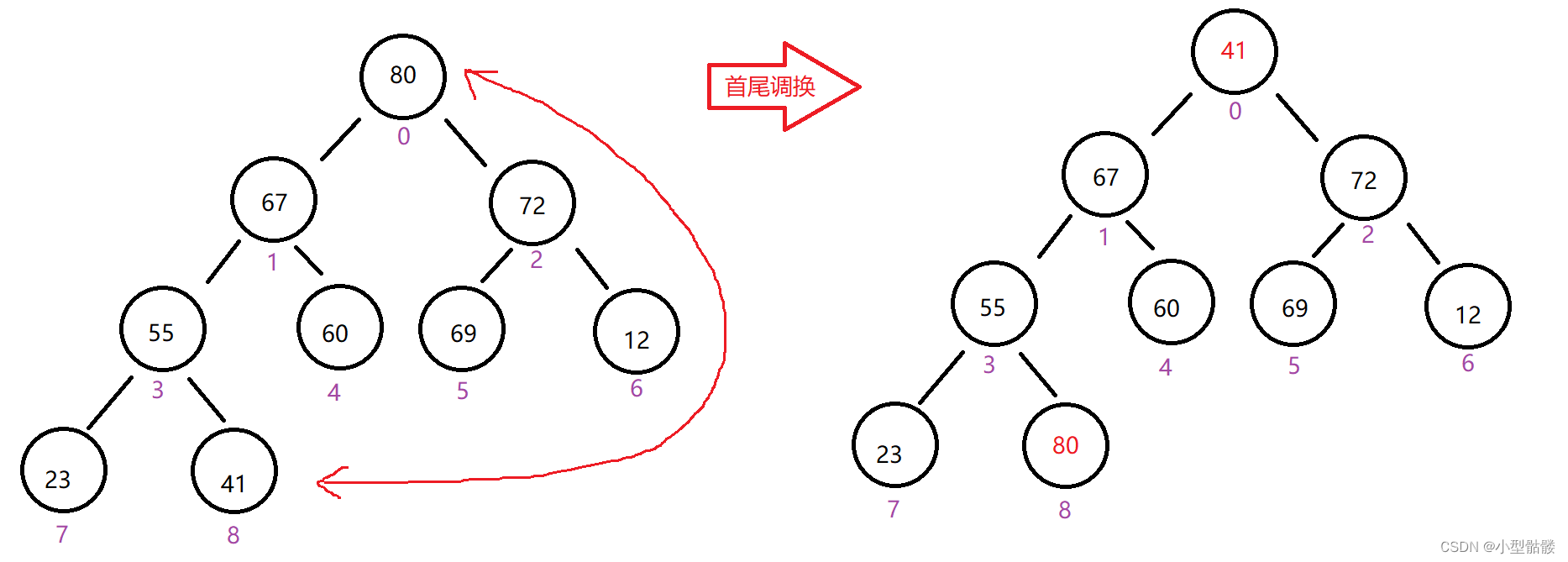
        这样整个数组最大的元素就到了最末尾，然后对这个堆再进行向下调整，只不过这次不算上原始下标为 8 的元素了，即从 0 到 7 进行向下调整，这样原数组最大的元素会保留在堆的最末尾，而经过一次向下调整，还会把下标 0 到 7 的元素的最大值调整到堆首：

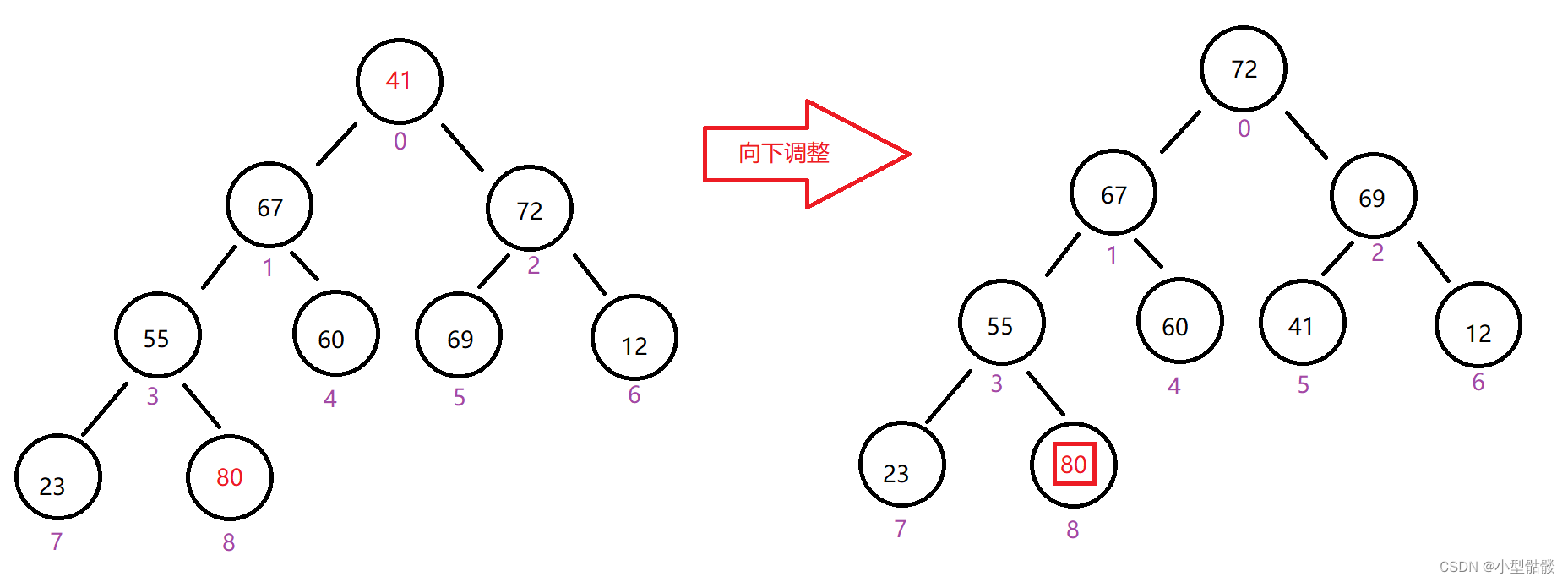
        调整完之后还会循环进行首尾调换：

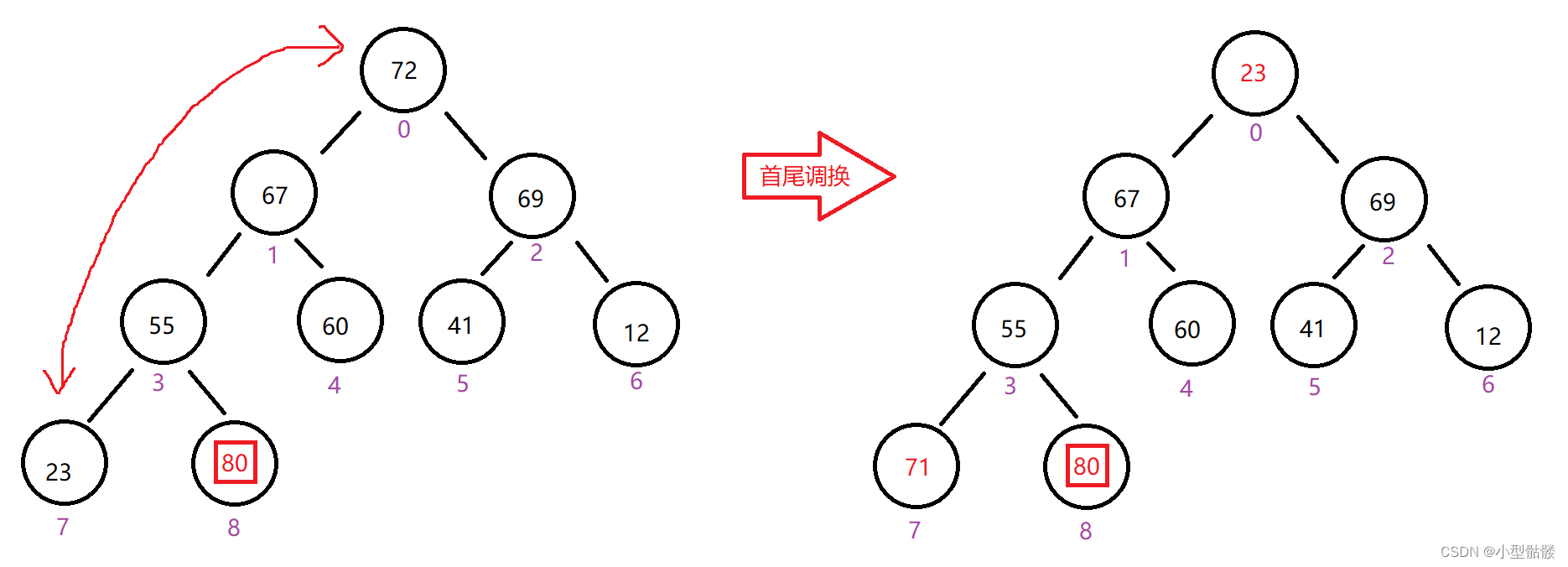
        每次调换后都会使最大值移到数组末尾，而且每次调换完都会让数组的范围缩小，缩小过程是逆序的，就保证了每个父亲节点的左孩子节点一定是比右孩子节点小的，因为每一次右孩子都比左孩子先调换元素，这样就可以保证数组的大小顺序了。当数组范围缩小的 0 时，也就是只剩下最后一个节点需要调换时，循环结束，这样整个数组也就排序完成了。

        代码实现：

public static void heapSort(int[] array){
        createHeap(array); // 创建一个大根堆
        int end = array.length-1; // end指向数组末尾（堆末尾）的元素
        while (end > 0){
            // 先调换堆首元素和堆末尾元素
            int tmp = array[0];
            array[0] = array[end];
            array[end] = tmp;
            // 再从堆首进行向下调整，继续找出新的最大值
            shiftDown(array,0,end);
            // 最后缩小数组范围
            end--;
        }
    }
 
    // 创建一个大根堆
    public static void createHeap(int[] array){
        // 初始将parent指向末尾节点的父节点，从parent开始向下调整
        for (int parent = (array.length-1-1)/2; parent >= 0; parent--) {
            shiftDown(array,parent,array.length);
        }
    }
 
    //向下调整
    public static void shiftDown(int[] array,int parent,int len){
        int child = parent * 2 + 1; // 创建子节点（左孩子）
        while (child < len){
            // 若左孩子节点值小于右孩子，则child指向右孩子
            if (child < len-1 && array[child] < array[child+1]){
                child++;
            }
            // 当子节点值大于父节点时，调换它们的值
            if (array[child] > array[parent]) {
                int tmp = array[child];
                array[child] = array[parent];
                array[parent] = tmp;
                // 调换完后父节点变成子节点，向下调整
                parent = child;
                child = parent * 2 + 1;
            }else { // 当子节点小于父节点值时，说明不需要继续调整了，那么就退出循环
                break;
            }
        }
    }

        时间复杂度：O(n * logn) ；空间复杂度：O(1)；稳定性：不稳定！

 六、快速排序

        排序思想：

        快速排序的思想是从待排序序列中选出一个基准值，即基准值的位置的有序的，也就是说基准值的左边应该都是比基准值小的元素，基准值的右边应该都是比基准值大的元素，这样就把原来的待排序区间分成了两个无序区间 + 基准值，然后再对这两个无序区间分别找到它们的基准值，再使用分冶的思想，直到某个无序区间的长度小于等于1时，那么就说明这个区间是有序的了。

        如何找到基准值和其下标（挖坑法）：
        例如：我定义一个 i 和 j 分别指向无序区间的两端，tmp 作为将来的交换中间值。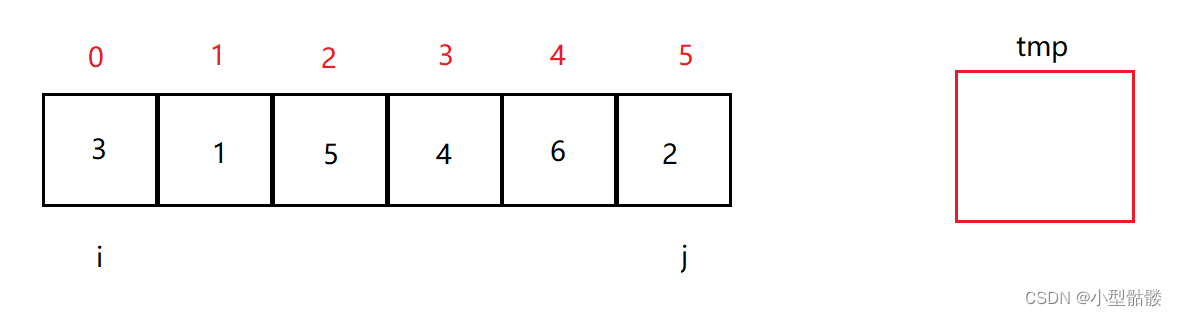

        先将 i 指向的值赋给 tmp，可以看到 i 指向的值“空了”，便成了一个坑；设定此时的这个值为基准值：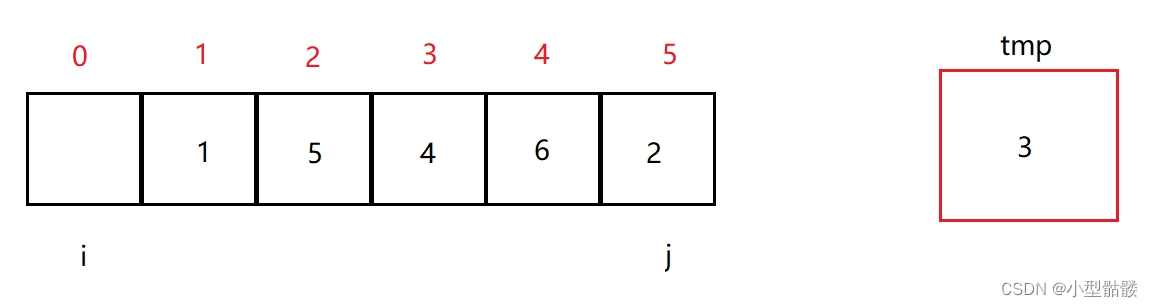

        然后 j 开始往前移动，直到找到小于 tmp 的值，为了放进 i 这个坑里；j 指向的值为2，是小于 tmp 的值的，所以放进 i 的坑内：

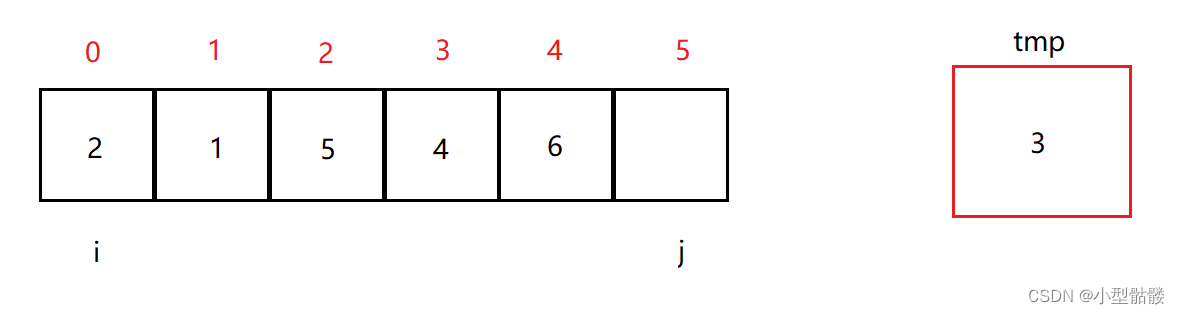
        j 行动完毕后 i 开始继续往后移动，期望找到大于 tmp 的值，放进 j 的坑内；当 i 走到2下标时，值是大于 tmp 的，所以放进 j 里：

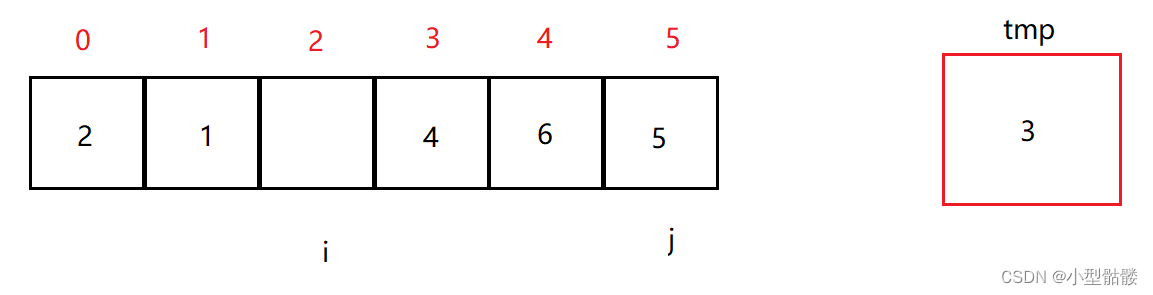
        之后 j 开始往前走，重复上述行为，直到 i 和 j 相遇：

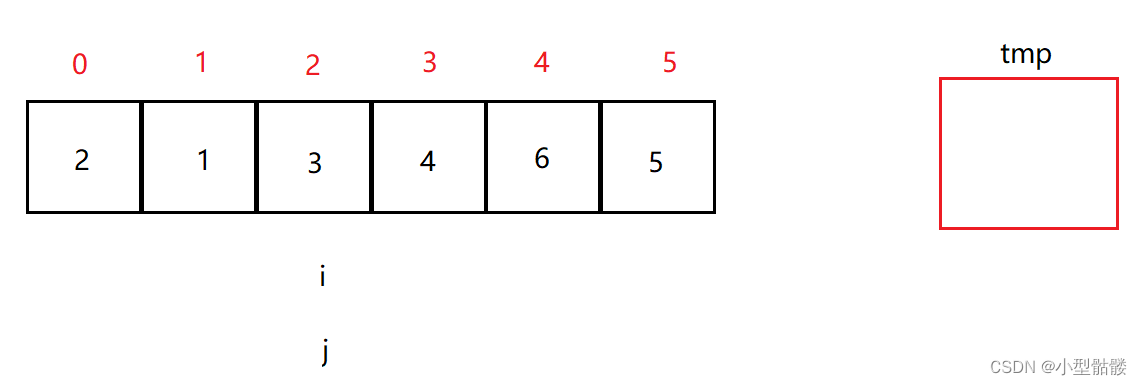
        当 i 和 j 相遇时，再把 tmp 里的值放进 i 和 j 相遇的那个坑里，这样就找到了基准值的下标了，此时的基准值3的位置是有序正确的，那么剩下的无序区间就变成了下标0 ~ 1，下标 3 ~ 5。之后再对剩下的两个无序区间进行以上的步骤：找基准值，找基准值的下标，再分成两个无序区间。无序区间的范围不断被缩小，直到区间长度小于等于1时，就说明该区间已经是有序得了，排序完成。

        代码实现：

// 快速排序（简单版）
    public static void quickSort2(int[] array){
        // 将这个区间进行快排
        quick2(array,0,array.length-1);
    }
 
// 对array数组的left到right区间进行排序
    private static void quick2(int[] array, int left, int right) {
        // 若left >= right 则说明这个区间不要快排，已经有序了
        if (left >= right){
            return;
        }
        // 获取基准值的下标
        int p = partition(array,left,right);
        // 对基准值左边的数组区间进行快排
        quick2(array,left,p-1);
        // 对基准值右边的数组区间进行快排
        quick2(array,p+1,right);
    }
 
 
    //partition函数用来找到数组中的“基准”【挖坑法】
    public static int partition(int[] array,int i,int j){
        int tmp = array[i]; //创建tmp作为中间值
        //开始循环，i从开头开始，j从结尾开始，当二者相遇时结束循环
        while (i < j){
            //将小于tmp的j值放到i处，若没有j前移
            while (i < j && array[j] >= tmp){
                j--;
            }
            array[i] = array[j];
            //再将大于tmp的值放到j处，若没有i后移
            while (i < j && array[i] <= tmp){
                i++;
            }
            array[j] = array[i];
        }
        //当二者相遇时，此时的值为“基准”
        array[i] = tmp;
        //返回“基准”值所在的下标
        return i;
    }

        时间复杂度：O(n * logn)；空间复杂度：O(logn)；稳定性：不稳定！

        当然，快速排序不止这么简单，我在选择基准值时是直接无脑选最左边的值，实际上基准值的选择还可以是随机选取或者几数取中法；另外，当待排序区间小于一个阈值时，使用直接插入排序会更加节省时间。 

七、归并排序

        排序思想：

        归并排序是分治法思想的一个非常经典的应用，主要采用的实现方法就是将两个有序数组进行合并，使其成为一个新的有序数组。

        当我拿到一个新的无序数组，我将这个无序数组从中间开始分为两个部分，这样我就得到了两个小的无序数组，再继续将其分解，又得到了四个小的无序数组，直到这些小的无序数组长度为1，即数组里只有一个元素的时候，我们就把它视为一个有序数组，然后和刚刚分解分开的另一个长度为1的有序数组进行合并，将这两个长度为1的数组合并为长度为2的有序数组，一直向上逆推，这样就可以把原来的无序数组排好序，变成有序数组了！

        例如以下数组，对其进行分解：

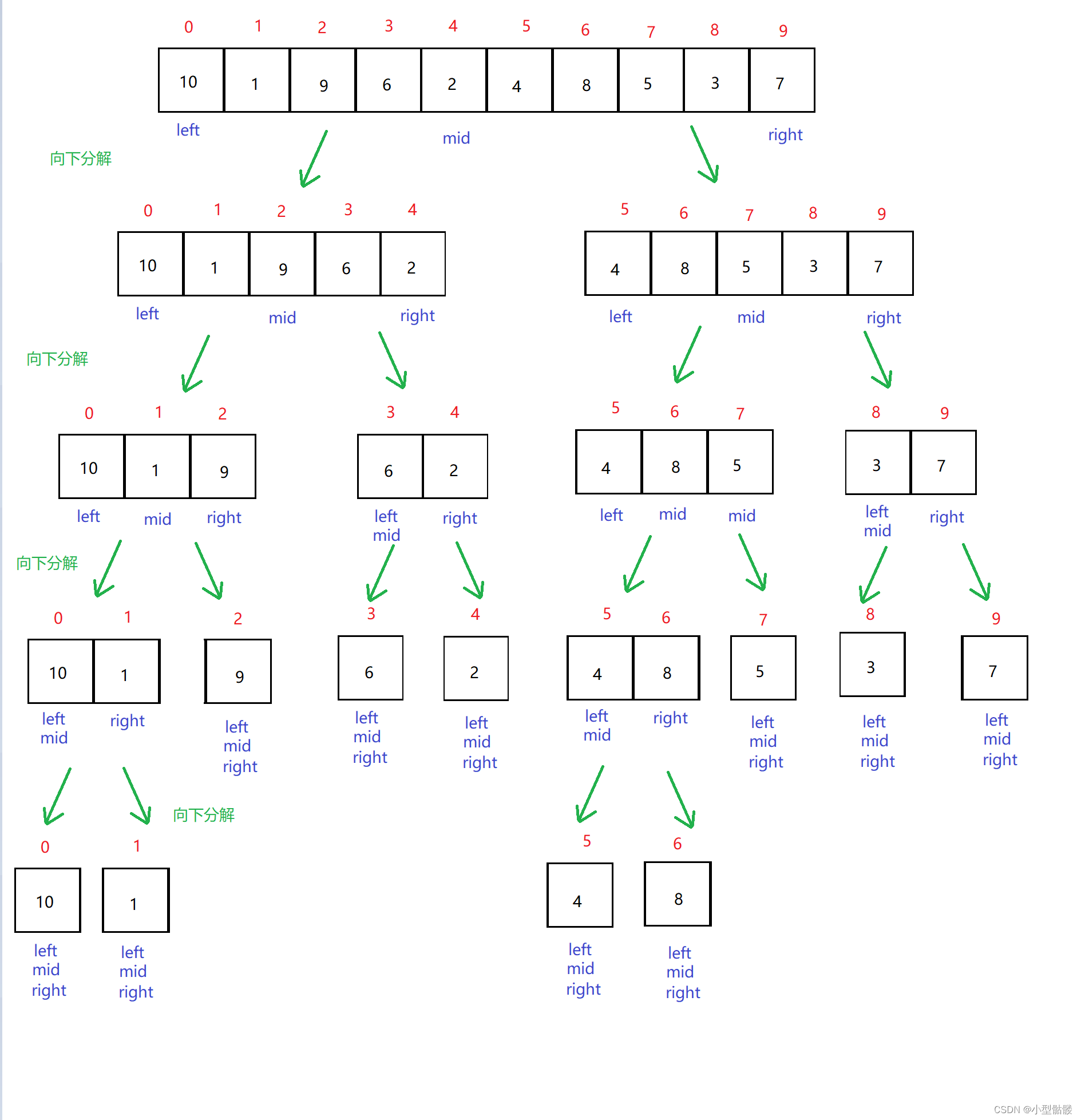
        分解完成之后，会变成一个个的小的有序数组，再对它们一个个向上合并：

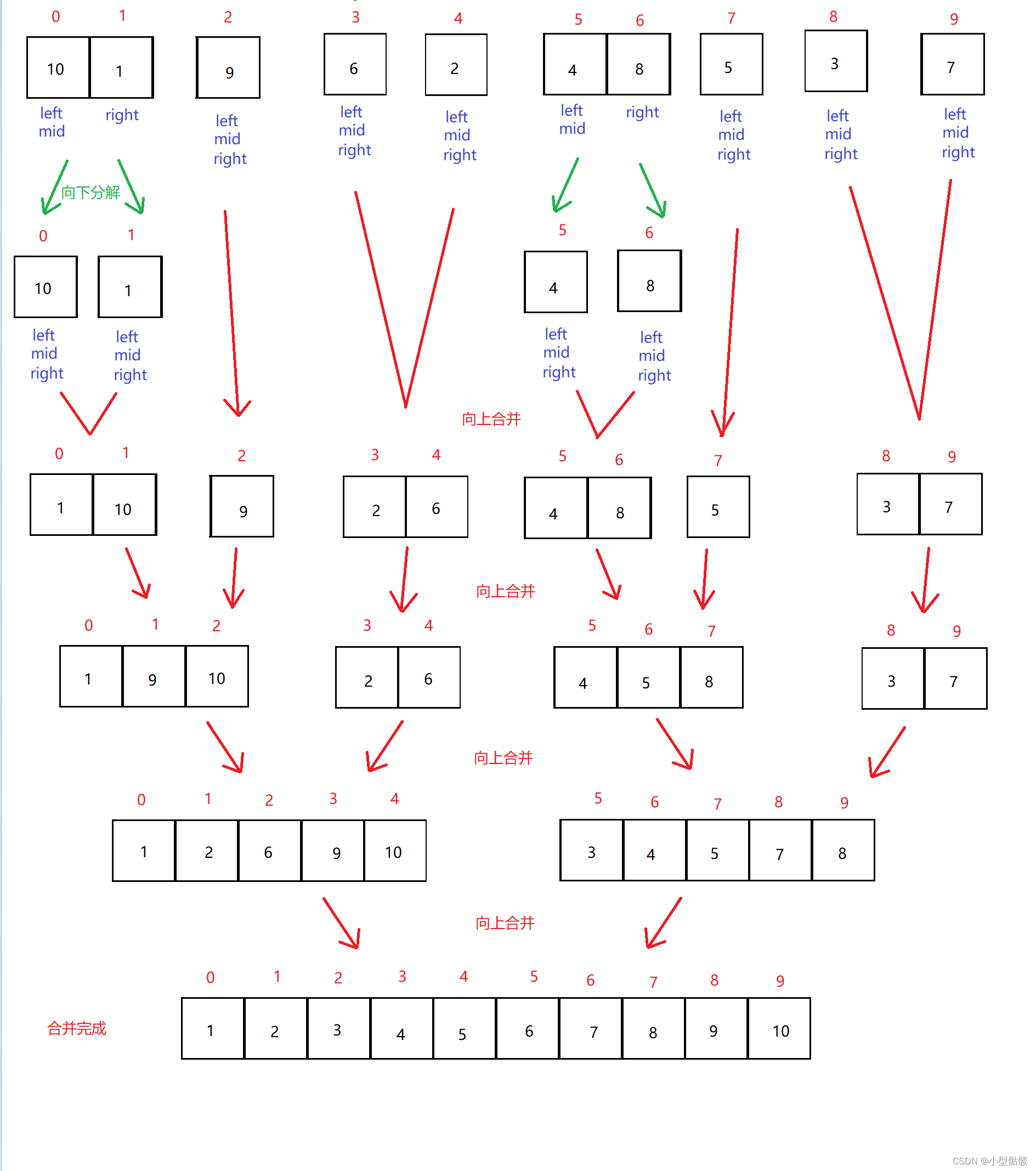
        最后就会合并成一个有序的数组，即归并排序。

        代码实现：

    // 归并排序
    public static void mergeSort(int[] array){
        // 对整个数组进行分解
        separate(array,0,array.length-1);
    }
 
    // 分解函数
    private static void separate(int[] array, int left, int right) {
        // 当left和right相遇或者大于时，不需要分解
        if (left >= right){
            return;
        }
        // 获取中间值
        int mid = (left + right) / 2;
        // 分解左半部分
        separate(array,left,mid);
        // 分解右半部分
        separate(array,mid+1,right);
        // 分解完毕后开始合并
        merge(array,left,mid,right);
    }
 
    // 合并函数
    private static void merge(int[] array, int left, int mid, int right) {
        // 创建tmp数组用来保存有序的新数组，tmp数组的范围是从left到right
        int[] tmp = new int[right - left + 1];
        // 设置两个区间的起始点
        int s1 = left,s2 = mid+1;
        // i来定义tmp数组的下标
        int i = 0;
        // 当s1走完或者s2走完时结束循环
        while (s1 <= mid && s2 <= right){
            // 判断s1和s2的大小，将较小的一个存进tmp数组内，之后往后移动一位
            if (array[s1] <= array[s2]){
                tmp[i++] = array[s1++];
            }else {
                tmp[i++] = array[s2++];
            }
        }
        // 判断s1和s2有没有走完它们的数组，若没走完继续将剩下的存进tmp
        while (s1 <= mid){
            tmp[i++] = array[s1++];
        }
        while (s2 <= right){
            tmp[i++] = array[s2++];
        }
        // 最后将有序数组tmp里的值再转存进array，使得array数组从left到right是有序的
        for (int j = 0; j < tmp.length; j++) {
            array[j + left] = tmp[j];
        }
    }

        时间复杂度：O(n * logn)；空间复杂度：O(n)；稳定性：稳定！