前缀和与树状数组（数据结构基础篇）

系列文章导引

• 系列文章导引

开源项目

本系列所有文章都将会收录到GitHub中统一收藏与管理，欢迎ISSUE和Star。

GitHub传送门：Kiner算法算题记

前言

在我们以往的文章中，经常会出现使用前缀和求取区间和的场景。但是，很多同学对于前缀和的概念和一些优缺点并不清楚，因此，这边发个单章单独聊一下前缀和与树状数组。

前缀和数组

初始化

时间复杂度为：O(n)，直接顺序遍历整个原数组累加即可

查询区间和

时间复杂度：O(1),由于初始化时已经将前n个元素的总和存储到了数组的第n位中，因此，我们想要求取第i位到第j位的区间和：s[j] - s[i]即可。

单点修改

时间复杂度：O(n),由于我们前缀和数组中的每一个元素都与之前的元素强相关，因此，只要任意元素改动都会影响到后面的所有元素的结果。由此可见，前缀和数组在处理元素组可能经常发生变化的场景时，效率是比较低的。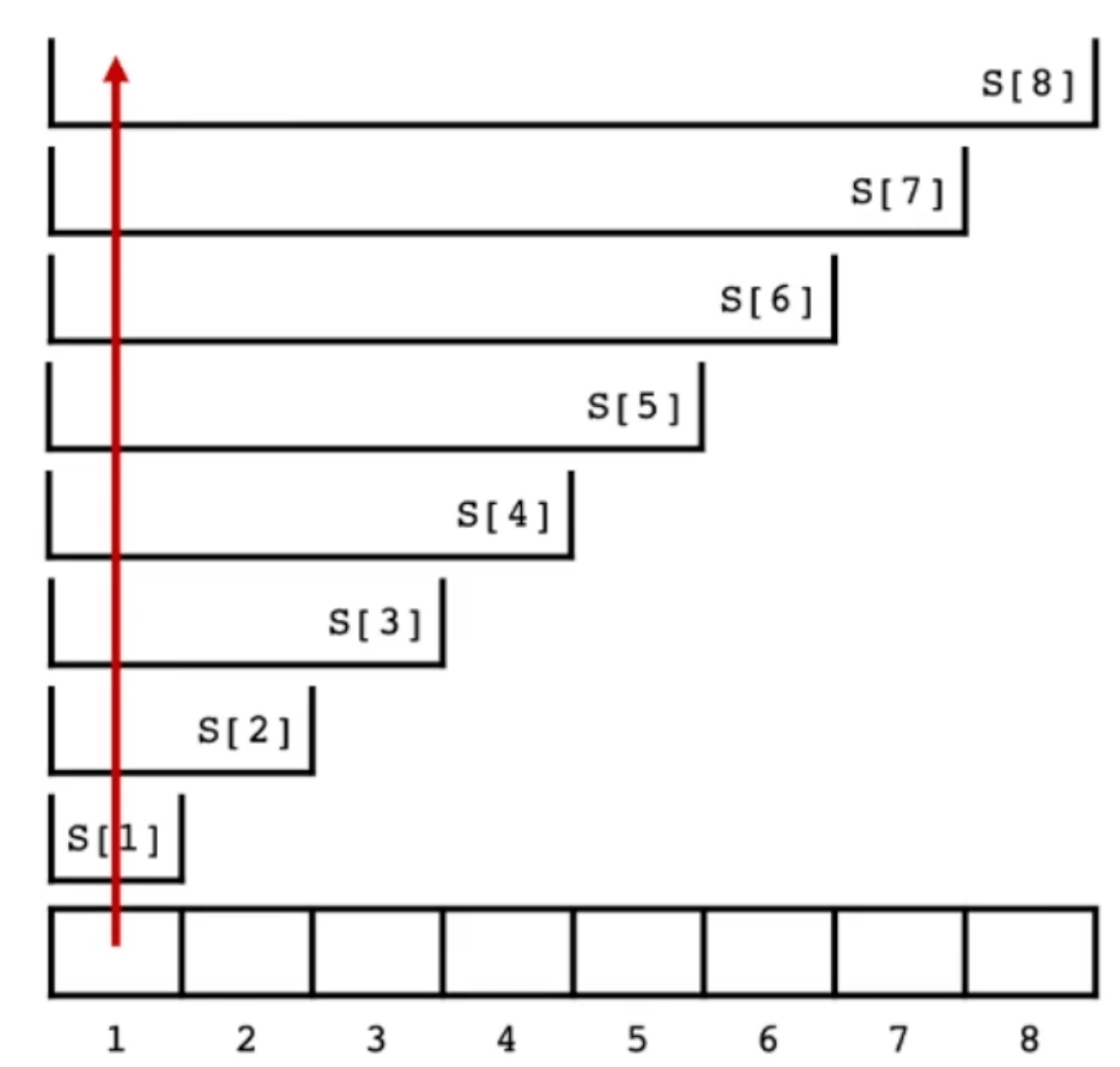

上图代表的是，如果我们修改了数组的第一项，那么我们数组之后的每一项都要跟着改

优化

弱化每个元素与前面元素强相关的关系，虽然会牺牲掉一定的查询区间和的速度，但同时能够提升单点修改的速度。

那么，我们具体要如何优化呢？首先，我们来接触一个概念：

lowbit

这是一个函数，这个函数的作用就是传入一个数字，返回这个数字二进制表示中最后一个1的位权。如：

lowbit(1) = 1;// 1的四位二进制表示为：0001，最后一个1代表的数字就是1
lowbit(2) = 2;// 2的四位二进制表示为：0010，最后一个1代表的数字就是2
lowbit(3) = 1;// 3的四位二进制表示为：0011，最后一个1代表的数字就是1
lowbit(4) = 4;// 4的四位二进制表示为：0100，最后一个1代表的数字就是4
lowbit(5) = 1;// 5的四位二进制表示为：0101，最后一个1代表的数字就是1
lowbit(6) = 2;// 6的四位二进制表示为：0110，最后一个1代表的数字就是2
lowbit(7) = 1;// 7的四位二进制表示为：0111，最后一个1代表的数字就是1
lowbit(8) = 8;// 8的四位二进制表示为：1000，最后一个1代表的数字就是8
lowbit(9) = 1;// 9的四位二进制表示为：1001，最后一个1代表的数字就是1
lowbit(10) = 2;// 10的四位二进制表示为：1010，最后一个1代表的数字就是2
lowbit(11) = 1;// 11的四位二进制表示为：1011，最后一个1代表的数字就是1
lowbit(12) = 4;// 12的四位二进制表示为：1100，最后一个1代表的数字就是4
lowbit(13) = 1;// 13的四位二进制表示为：1101，最后一个1代表的数字就是1
lowbit(14) = 2;// 14的四位二进制表示为：1110，最后一个1代表的数字就是2
lowbit(15) = 1;// 15的四位二进制表示为：1111，最后一个1代表的数字就是1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

从上面的示例中，大家应该都明白lowbit的作用了，在js当中，我们可以用以下方式实现lowbit函数：

function lowbit(num: number): number {
  return num & (-num);
}
1
2
3

假设C(i)代表前lowbit(i)项元素之和，如：

C[10] = a[10] + a[9]; // 由于lowbit(10) = 2,因此C[10]代表a[10]与a[9]的和
C[12] = a[12] + a[11] + a[10] + a[9];// 由于lowbit(12) = 4,因此C[12]代表a[12]、a[11]、a[10]与a[9]的和
1
2

相同的情况，如果原数组的第一位发生改变，我们需要改变的只有C[1]、C[2]、C[4]、C[8]，相比起传统前缀和数组，无疑需要修改的元素数量减少了。

树状数组

上述使用lowbit优化后的数组，就是树状数组，那么，我们的树状数组要如何查询前缀和呢？

查询前缀和

S[i] = S[i - lowbit(i)] + C[i]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A0NFjSXW-1659257824530)(https://ydschool-video.nosdn.127.net/1637756641072image-20211124202357546.png)]

例如，上图所示，如果我们想要求前7项的前缀和S[7] = S[7 - lowbit(7)] + C[7] = S[6] + C[7] = S[6 - lowbit(6)] + C[6] + C[7] = S[4] + C[6] + C[7] = C[4] + C[6] + C[7]

使用这个公式统计前缀和，时间复杂度是：log(n)。

单点修改操作

假如说我们要将原数组第5个元素在原来的基础上加上10，那么，都有哪些元素会相应发生变化呢？C[5]肯定会发生改变的，C[6]和C[8]也会因为C[5]改变而改变，因此，改变的元素有：C[5]、C[6]、C[8]。

那么，我们要如何确定C[6]和C[8]的值呢？大家先来思考一个问题：“之所以C[5]改变之后，C[6]和C[8]也会发生改变，是不是因为C[6]和C[8]包含的范围都包括了C[5],并且最少都比C[5]大1倍”。思考清楚这个事情之后，我们再来看一个公式：A[i] = C[i + lowbit(i)]。这个公式中的A[i]就是代表C[i]头顶上的元素，由于i + lowbit(i)的结果确定的范围至少是i确定范围的两倍，因此，刚好符合我们上面的推论。举个例子：

# C[i]
10000100
# C[i + lowbit(i)]
i:         10000100
lowbit(i): 00000100
=>         10001000
# 由于i+lowbit(i)肯定会导致原来的i进位，一旦进位，那么表示的范围至少都是原先的1倍
# 因此，我们可以通过下面公式求取头顶上的那个元素
A[i] = C[i + lowbit(i)]

# 如上图如果修改原数组的第五个元素 A[5]，我们如何通过公式确定需要修改树状数组中的那些元素呢
A[5] = C[5] + A[5 + lowbit(5)] = C[5] + A[6] = C[5] + C[6] + A[6 + lowbit(6)] = C[5] + C[6] + A[8] = C[5] + C[6] + C[8]
1
2
3
4
5
6
7
8
9
10
11
12

树状数组求解前缀和及单点修改代码演示

class FenwickTree {
    // 用于计算lowbit值
    static lowbit(x) {
        return x & -x;
    }
    // 树状数组
    private c: number[];
    // 数组的下标上线，一般是原数组长度加1
    private size: number;
    constructor(size: number) {
        this.size = size;
        this.c = new Array(size);
        this.c.fill(0);
    }
    /**
     * 往原始数组的第i位增加元素x
     * @param i 
     * @param x 
     */
    public add(i: number, x: number): void {
        while(i <= this.size) {
            this.c[i] += x;
            i += FenwickTree.lowbit(i);
        }
    }
    /**
     * 查询原数组前i项和
     * @param i 
     * @returns 
     */
    public query(i: number): number {
        let sum = 0;
        // S[i] = S[i - lowbit(i)] + C[i]
        while(i) {
            sum += this.c[i];
            i -= FenwickTree.lowbit(i);
        }
        return sum;
    }
    /**
     * 根据索引查找原始数组每一项的值
     * @param idx 
     * @returns 
     */
    public at(idx: number): number {
        return this.query(idx) - this.query(idx - 1);
    }
    /**
     * 将元素组第 idx 位的值改成 val
     * @param idx 
     * @param val 
     */
    public update(idx: number, val: number): void {
        console.log(`将第${idx}位的值改成: ${val}`)
        this.add(idx, val - this.at(idx));
    }
    public output(): void {
        let line1 = '';
        let line2 = '';
        let line3 = '';
        let line4 = '';
        let line5 = '';
        this.c.forEach((item, idx) => {
            if(idx === 0) return;
            line1+=String(idx).padStart(6, ' ');
            line2+=String("=").padStart(6, '=');
            line3+=String(item).padStart(6, ' ');
            line4+=String("=").padStart(6, '=');
            line5+=String(this.at(idx)).padStart(6, ' ');
        });
        // 编号
        console.log(line1);
        console.log(line2);
        // 树状数组值，当前所有元素都为1时，树状数组中第i位的值实际上就是lowbit(i)
        console.log(line3);
        console.log(line4);
        // 原数组的值
        console.log(line5+"\n\n");
    }
}

const source = [1,1,1,1,1,1,1,1,1,1];
const fenwickTree = new FenwickTree(source.length+1);
source.forEach((item, idx) => fenwickTree.add(idx+1, item));
fenwickTree.output();

//      1     2     3     4     5     6     7     8     9    10
// ============================================================
//      1     2     1     4     1     2     1     8     1     2
// ============================================================
//      1     1     1     1     1     1     1     1     1     1


fenwickTree.update(5, 10);
fenwickTree.output();
fenwickTree.update(3, 6);
fenwickTree.output();
fenwickTree.update(4, 7);
fenwickTree.output();
fenwickTree.update(2, 9);
fenwickTree.output();

// 将第5位的值改成: 10
//      1     2     3     4     5     6     7     8     9    10
// ============================================================
//      1     2     1     4    10    11     1    17     1     2
// ============================================================
//      1     1     1     1    10     1     1     1     1     1


// 将第3位的值改成: 6
//      1     2     3     4     5     6     7     8     9    10
// ============================================================
//      1     2     6     9    10    11     1    22     1     2
// ============================================================
//      1     1     6     1    10     1     1     1     1     1


// 将第4位的值改成: 7
//      1     2     3     4     5     6     7     8     9    10
// ============================================================
//      1     2     6    15    10    11     1    28     1     2
// ============================================================
//      1     1     6     7    10     1     1     1     1     1


// 将第2位的值改成: 9
//      1     2     3     4     5     6     7     8     9    10
// ============================================================
//      1    10     6    23    10    11     1    36     1     2
// ============================================================
//      1     9     6     7    10     1     1     1     1     1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132

扩展知识

差分数组

顾名思义，就是原数组相邻两位相减的差作为数组的每一个元素，举个例子：

# 原数组
1    2    3    4    5

# 前缀和数组（前缀和数组的第0位为特殊位，固定为0，实际使用时不会使用到，因此不做考虑）
S = 1    3    6    10   15
# 原数组
A = 1    2    3    4    5
# 差分数组，将数组的每一位为当前位与前一位相减的差值
X = 1    1    1    1    1
1
2
3
4
5
6
7
8
9

从上面的前缀和数组、原数组、差分数组的对比，我们可以发现前缀和数组是的每一位是当前位与上一位相加之和，而差分数组则是当前位与上一位相减之差，而且我们可以发现，如果只看S和A,那么S是A的前缀和数组、A是S的差分数组。如果只看A和X也是一样，A是X的前缀和数组，X是A的差分数组，因此，我们可以得出，实际上，前缀和数组和差分数组互为逆运算的结论。

接下来我们再来看一下，如果要在元素组的第i位到第j位都加上m，那么，在差分数组上有什么特性呢？

# 假如我们现在要在原数组A的第1位~第3位都加上2，即上述的i=1,j=3,m=2
# 原数组
A = 1    2+2    3+2    4+2    5
# 查分数组
X = 1    1+2    1      1    1+2

1
2
3
4
5
6

由上面的规律，我们不难看出，如果在原数组的第i位到第j位都加上m，那么在差分数组中的表现为在第i位和第j+1位加上m(i和j+1均小于数组长度)，即我们可以得出以下结论：

A[i, j, m] = X[i, j+1, m],其中A[i, j, m]代表原数组的第i位到第j位的数字均加上m的结果，而X[i, j+1, m]则代表在差分数组中，只有第i位和第j+1位需要加上m其他位不变。