1. 实验目的

理解逻辑回归模型，掌握逻辑回归模型的参数估计算法。

2. 实验要求

实现两种损失函数的参数估计（1.无惩罚项；2.加入对参数的惩罚），可以采用梯度下降、共轭梯度或者牛顿法等。

验证：

• 可以手工生成两个分别类别数据（可以用高斯分布），验证你的算法。考察类条件分布不满足朴素贝叶斯假设，会得到什么样的结果。
• 逻辑回归有广泛的用处，例如广告预测。可以到 UCI 网站上，找一实际数据加以测试。

3. 实验内容

3.1 算法原理

我们分类器做分类问题的实质，就是预测一个已知样本的位置标签，即 P(Y=1|x < x1, … , xn)。按照朴素贝叶斯的方法，可以用贝叶斯概率公式，将其转化为类条件概率（似然）和类概率的乘积。这次实验，是直接求该概率。

经过推导我们可以得到：

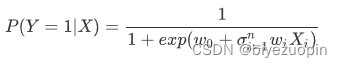
定义 sigmoid 函数为：

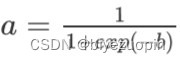
计算损失函数为：

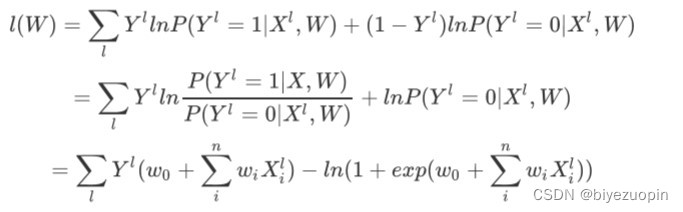
用梯度下降法求得 W = argmaxwl(w)，注意要用梯度下降的话，一般要把这里的 l(w)转化为相反数，-l(w)作为损失函数，求其最小值。

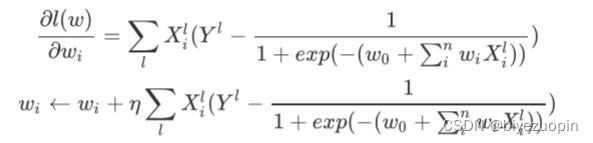
而我们加上正则项的梯度下降为

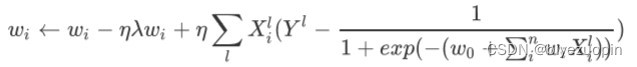
3.2 算法的实现

首先是生成数据，如果要生成类条件分布满足朴素贝叶斯假设的数据，那么就对每一个类别的每一个维度都用一个独立的高斯分布生成。如果要生成类条件分布不满足朴素贝叶斯假设的数据，那么 就对每一个类别的两个维度用一个二维高斯分布生成。需要注意的是，由于高斯分布具有的特性， 多维高斯分布不相关可以推出独立性，因此，可以用二维高斯分布生成数据，如果是满足朴素贝叶斯假设的，那么协方差矩阵的非对角线元素均为 0，如果是不满足朴素贝叶斯假设的，那么协方差矩阵的非对角线元素不为 0（协方差矩阵应该是对称阵）。

计算极大似然估计:

梯度下降算法：

在做 UCI 上的数据时，选取了皮肤 Skin_NonSkin.txt 数据。由于该数据量太大，这里只选取了其中一部分。

读取数据时，用 numpy 切片提取数据信息，用 50 作为步长，提取部分数据用做实验。还要对样本点进行空间平移，否则在计算 MCLE 时可能会溢出，因为计算 MCLE 时，要用参数与样本做矩阵乘法，而且还要作为的指数计算，可能会溢出。

4. 实验结果

自己生成数据

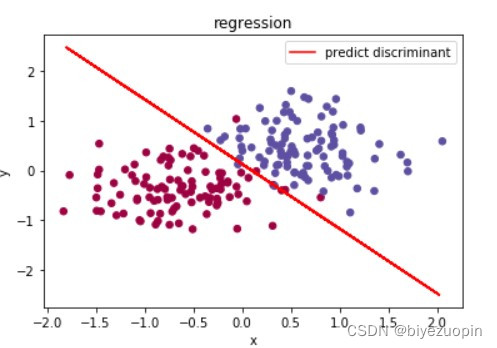
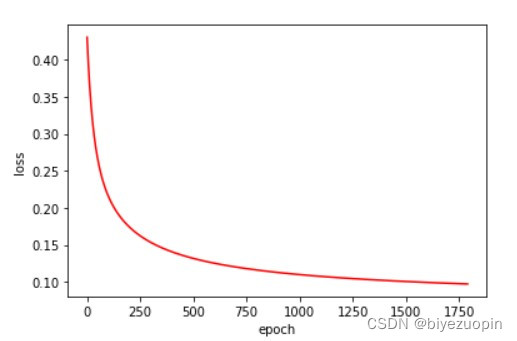
类条件概率满足朴素贝叶斯假设，正则项 λ=0，size=200

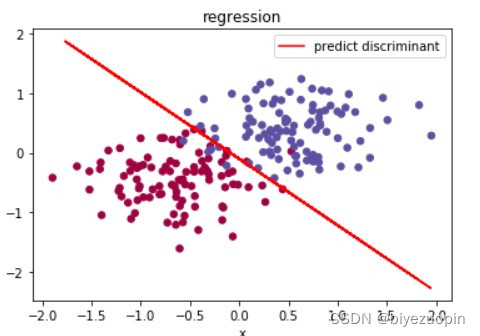
类条件概率不满足朴素贝叶斯假设，正则项 λ=0，size=200

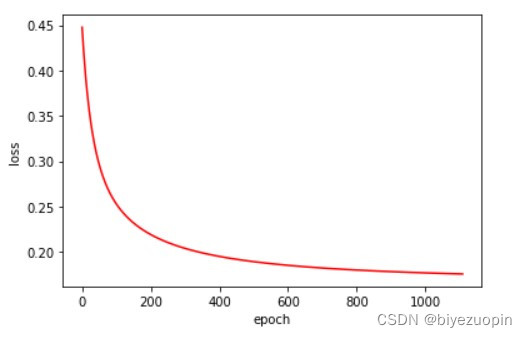
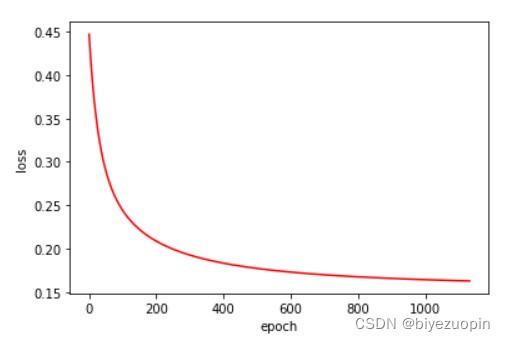
类条件分布满足朴素贝叶斯假设，正则项 λ=0.001，size=200

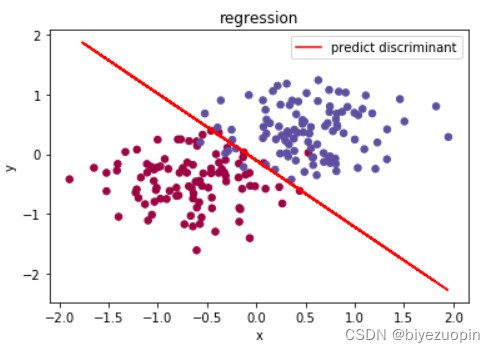
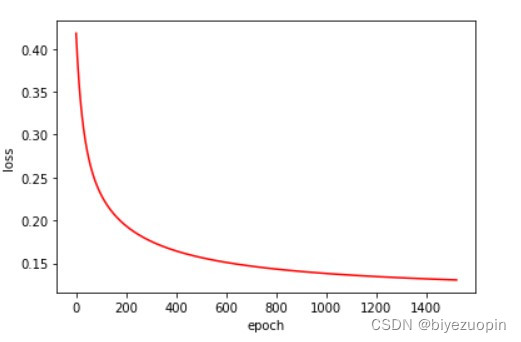
类条件概率不满足朴素贝叶斯假设，正则项 λ=0.001，size=200

UCI 皮肤颜色数据集

正则项 λ=0

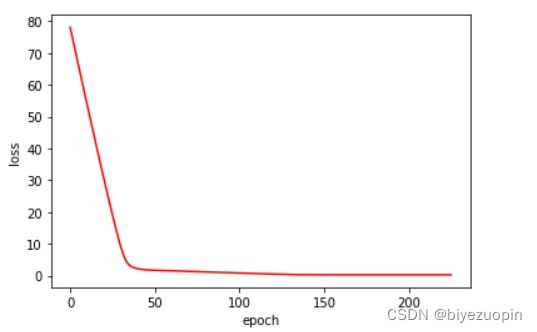
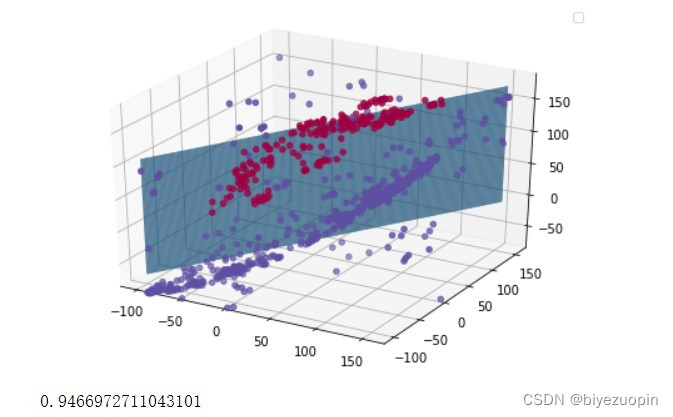
正则项 λ=0.01

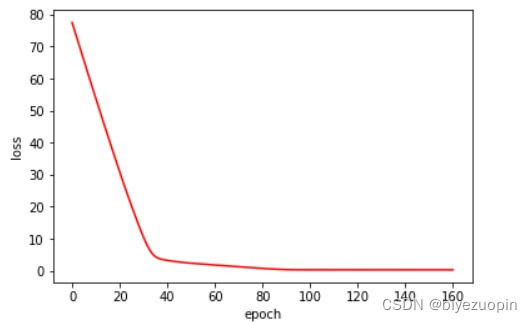
UCI banknote 数据集

正则项 λ=0

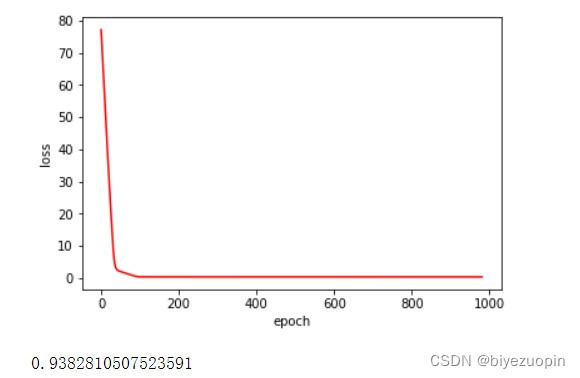
正则项 λ=0.01

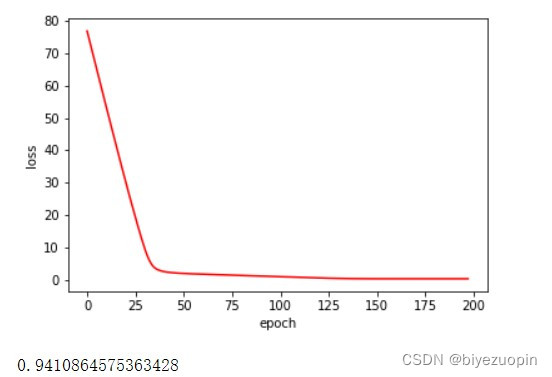
实验发现，UCI 的数据的 20% 测试集的准确率基本稳定在 93%-94%。 正则项在数据量较大时，对结果的影响不大，在数据量较小时， 应可以有效解决过拟合问题。 类条件分布在满足朴素贝叶斯假设时的分类表现，要比不满足假设时略好。 logistics 回归可以很好地解决简单的线性分类问题，而且收敛速度较快。
量较大时，对结果的影响不大，在数据量较小时， 应可以有效解决过拟合问题。 类条件分布在满足朴素贝叶斯假设时的分类表现，要比不满足假设时略好。 logistics 回归可以很好地解决简单的线性分类问题，而且收敛速度较快。