• 算法提升①

    目录

    一、求递归的时间复杂度

    1、对递归的认识

    ​编辑2、master公式的使用

    二、归并排序

    归并排序的扩展

    小和问题

    逆序对问题

    三、荷兰国旗问题

    1、问题1

    2、问题2（荷兰国旗问题）

    3、利用荷兰国旗问题优化快排

    优化1

    优化2

    四、堆排序

    1、大根堆和小根堆

    2、基本思想

    一、求递归的时间复杂度

    1、对递归的认识

    递归其实就是一个压栈操作，将母问题规模不断分解，有点类似于二叉树后序遍历。

    例如用递归方法找一个数组中的最大值。

    求[3, 2, 5, 6, 7, 4]数组中的最大值

    我需要找到数组0 - 5号位中的最大值，我需要先找到0 - 2号位和3 - 5号位的最大值

    找0 - 2号位的最大值，我需要先找0 -1号位的最大值和1 - 2号位的最大值...

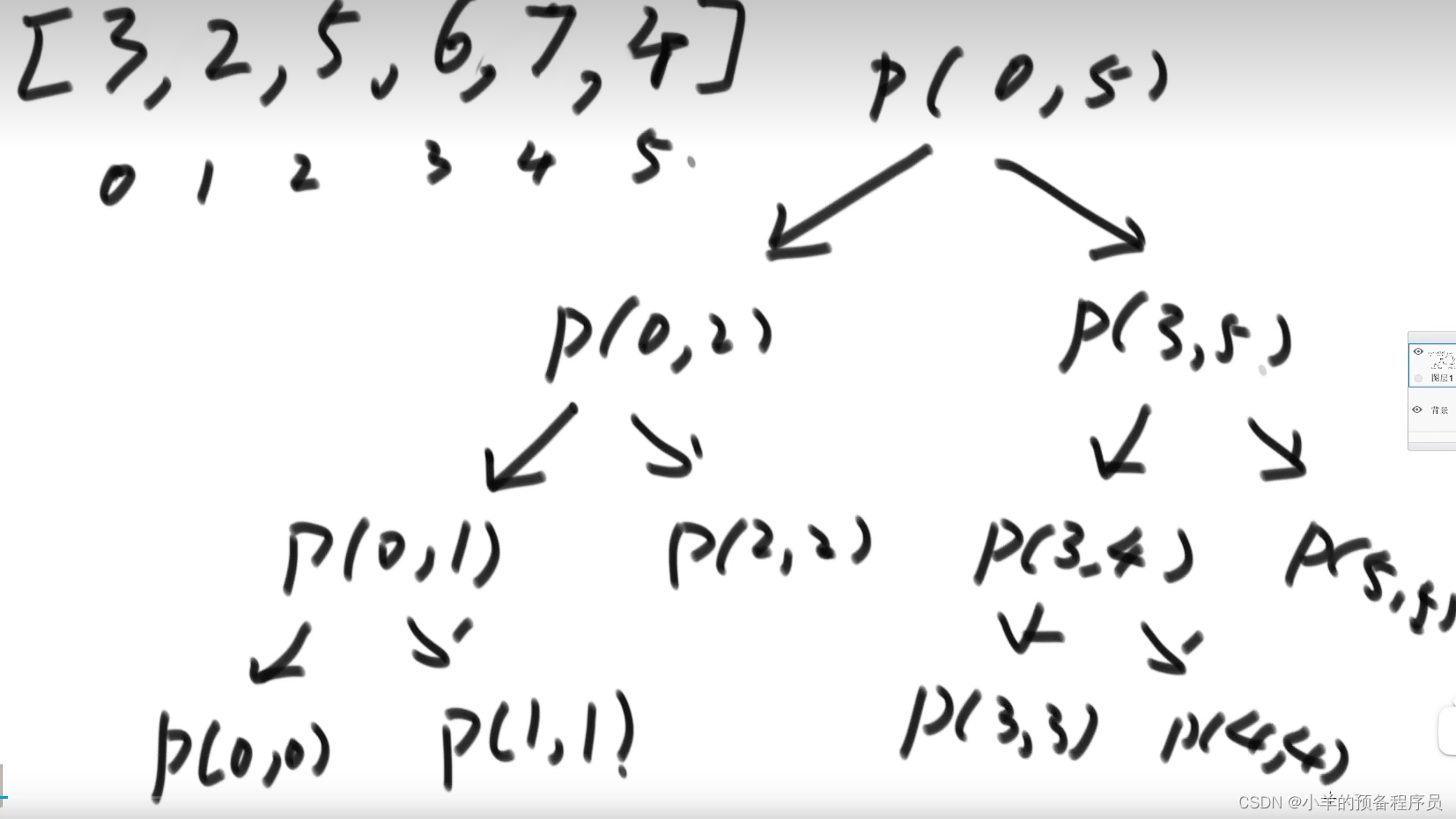    2、master公式的使用

    能使用master公式的前提：子问题的递归规模是母问题的O(N/b)，并且能拆分成多个同样规模的子问题加上一个规模O（N^b）的问题。

    当a，b，d三个参数确定，那么母问题递归的时间复杂度就已经确定了 

    例如用递归方法找一个数组中的最大值。

    1. int getMax(int arr[], int length)
    2. {
    3.     return process(arr, 0, length - 1);
    4. }
    5.  
    6. int process(int arr[], int L, int R)
    7. {
    8.     //范围只有一个数，直接返回
    9.     if(L == R)
    10.     {
    11.         return arr[L];
    12.     }
    13.     int mid = L + ((R - L)>>1); //中点，可以防止int溢出
    14.     int leftMax = process(arr, L, mid);
    15.     int rightMax = process(mid + 1, R);
    16.     return leftMax > rightMax ? leftMax : rightMax;
    17. }

    上面实现的递归算法子问题是两次规模是母问题一半的递归O(N/2)（寻找中点左边范围的最大值和寻找重点右边范围的最大值），再加上一次左边的最大值和右边的最大值比较得到最大值的一个O(N^0)的问题

    满足master公式，其中a = 2，b = 2，d = 0；

    并且loga b > d，所以该递归方法的时间复杂度为O(N^loga b)，O(N)。

    二、归并排序

    （1）整体就是一个简单递归，左边排好序、右边排好序、让整体有序

    （2）让其整体有序的过程里用了外排序方法

    （3）利用master公式来求解时间复杂度

    （4）归并排序的实质

    时间复杂度O(N*logN)，额外空间复杂度O(N)

    1. //归并排序
    2. //1、给中点左边和右边排序
    3. //2、归并
    4.  
    5. void merge(int arr[], int L, int Mid, int R)
    6. {	
    7. 	//arr1是临时数组
    8. 	int* arr1 = new int[R - L + 1];
    9. 	int i = 0;
    10. 	int p1 = L;
    11. 	int p2 = Mid + 1;
    12. 	//先排完一边
    13. 	while (p1 <= Mid && p2 <= R)
    14. 	{
    15. 		arr1[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
    16. 	}
    17. 	//剩下的直接放在临时数组
    18. 	while (p1 <= Mid)
    19. 	{
    20. 		arr1[i++] = arr[p1++];
    21. 	}
    22. 	while (p2 <= R)
    23. 	{
    24. 		arr1[i++] = arr[p2++];
    25. 	}
    26. 	//将有序数组拷贝回原数组
    27. 	for (i = 0; i < R - L + 1; i++)
    28. 	{
    29. 		arr[L + i] = arr1[i];
    30. 	}
    31. 	delete [] arr1;
    32. }
    33.  
    34. void process(int arr[], int L, int R)
    35. {
    36. 	if (L == R)
    37. 	{
    38. 		return;
    39. 	}
    40. 	int mid = L + ((R - L) >> 1);
    41. 	process(arr, L, mid);
    42. 	process(arr, mid + 1, R);
    43. 	merge(arr, L, mid, R);
    44. }
    45.  
    46. void merge_sort(int arr[], int length)
    47. {
    48. 	return process(arr, 0, length - 1);
    49. }
    50.  
    51. int main()
    52. {
    53. 	int arr[10] = { 5, 4, 6, 2, 1, 3, 7, 8, 9, 10 };
    54. 	merge_sort(arr, 10);
    55. 	for (int i = 0; i < 10; i++)
    56. 	{
    57. 		printf("%d ", arr[i]);
    58. 	}
    59. 	system("pause");
    60. 	return 0;
    61. }

    归并排序符合master公式，整个排序的时间复杂度为O(N*logN)

    思考：为什么冒泡排序和插入等算法时间复杂度为O(N^2)？他们差在哪里

    因为他们浪费大量的比较行为，冒牌排序等O(N^2)的算法在0 - N -1 范围的比较只确定了一个数的位置，而归并排序并没有浪费比较行为，归并的时候两个指针将信息通过空间传递下来了，变成了一个整体有序的部分，然后通过递归，整体有序的部分不断变成更大的整体有序的部分，所以归并排序算法做到了时间复杂度为O(N*logN)。

    归并排序的扩展

    小和问题和逆序对问题

    小和问题

    在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

    例子：[1，3，4，2，5]1左边比1小的数，没有；3左边比3小的数，1；4左边比4小的数，1、3；2左边比2小的数，1；5左边比5小的数，1、3、4、2；所以小和等于1+1+3+1+1+3+4+2=16

    暴力求解：每到数组一个位置，遍历比较前面的数字求和，时间复杂度为O(N^2)

    利用归并排序：小和问题不妨转化思路，找左边比当前数小，等价于找右边有多少个数比当前数大，例如上述例子1的右边有四个数比1大，就会产生4个1；3的右边有两个数比3大，就会产生2个3；4的右边有一个数比4大；就会产生1个4；2的右边有一个数比2大，就会产生一个2；5的右边没有数比他大，就不会产生5；所以小和等于4*1+2*3+1*4+1*2=16；这个过程在归并排序的时候可以直接使用，具体代码如下：

    1. int merge(int arr[], int l, int mid, int r)
    2. {
    3. 	//与归并排序的不同是求小和当指针指向的元素相等的时候，先拷贝右边的元素
    4. 	int* help = new int[r - l + 1];
    5. 	int i = 0;
    6. 	int p1 = l;
    7. 	int p2 = mid + 1;
    8. 	int res = 0;
    9. 	while(p1 <= mid && p2 <= r)
    10. 	{
    11. 		res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
    12. 		help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
    13. 	}
    14. 	while (p1 <= mid)
    15. 	{
    16. 		help[i++] = arr[p1++];
    17. 	}
    18. 	while (p2 <= r)
    19. 	{
    20. 		help[i++] = arr[p2++];
    21. 	}
    22. 	//将排好序的数组拷贝回原数组
    23. 	for (i = 0; i < r - l + 1; i++)
    24. 	{
    25. 		arr[l + i] = help[i];
    26. 	}
    27. 	delete[] help;
    28. 	return res;
    29. }
    30.  
    31. //归并的过程既要排序也要求小和
    32. int process(int arr[], int l, int r)
    33. {
    34. 	if (l == r)
    35. 	{
    36. 		return 0;
    37. 	}
    38. 	//求中点，写成这个形式是防止整形溢出的情况
    39. 	int mid = l + ((r - l) >> 1);
    40. 	return 	process(arr, l, mid)
    41. 			+ process(arr, mid + 1, r)
    42. 			+ merge(arr, l, mid, r);
    43. }
    44.  
    45. int smallSum(int arr[], int length)
    46. {
    47. 	if (arr == NULL || length < 2)
    48. 	{
    49. 		return 0;
    50. 	}
    51. 	return process(arr, 0, length - 1);
    52. }
    53.  
    54. int main()
    55. {
    56. 	int arr[5] = { 1, 3, 4, 2, 5 };
    57. 	int res = smallSum(arr, 5);
    58. 	cout << "res = " << res << endl;
    59. 	system("pause");
    60. 	return 0;
    61. }

    逆序对问题

    在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请找到逆序对的数量

    1. class Solution {
    2. public:
    3.     int reversePairs(vector<int>& nums) {
    4.         //归并实现逆序对
    5.         if(nums.size() < 2)
    6.         {
    7.             return 0;
    8.         }
    9.         return mergeSort(nums, 0, nums.size() - 1);
    10.     }
    11. private:
    12.     int mergeSort(vector<int>& nums, int L, int R)
    13.     {
    14.         if(L == R)
    15.         {
    16.             return 0;
    17.         }
    18.         int mid = L + ((R - L)>>1);
    19.         return mergeSort(nums, L, mid)
    20.             + mergeSort(nums, mid + 1, R)
    21.             + merge(nums, L, mid, R);
    22.     }
    23.     int merge(vector<int>& nums, int L, int mid, int R)
    24.     {
    25.         //准备一个临时数组
    26.         int* help = new int[R - L + 1];
    27.         int i = 0;
    28.         int p1 = L;
    29.         int p2 = mid + 1;
    30.         int res = 0;
    31.         while(p1 <= mid && p2 <= R)
    32.         {
    33.             if(nums[p1] <= nums[p2])
    34.             {
    35.                 help[i++] = nums[p1++];
    36.             }
    37.             else
    38.             {
    39.                 help[i++] = nums[p2++];
    40.                 res += mid - p1 + 1;
    41.             }
    42.         }
    43.         while(p1 <= mid)
    44.         {
    45.             help[i++] = nums[p1++];
    46.         }
    47.         while(p2 <= R)
    48.         {
    49.             help[i++] = nums[p2++];
    50.         }
    51.         //将排序完的数组拷贝回原数组
    52.         for(int i = 0; i < R - L + 1; i++)
    53.         {
    54.             nums[L + i] = help[i];
    55.         }
    56.         delete[] help;
    57.         return res;
    58.     }
    59. };

    三、荷兰国旗问题

    1、问题1

    给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组

    的右边。要求额外空间复杂度0(1)，时间复杂度0(N)

    2、问题2（荷兰国旗问题）

    给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中

    间，大于num的数放在数组的右边。要求额外空间复杂度0(1)，时间复杂度0(N)

    3、利用荷兰国旗问题优化快排

    优化1

    快排基础版本和问题1类似，选择最后一个数作为基准，把数组划分为两个区域，一个大于区，一个小于区，最后将该数与大于区第一个交换，然后你所选取的该数就在整个数组中已经排好序了，最后利用递归分别对大于区和小于区进行排序，但是本质上一次排序只搞定了确定大于区和小于区和确定一个数的位置，利用荷兰国旗问题，可以搞定一堆等于该数据的数的位置，所以比普通快排速度更快更优，但是普通快排和优化后的快排的时间复杂度都是0(N^2)，因为如果数组是[1,2,3,4,5,6,7,8,9]，就会遇到最坏情况，因为划分值太偏了，所以可以继续优化

    优化2

    因为选取数据的问题，就有可能人为制造出最差情况，不妨随机选一个数，然后让你选取的数与数组最后一个数交换位置，然后利用优化1版本再去快排。这样出来的时间复杂度为O(N*logN)，为什么是O(N^2)呢，不妨假设你选取的数据在1/5,2/5,3/5...位置，这些数据出现的概率都是等概率时间，根据master公式可以分别计算出每一个位置的时间复杂度，然后通过概率时间相加对概率求数学期望求出时间复杂度为O(N*logN)，具体证明比较复杂，就不写上。直接看优化代码如下：

    四、堆排序

    堆的结构可以分为大根堆和小根堆，是一个完全二叉树，而堆排序是根据堆的这种数据结构设计的一种排序，下面先来看看什么是大根堆和小根堆

    1、大根堆和小根堆

    性质：每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆；每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。如下图

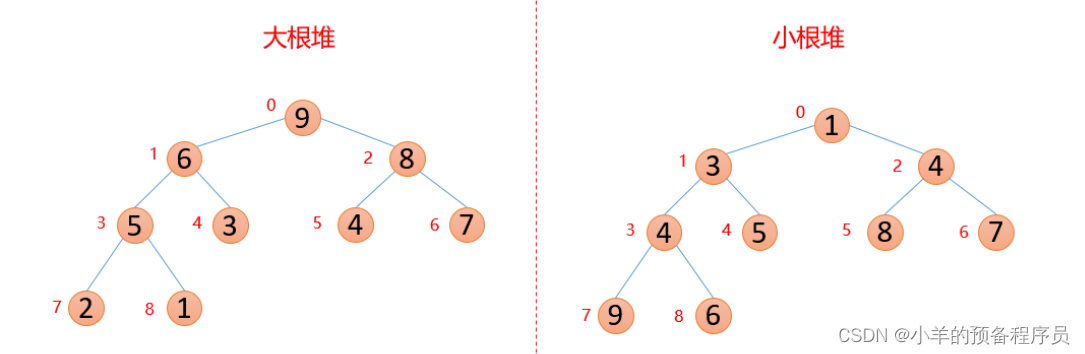
    还有一个基本概念：查找数组中某个数的父结点和左右孩子结点，比如已知索引为i的数，那么

    1.父结点索引：(i-1)/2（这里计算机中的除以2，省略掉小数）

    2.左孩子索引：2*i+1

    3.右孩子索引：2*i+2

    2、基本思想

    1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

    2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

    3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

    代码实现如下：

    1. void swap(int arr[], int pos1, int pos2)
    2. {
    3. 	int temp = arr[pos1];
    4. 	arr[pos1] = arr[pos2];
    5. 	arr[pos2] = temp;
    6. }
    7.  
    8. //某个数在index位置，能否往上移动
    9. void heapInsert(int arr[], int index)
    10. {
    11. 	while (arr[index] > arr[(index - 1) / 2])
    12. 	{
    13. 		swap(arr, index, (index - 1) / 2);
    14. 		index = (index - 1) / 2;
    15. 	}
    16. }
    17.  
    18. //某数在index位置，能否往下移动
    19. void heapify(int arr[], int index, int heapSize)
    20. {
    21. 	int left = index * 2 + 1;//左孩子下标
    22. 	while (left < heapSize)
    23. 	{
    24. 		//下方还有孩子的时候
    25.  
    26. 		//两个孩子中，谁的值大，把下标给largest
    27. 		int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
    28. 		//父和孩子之间，谁的值最大，把下标给largest
    29. 		largest = arr[largest] > arr[index] ? largest : index;
    30. 		if (largest == index)
    31. 		{
    32. 			break;
    33. 		}
    34. 		swap(arr, largest, index);
    35. 		index = largest;
    36. 		left = index * 2 + 1;
    37. 	}	
    38. }
    39.  
    40. void heapSort(int arr[], int length)
    41. {
    42. 	if (arr == NULL && length < 2)
    43. 	{
    44. 		return;
    45. 	}
    46. 	for (int i = 0; i < length; i++)
    47. 	{
    48. 		heapInsert(arr, i);//O(logN)
    49. 	}
    50. 	int heapSize = length;
    51. 	swap(arr, 0, --heapSize);
    52. 	while (heapSize > 0)
    53. 	{
    54. 		//O(N)
    55. 		heapify(arr, 0, heapSize);//O(logN)
    56. 		swap(arr, 0, --heapSize);//O(1)
    57. 	}
    58. }
    59.  
    60. int main()
    61. { 
    62. 	int arr[10] = { 1, 2, 4, 5, 7, 8, 3, 9, 10, 6 };
    63. 	heapSort(arr, 10);
    64. 	for (int i = 0; i < 10; i++)
    65. 	{
    66. 		printf("%d ", arr[i]);
    67. 	}
    68. 	system("pause");
    69. 	return 0;
    70. }

  • 相关阅读:
    【大话设计模式】策略模式
    微服务设计模式-架构真题（六十八）
    【Nuxt】03 Nuxt2 页面缓存、组件缓存、api缓存
    探索SPI：深入理解原理、源码与应用场景
    大语言模型（LLM）工作的3个步骤，一文带你搞清楚！
    矩阵分析与应用+张贤达
    网站收录量与索引量有什么区别？
    APS计划排产在卫浴行业的应用
    SpringBoot Starter缘起
    机器学习（四十五）：使用Flask构建机器学习web
  • 原文地址：https://blog.csdn.net/qq_51654808/article/details/126055410