补充：
《程序员的数学2概率统计》一书中1.3章节。
将概率问题比喻成了一个个平行世界的组合，使用希腊字母小写$\omega$表示具体每一个世界，使用希腊字母大写$\Omega$表示所有平行世界组成的大集合。
$\Omega$的子集A（如果不习惯这个词，可以理解为$\Omega$中的区域A）的面积将由$P(A)$表示。

期望值

简单来说，对于取值不确定的随机值，将其可能的平均值称为期望值，值的分散情况称为方差。

随机变量记为$X$，期望值记为$E[X]$。

假设有A、B、C三种情况，概率分别$\frac{1}{6}$，$\frac{1}{3}$，$\frac{1}{2}$，三种情况的概率之和为1（实际全部情况的概率之和为1），现在将ABC三种情况理解为一个正方形中的三个区域。不同的概率分别是各自的面积大小，而正方形整体的面积为1。
假设A区域的随机数=5，B区域的随机数=2，A区域的随机数=1，将每个区域出现的值作为高度绘图，就可以得到如下快状体。

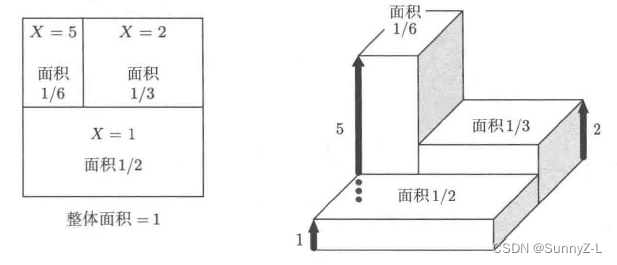
将上图右侧块状体的体积称为期望值，记为$E[X]$。则期望值的计算过程如下

$$E[X]=5\ast \frac{1}{6}+2\ast \frac{1}{3}+1\ast \frac{1}{2}=2$$

将期望值理解为所有平行世界的平均值。通过雪国的故事或许可以帮助读者理解这个概念。假设$\Omega$国有A、B、C三个省份，各省的面积分别为$\frac{1}{6}$，$\frac{1}{3}$，$\frac{1}{2}$，全国的总面积为1。某一天，$\Omega$国下雪了，A、B、C省的积雪分别是5m、3m、1m。现在想要计算全国的平均积雪情况。也就是说，如果将学铺满整个国家后积雪将有多深呢？答案是$E(X)$，则$E(X)$的计算如下

$$E[X]=\frac{5\ast \frac{1}{6}+2\ast \frac{1}{3}+1\ast \frac{1}{2}}{1}=2$$

方差和标准差

方差即“期望值离散程度”的期望值

假设随机变量$X$的期望值$E[X]=\mu$。习惯上，随机值$X$以大写字母表示，它的期望值$\mu$是一个定值，因此用小写字母表示。

由于$X$是个一个随机变量，因此即使它的期望值为$\mu$，也不表示它的值就一定等于$\mu$。为此，需要计算它的实际取值$x$与$\mu$的差距。
测量的方式有很多。$|x-\mu |$可能是最为直观的方法，但是在实际计算时，绝对值的存在会带来诸多不便。于是人们通常使用偏差的平方$(x-\mu {)}^2$而非绝对值来解决这个问题。

• 如果$X$的取值正巧为$\mu$，$(x-\mu {)}^2$=2
• 否则$(x-\mu {)}^2>0$
• 且$x$与$\mu$的偏差越大，$(x-\mu {)}^2$的值也越大，即数据也就越分散。

这些性质非常否和离散的程度。
不过，由于$X$是一个随机值，直接计算$(x-\mu {)}^2$得到的也将是一个随机值，而我们希望得到的是一种固定指标，因此需要进一步计算它的期望值$E[(x-\mu {)}^2]$，来消除随机性。用这种方式得到的“离散程度的期望值”称为方差(variance)，记为$V[X]$或$Var[X]$。

方差用于衡量随机变量的离散程度。$V[X]$的值越大，随机变量的值就越分散， 值越小，随机变量的值就越集中。但是对于$V[X]=25$和$V[X]=100$，是否能够想象其分散的程度呢？方差结果相差4倍，但是二者实际的分散程度是4倍吗？

通过方差的计算$(x-\mu {)}^2$可以得知，方差是平方后的结果，假设$X$表示的是长度，方差$V[X]$表示的是长度的平方，并不是长度，因此二者无法直接比较。

我们通常通过平方根运算将方差还原成长度。诸如此类的方差的平方根称为标准差(standard deviation)，通常记为$\sigma$或$s$。

---

《程序员的数学2概率统计》笔记