-
数据结构刷题——图论
一、【模板】拓扑排序
解法:
本题可分为两部分:
1.根据输入使用邻接表建图,并将每个顶点的入度记录下来;
2.采用类似于BFS(广搜)的思想,依次遍历入度为0的顶点,并根据邻接表进行相应顶点入度的调整,最终判断是否可以得到拓扑排序并进行相应的输出。对于第一部分,可以使用每个元素为一个数组的vector容器模拟邻接表进行建图,vector[a]所对应的数组中存储着该顶点所指向的其他顶点。之后使用一个数组inDegree记录每个顶点的入度。
对于第二部分,可以使用一个队列,初始时将所有入度为0的顶点全部入队,之后采用BFS的思想,依次取出队头元素并存入结果数组中,然后在邻接表中遍历该队头元素所指向的其他顶点,将这些顶点的入度全部减一,若减一后某顶点的入度变为0,则将该顶点进行入队操作,重复此步骤直至队列为空为止。
【需要设置一个用于判断图中是否存在环(是否可以得到拓扑序列)的计数器,在弹出队头元素后要将计数器加一,最后队列为空后,若计数器的值与顶点数相同,则说明图不存在环,可以得到拓扑序列。】#include#include #include #define MAX 200001 using namespace std; int main() { int n, m; cin>>n>>m; vector<int> adjlist[MAX]; // 用于模拟邻接表的vector容器 int inDegree[MAX] = {0}; // 用于记录每个顶点入度的数组,初始值全部设置为0 int a, b; for(int i = 0; i < m; i++) { cin>>a>>b; adjlist[a].push_back(b); inDegree[b]++; } queue<int> que; for(int i = 1; i <= n; i++) { if(inDegree[i] == 0) // 将初始入度为0的顶点全部入队 { que.push(i); } } int cnt = 0; // 用于判断图中是否存在环的计数器 vector<int> res; // 用于存储结果序列的数组 while(!que.empty()) { int u = que.front(); que.pop(); res.push_back(u); // 存储结果用于输出 for(int i = 0; i < adjlist[u].size(); i++) // 遍历该顶点指向的其他顶点 { int v = adjlist[u][i]; inDegree[v]--; // 被指向的顶点的入度减一 if(inDegree[v] == 0) // 若顶点的入度减为0,则将其入队 { que.push(v); } } cnt++; } if(cnt == n) // 若计数器与顶点数相同则图无环,存在拓扑序列 { for(int i = 0; i < res.size(); i++) { cout<<res[i]; if(i != res.size() - 1) // 此处注意:本题最后一个数字后不能输出多余空格,因此需要进行该判断 { cout<<" "; } } } else { cout<<-1; } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
二、最小生成树
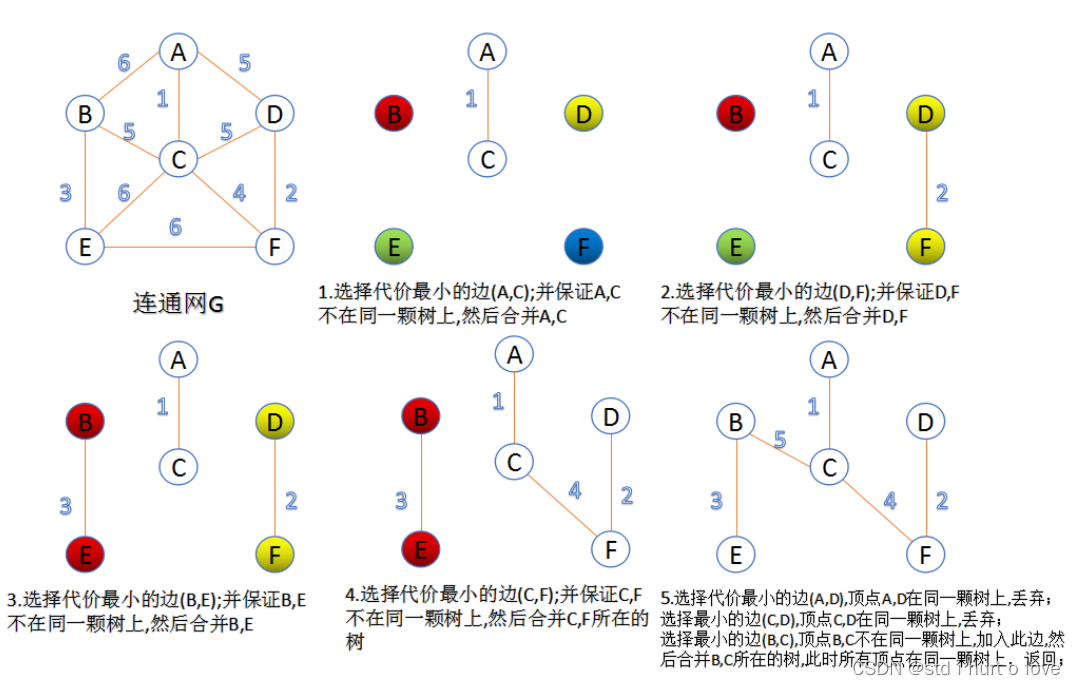
解法一:kruskal算法+并查集
最小生成树,我们可以连通的点看成是同一个并查集,利用并查集的思想来逐渐加边使所有节点连在一起。同时,最小生成树需要用kruskal算法的贪心思想,先对邻接表按照边权递增排序,然后从最小的边开始遍历,检查边的两边是否在同一个并查集中,如果在则不加这条边,如果不在则将这条边加入总边权,同时设置二者属于同一个并查集。
class Solution { public: static bool cmp(vector<int>& x, vector<int>& y){ //重载比较,按照边权递增 return x[2] < y[2]; } int find(vector<int>& parent, int x){ //向上找到最高的父亲 if(parent[x] != x) parent[x] = find(parent, parent[x]); return parent[x]; } int miniSpanningTree(int n, int m, vector<vector<int> >& cost) { vector<int> parent(n + 1); for(int i = 0; i <= n; i++) //初始父亲设置为自己 parent[i] = i; sort(cost.begin(), cost.end(), cmp); //边权递增排序 int res = 0; for(int i = 0; i < cost.size(); i++){ //遍历所有的边,将连通的放入同一个并查集 int x = cost[i][0]; int y = cost[i][1]; int z = cost[i][2]; int px = find(parent, x); //查找x的最上边父亲 int py = find(parent, y); // 查找y的最上边父亲 if(px != py){ //如果二者不在同一个集合 res += z; //边加入 parent[px] = py; //设置二者在同一个集合 } } return res; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
时间复杂度:O(m log 2 \log_2 log2m+nm),排序的复杂度加上最坏情况对于遍历到的每条边都要采用并查集的查找n次
空间复杂度:O(n),记录并查集的数组及递归栈解法二:prim算法
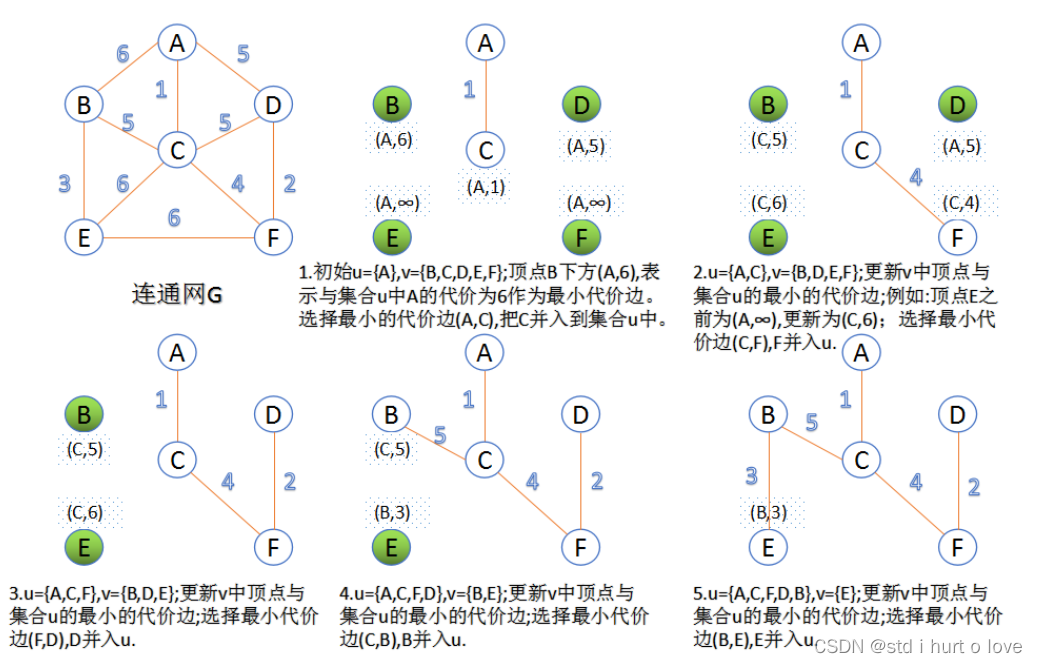
第一次加入最小的边的两点,然后从其中一个点出发每次只加入与这个点相连的最短的边,我们用unordered_set对点进行去重,每次加入一条边,边集合就删去它,直到集合中点的个数为n。(先按边权升序排序,才能每次遇到更短的边。)class Solution { public: static bool cmp(vector<int>& x, vector<int>& y){ //重载比较,按照边权递增 return x[2] < y[2]; } int miniSpanningTree(int n, int m, vector<vector<int> >& cost) { unordered_set<int> points; //记录不重复的点 int res = 0; sort(cost.begin(), cost.end(), cmp); //排序得到最小值 res += cost[0][2]; //首先将最小的边加入 points.insert(cost[0][0]); points.insert(cost[0][1]); while(1){ if(points.size() == n) //所有的点已连通 break; for(auto iter = cost.begin(); iter != cost.end(); iter++){ //从小到大遍历剩余的边 //这个边一个点在集合内,一个不在就加入 if((points.find((*iter)[0]) != points.end() && points.find((*iter)[1]) == points.end()) || (points.find((*iter)[1]) != points.end() && points.find((*iter)[0]) == points.end())){ res += (*iter)[2]; points.insert((*iter)[0]); points.insert((*iter)[1]); cost.erase(iter); //删除该边 break; } } } return res; } };- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
时间复杂度:O(m log 2 \log_2 log2m+nm),排序的复杂度加上最坏情况每个点加入的边都需要遍历数组,删去边的复杂度也为O(n)
空间复杂度:O(n),集合的大小最坏为n -
相关阅读:
DNG格式详解,DNG是什么?为何DNG可以取代RAW统一单反相机、苹果安卓移动端相机拍摄输出原始图像数据标准
Java线程中interrupt,看一个例子都懂了
英语写作中“展示”、“表明”demonstrate、show、indicate、illustrate的用法
Qt 输入组控件(Input Widgets)& 显示组控件(Display Widgets)详解
分布式锁开发
看了这篇不用再苦恼如何将视频压缩了
【Windows】基于curl命令的Shell上线姿势--解决shiro命令执行工具命令回显拉胯的问题
java计算机毕业设计springboot+vue专业手语翻译预约系统
传输层 --- UDP
java计算机毕业设计共享顺风车管理系统MyBatis+系统+LW文档+源码+调试部署
- 原文地址:https://blog.csdn.net/qwer1234mnbv_/article/details/126076814
