-
深度学习基本概念
Liner Model 太过简单,不能拟合复杂的关系
可能出现如下情况:
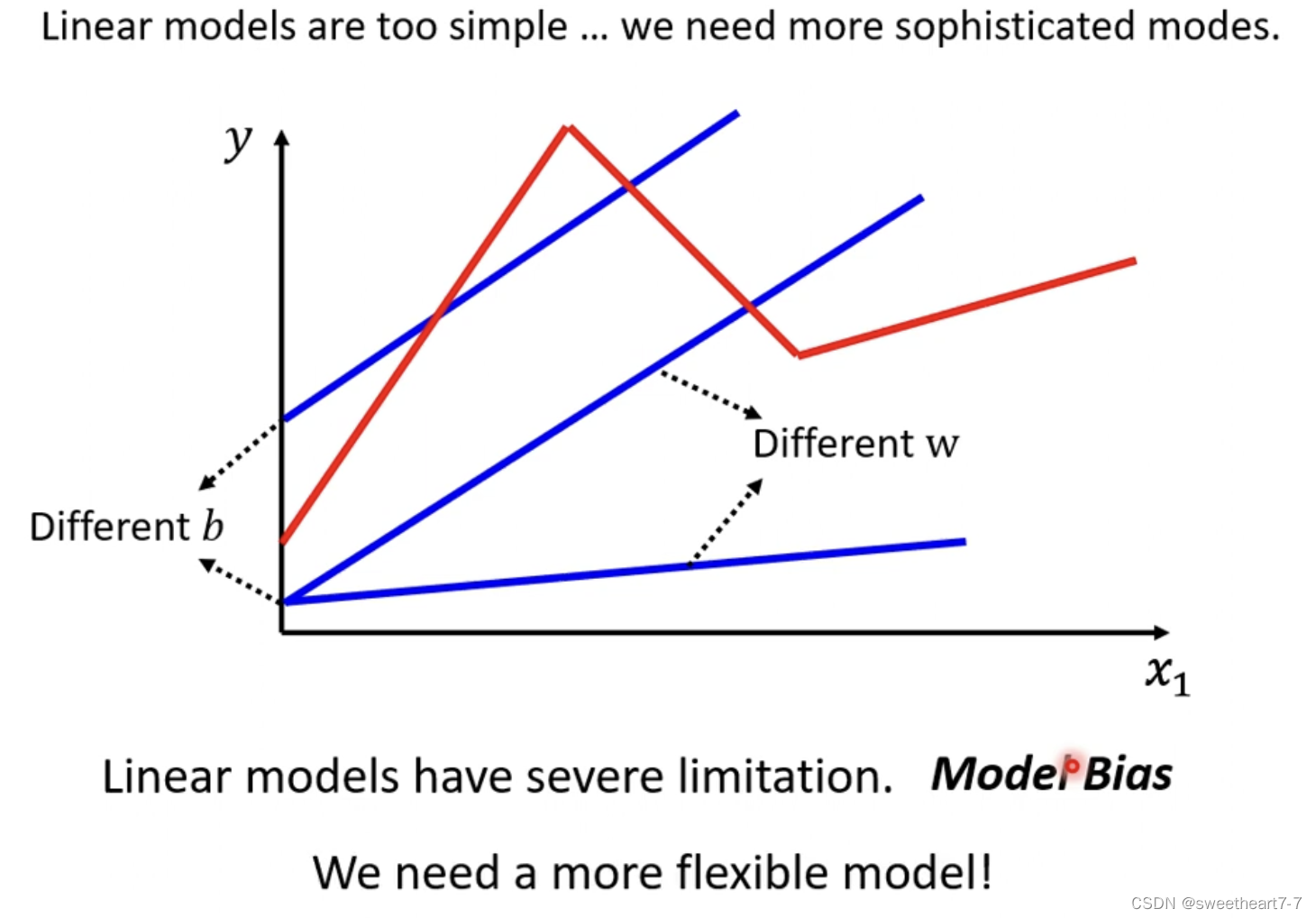
如何写更复杂的有未知参数的函数?
红色function 可以看作 一个常数 + 一群蓝色的function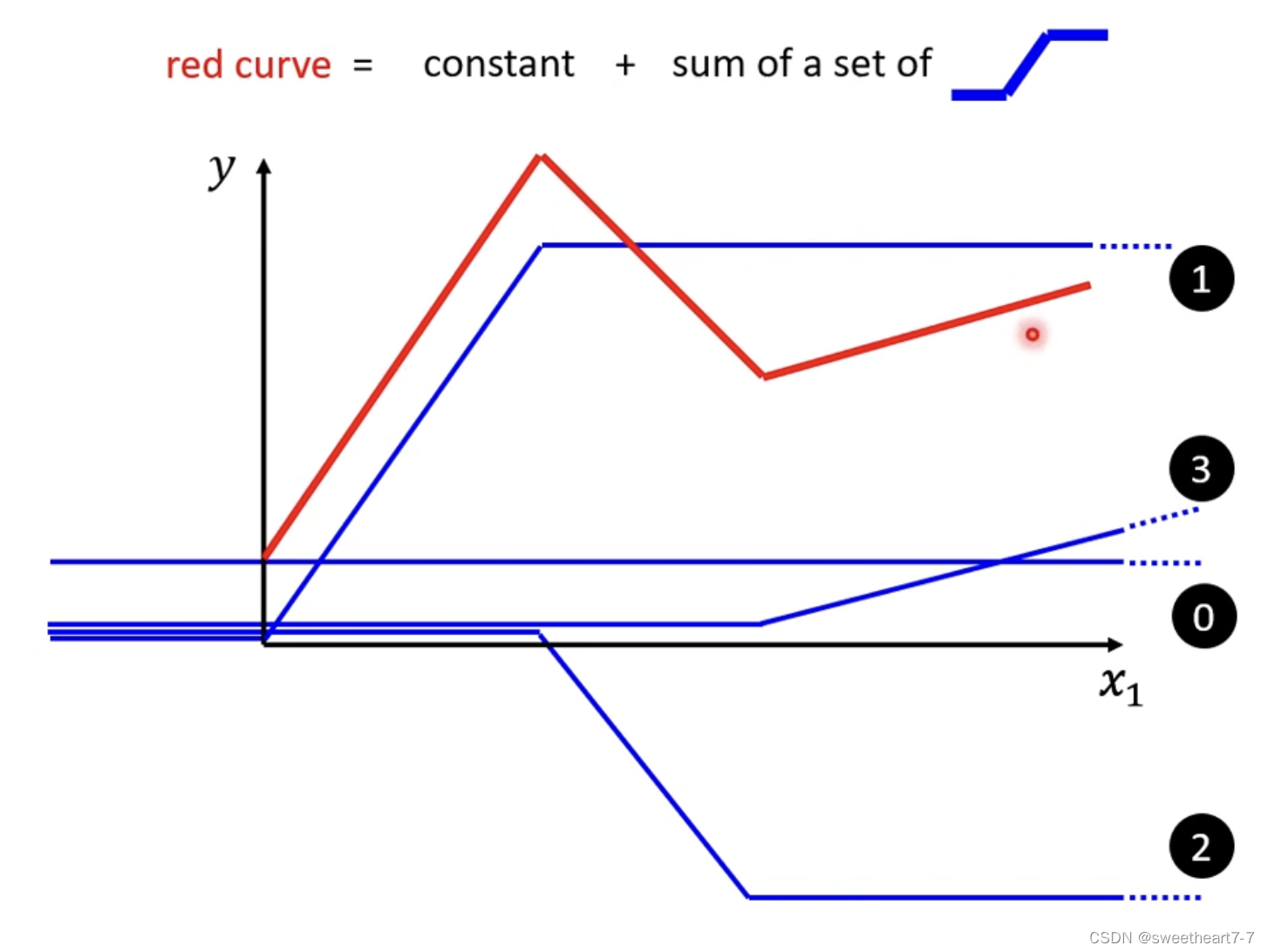
曲线也可以通过取适当的点然后把这些点连接起来形成一个 Piecewise Liner(分段) 的 Curves,所以可以通过足够多的 蓝色的 function 加起来形成任何的曲线。
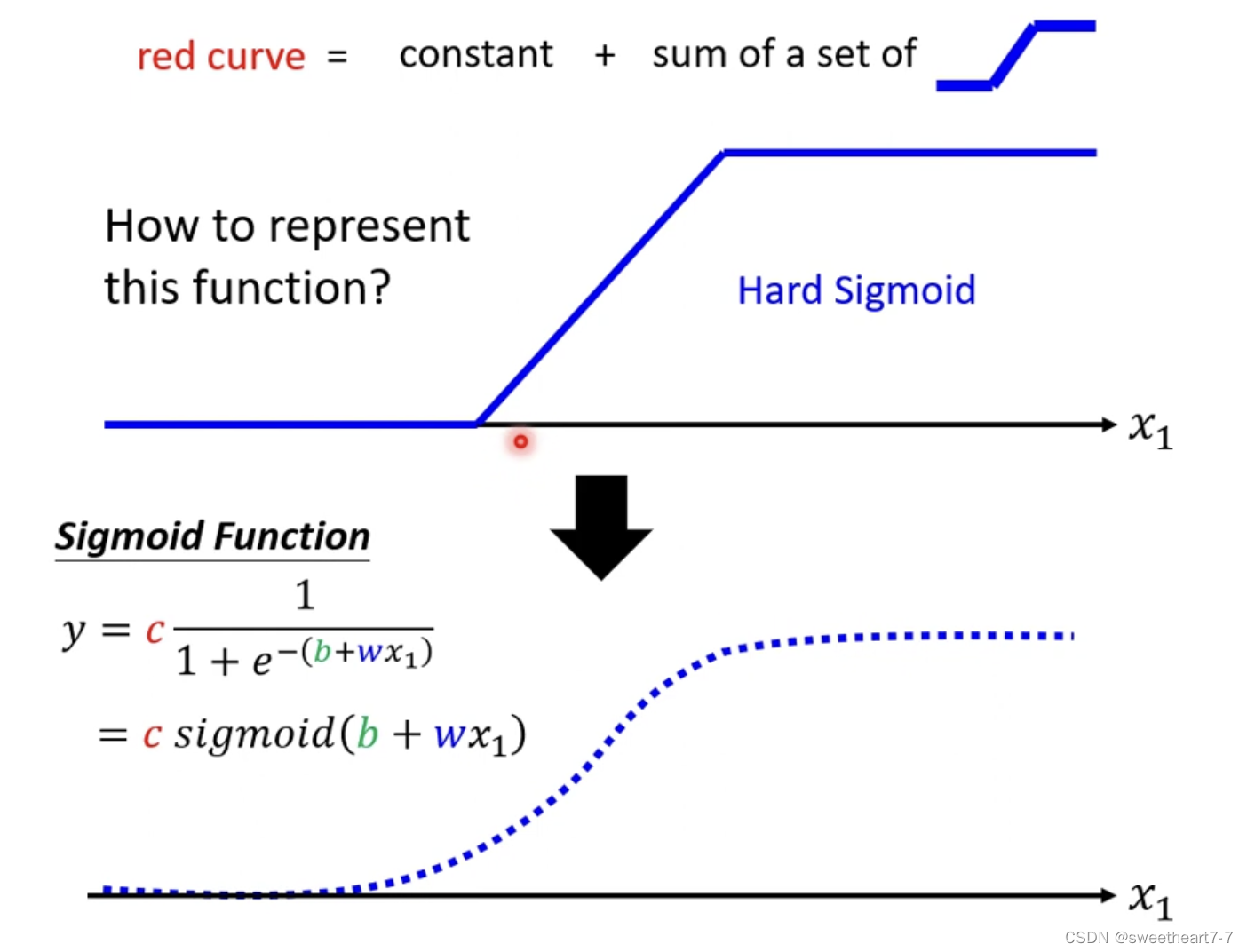
通过 sigmoid function 来逼近 蓝色的 function
sigmoid Function:S 形的 function
y = c 1 1 + e − ( b + w x 1 ) y = c \frac{1}{1 + e^{-(b+wx_1)}} y=c1+e−(b+wx1)1
= c s i g m o i d ( b + w x 1 ) = c ~sigmoid(b+wx_1) =c sigmoid(b+wx1)当 w w w 为正时, x 1 x_1 x1 趋近于 ∞ 时,sigmoid 趋近于 c c c, w w w 为负时,…,sigmoid 趋近于 0 0 0。
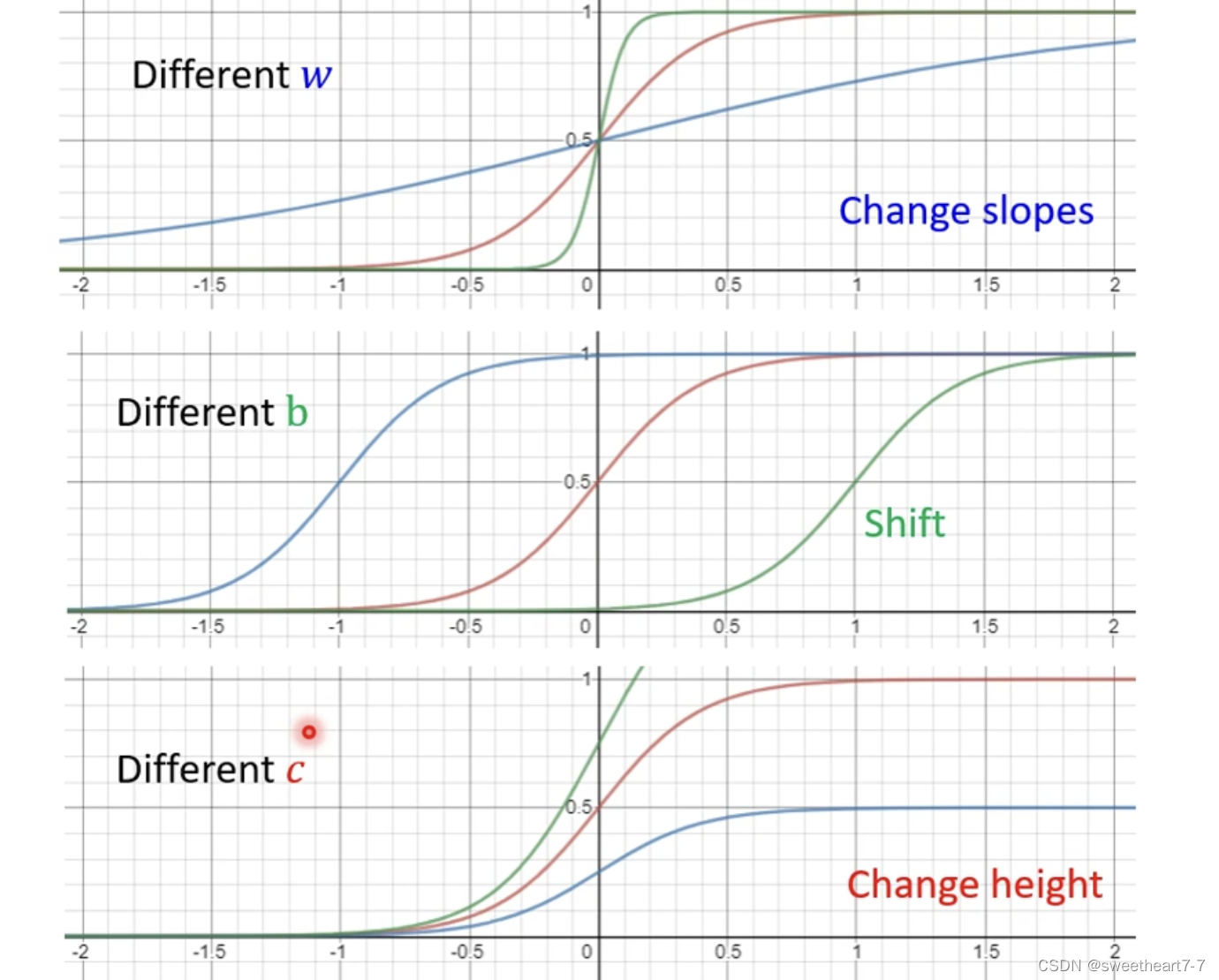
通过调整 w w w、 b b b 和 c c c 来得到各种形状的 sigmoid function 来拟合各种蓝色的 function。
所以 0、1、2、3 这 4 条蓝色的 function 都可以用 c s i g m o i d ( b + w x 1 ) c sigmoid(b + wx_1) csigmoid(b+wx1) 来表示,只是对应的 c c c、 w w w 和 b b b 不同,所以红色的 function y y y 就可以用以下形式表示:

所以可以通过 调整 c i c_i ci、 b i b_i bi 和 w i w_i wi 来拟合各种各样曲线的 function有弹性的有未知参数 function
从 线性的 y = b + w x 1 y=b + wx_1 y=b+wx1
推广到 分段 曲线 function
y = b + ∑ i c i s i g m o i d ( b i + w i x 1 ) y = b + \sum_{i}c_i~sigmoid(b_i+w_ix_1) y=b+∑ici sigmoid(bi+wix1)这里只有 x 1 x_1 x1 代表只能通过当前一条数据结果来预测下一个结果。
而 在上一个 blog 最后 推广到可能具有周期性,所以可以通过 多个 feature 来改造函数,然后再对具有多个 feature 的函数进行推广,就有
y = b + ∑ j w j x j y = b + \sum_{j}w_jx_j y=b+∑jwjxj 推广为
y = b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) y = b + \sum_{i}c_i~sigmoid(b_i+\sum_{j}w_{ij}x_j) y=b+∑ici sigmoid(bi+∑jwijxj)相当于从多个 feature 与 y y y 有一个线性关系推广为多个 feature 与 y y y 有一个曲线关系
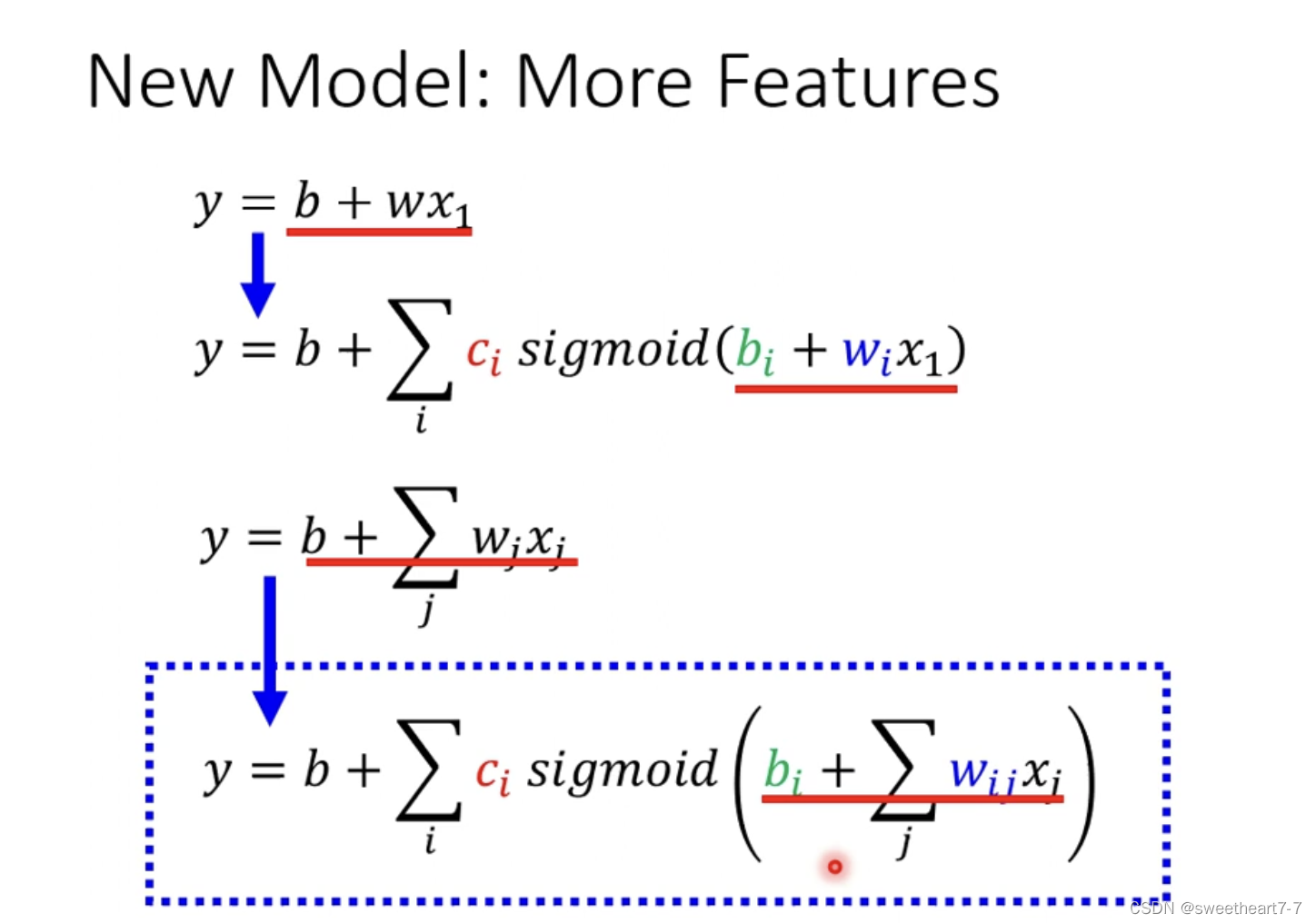
i i i 代表多个 s i g m o i d 函数 sigmoid函数 sigmoid函数,而 j j j 代表多个featurew i j w_{ij} wij 表示 再 第 i i i 个 sigmoid 里面乘 给 第 j j j 个 feature 的 w e i g h t weight weight
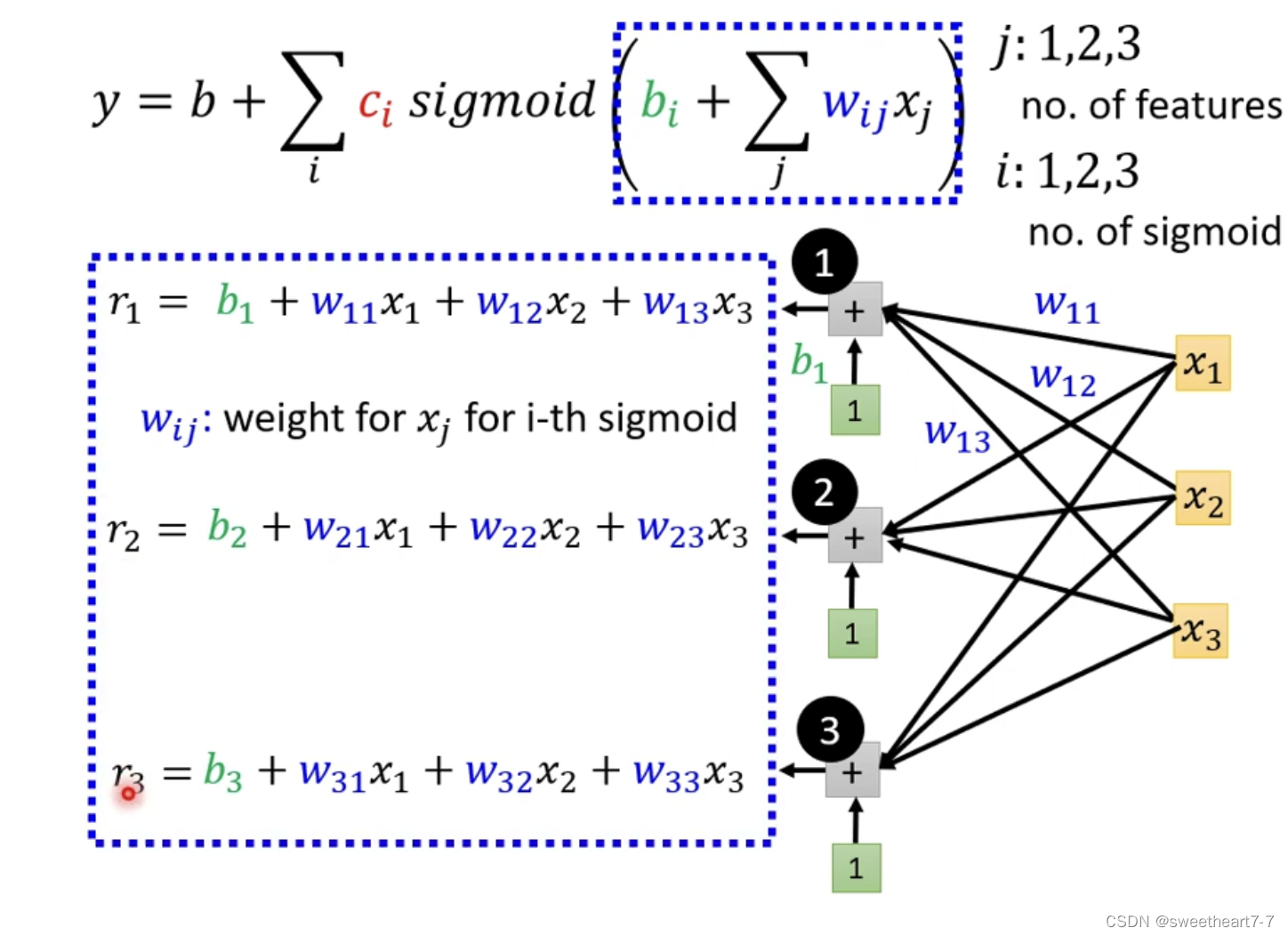
可以用以下向量与矩阵关系表示这个乘法关系

所以 a 1 = s i g m o i d ( r 1 ) = 1 1 + e − r 1 a_1 = sigmoid(r_1) = \frac{1}{1+e^{-r_{1}}} a1=sigmoid(r1)=1+e−r11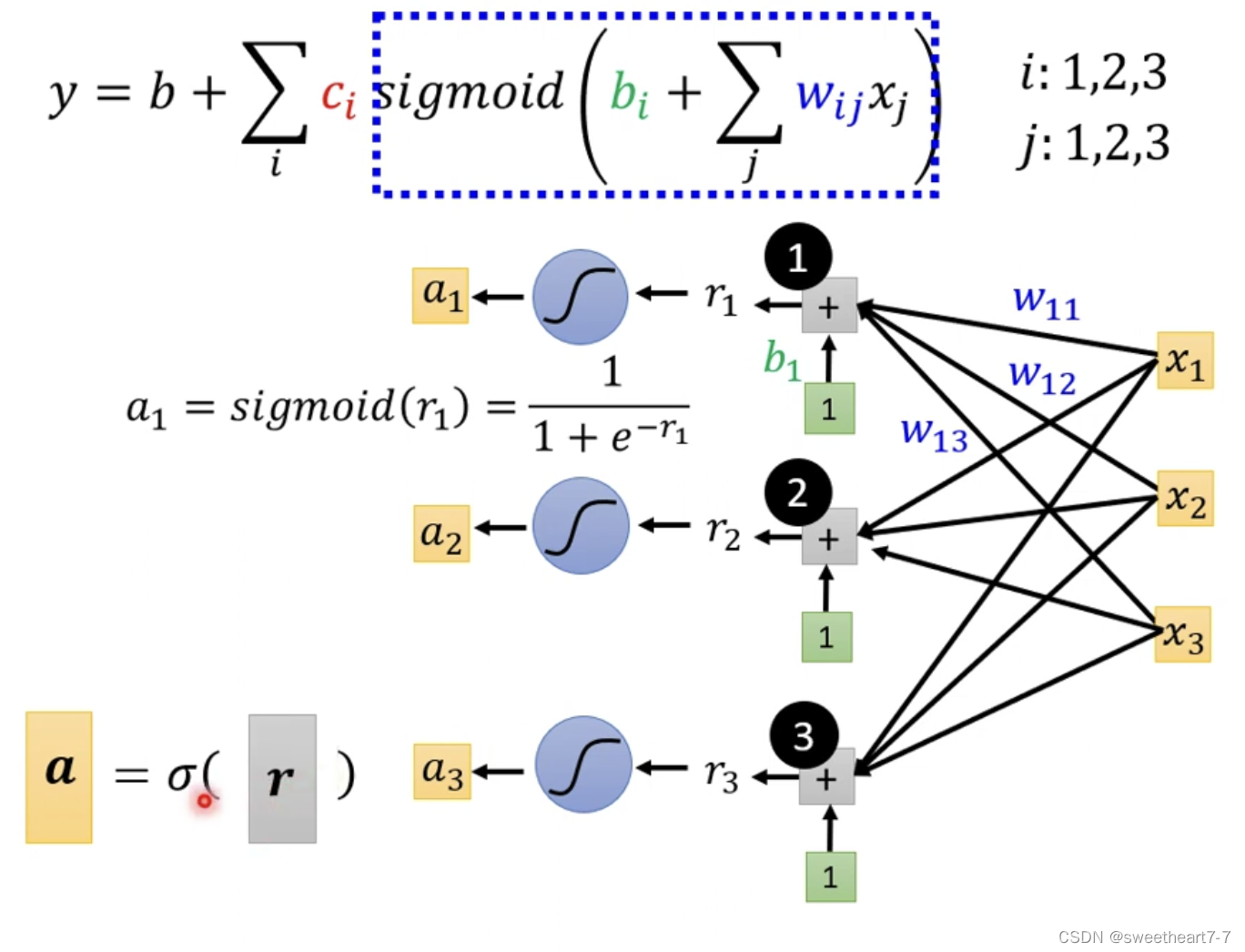

所以用线性代数表示为:

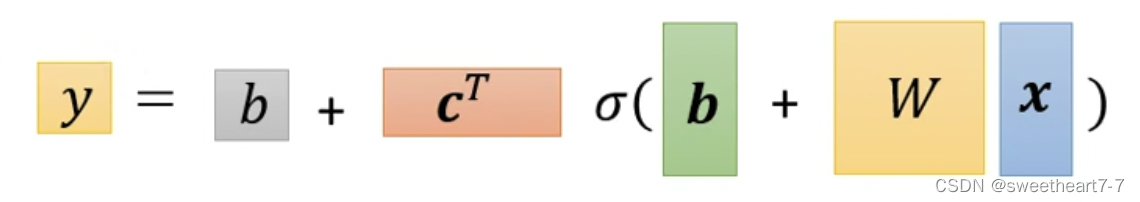

将未知参数 W W W、 b 向量 b向量 b向量、 C T 向量 C^T向量 CT向量、 b 常数 b常数 b常数展开成 θ θ θ 向量这样就完成了 ML 的第一步

Loss 还是同样的方法,带入一组 θ θ θ 然后求得 y y y 并且求与 y ^ \hat{y} y^ 的差值,来判断这组 θ θ θ 的好坏。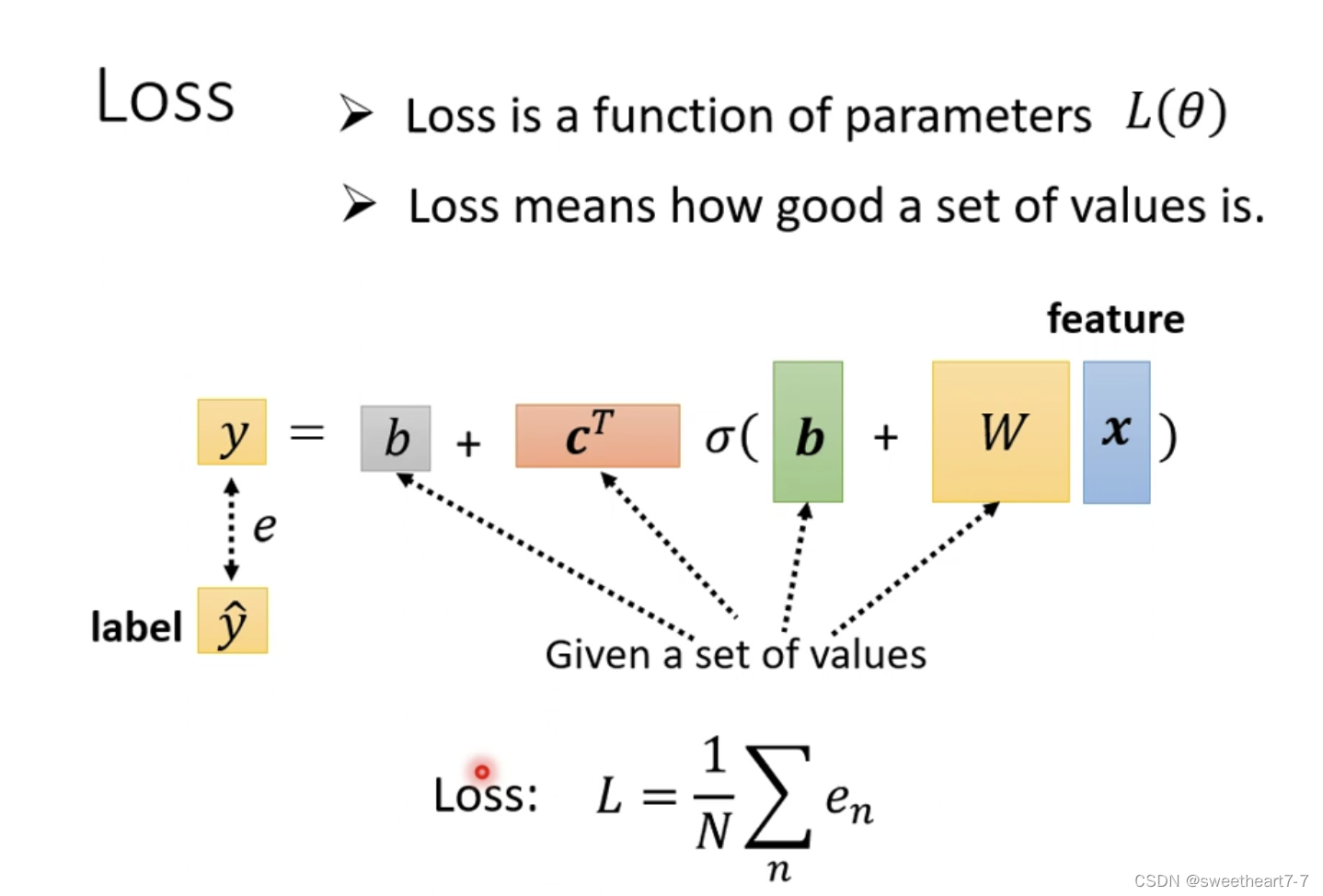
第三步 Optimization 的方法也没有变化对所有的 θ i θ_i θi 求 微分,然后得到一个向量 g g g
g g g 就是 gradient

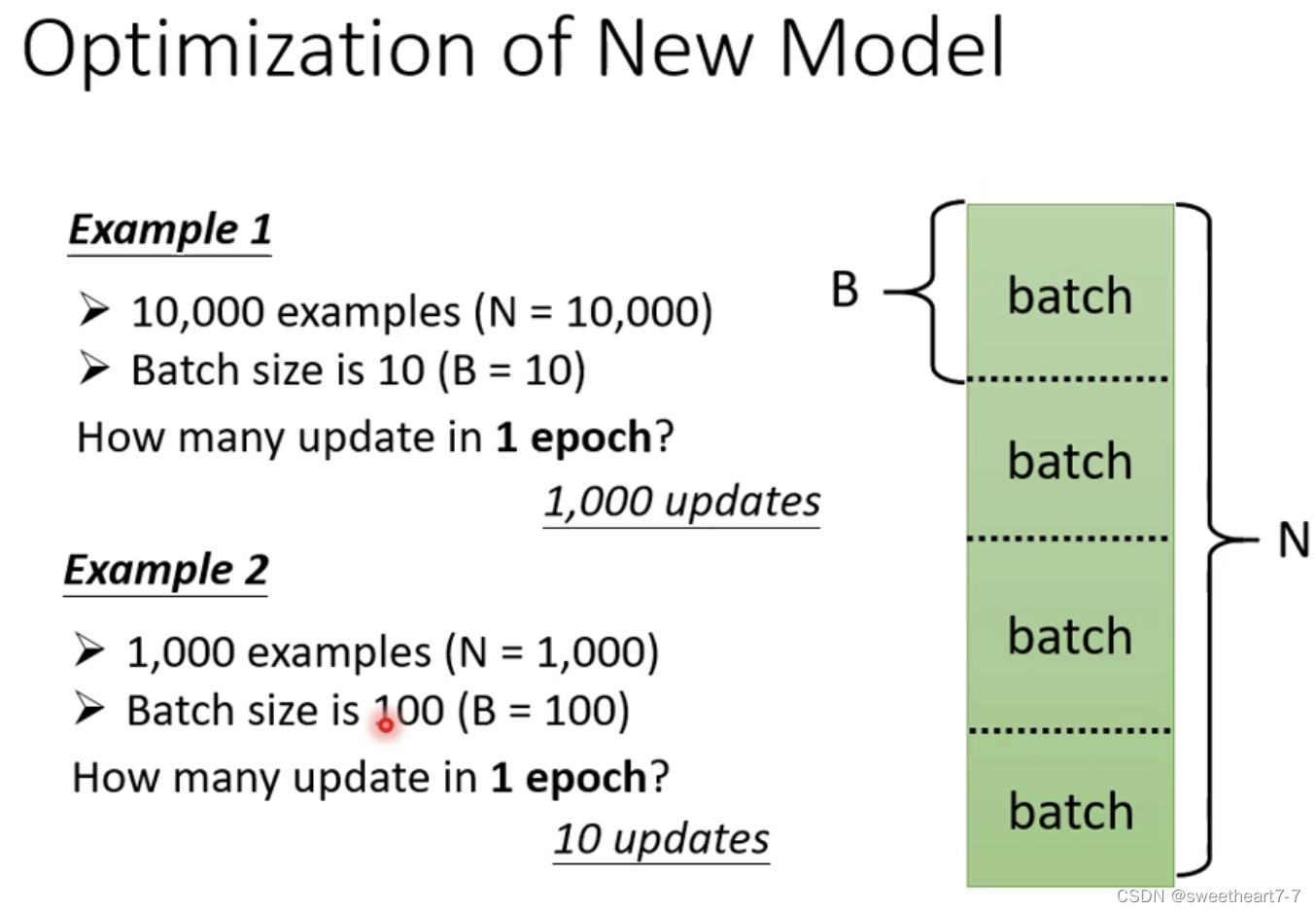
在实际的程序中,需要把大 data 随机分成多个 batch,然后对每一个 batch 进行计算 g g g,更新 θ θ θ(一个 epoch),每一次更新参数(一个batch)叫做一次 update
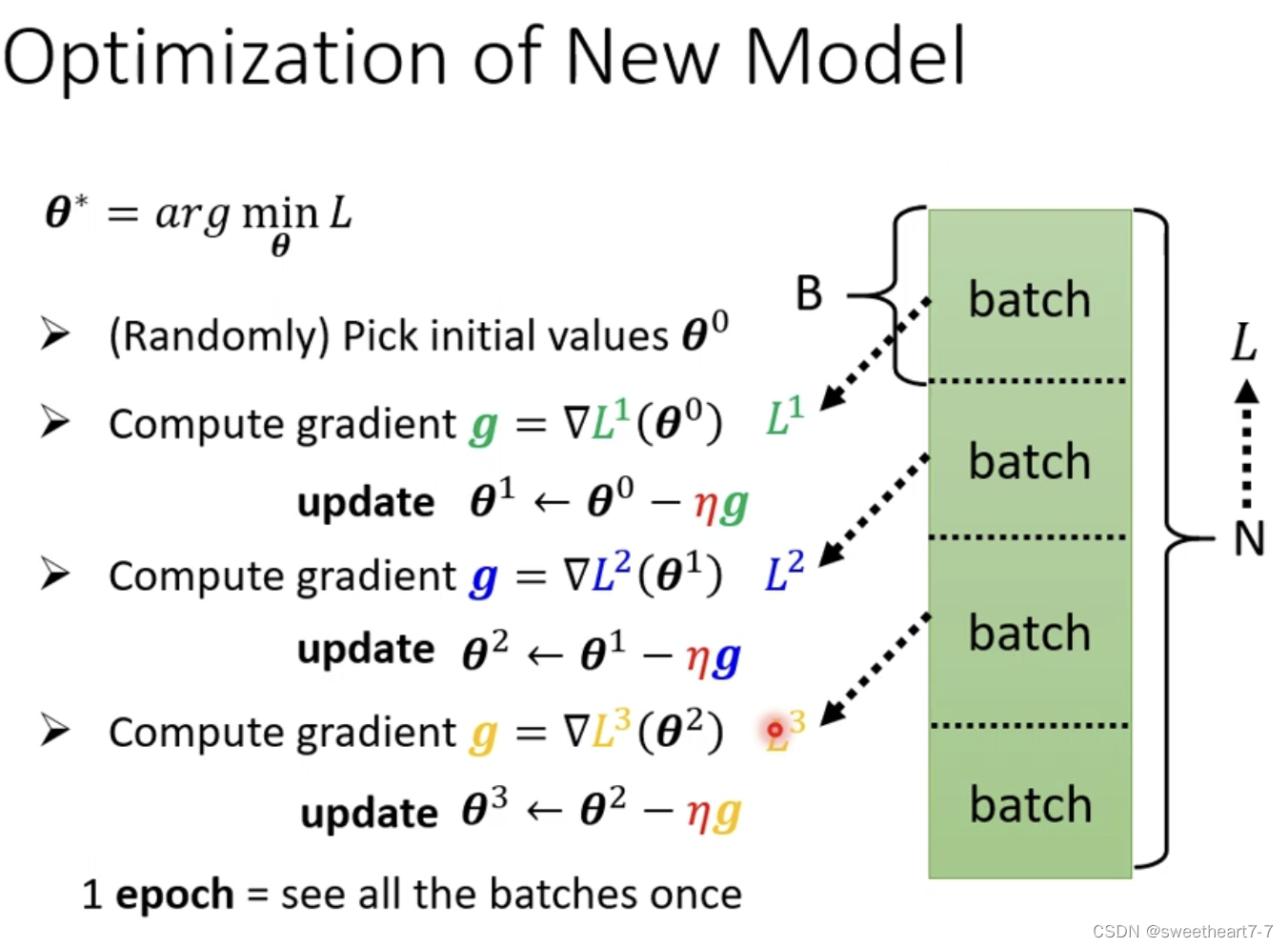
batchsize 也是 hyperparameter
通过 Relu 来逼近 蓝色的 function
需要先用 Relu 拟合 Hard sigmoid
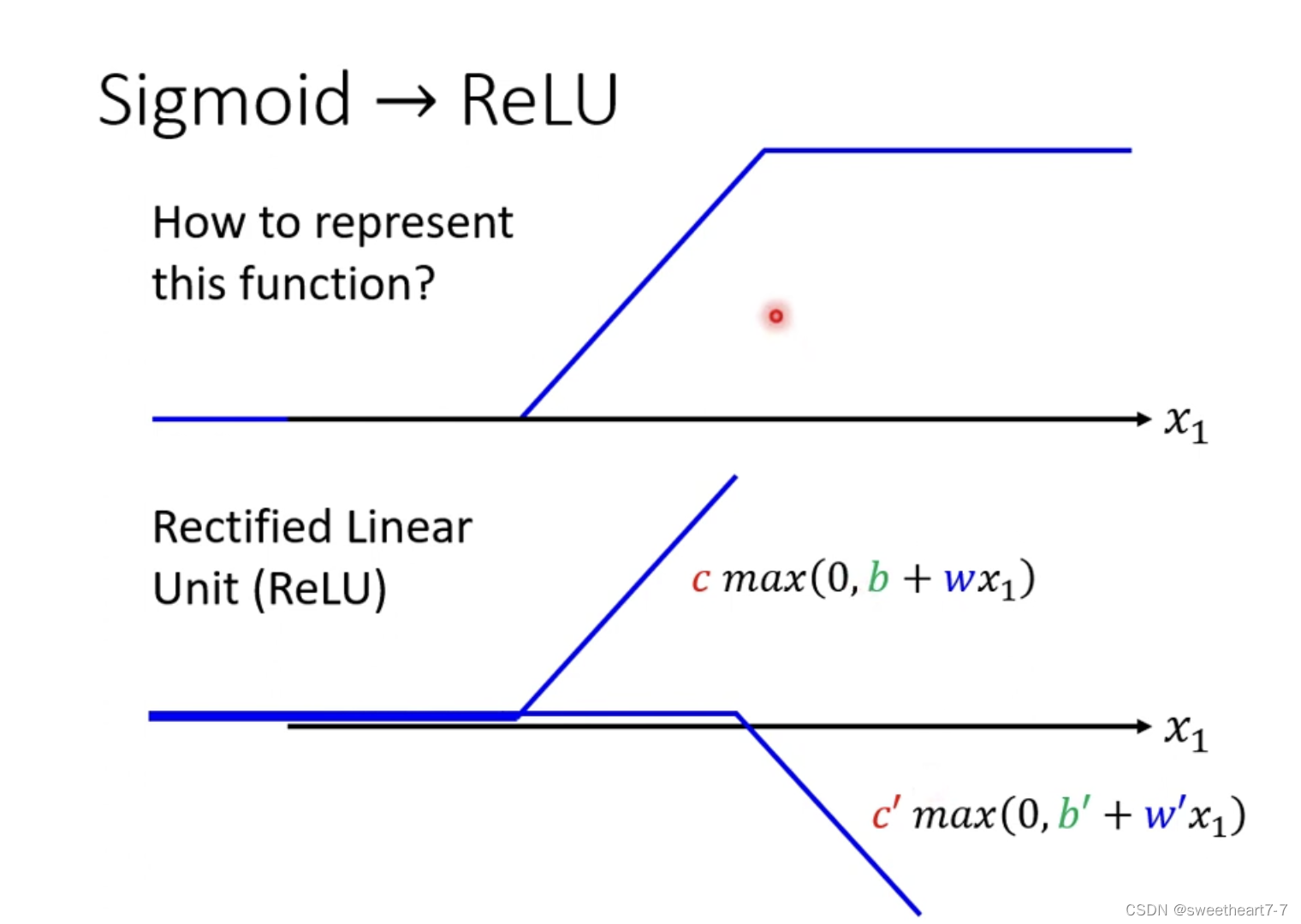
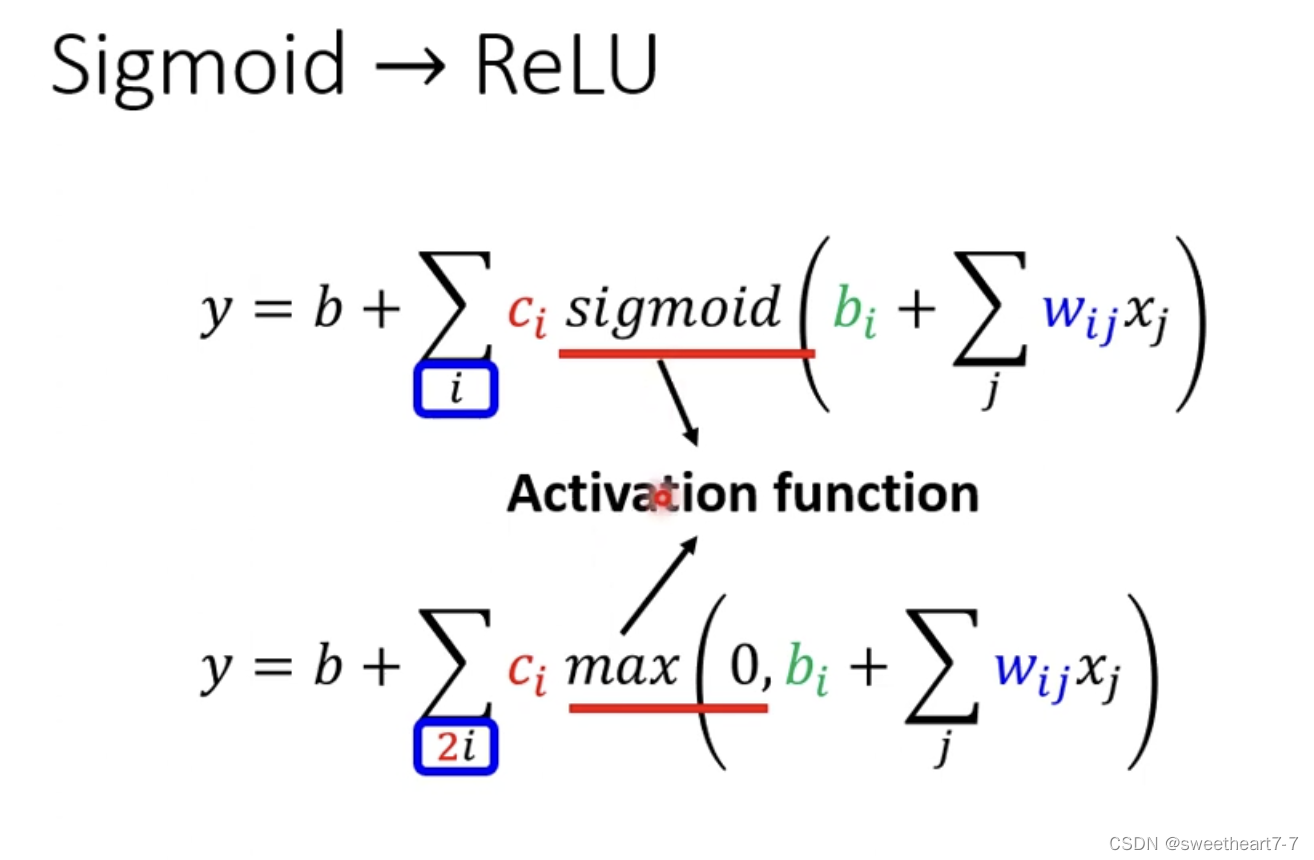
sigmoid 与 Relu 统称为 activation function我们可以重复多次 进行如下扩展:
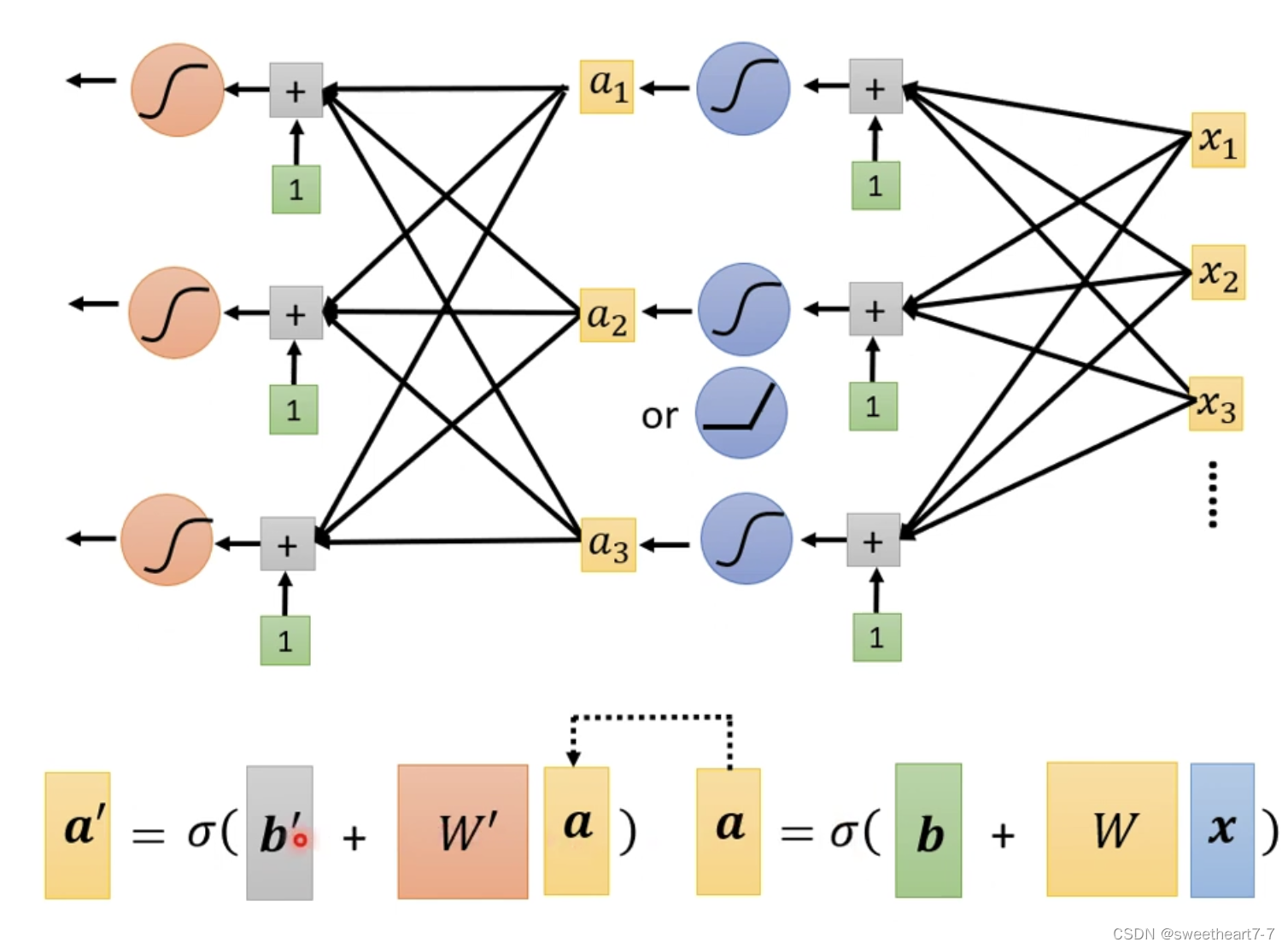
多个 layer
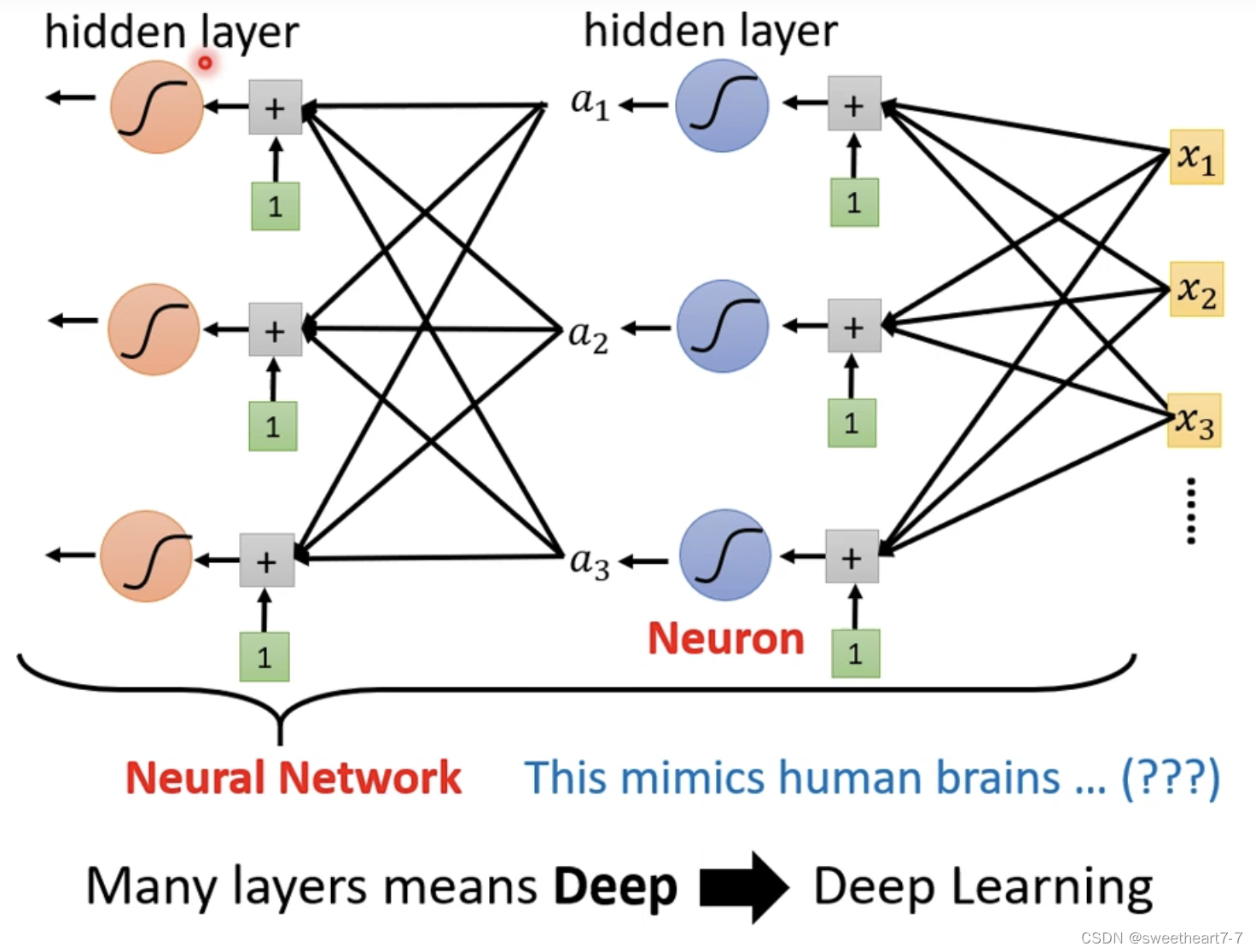
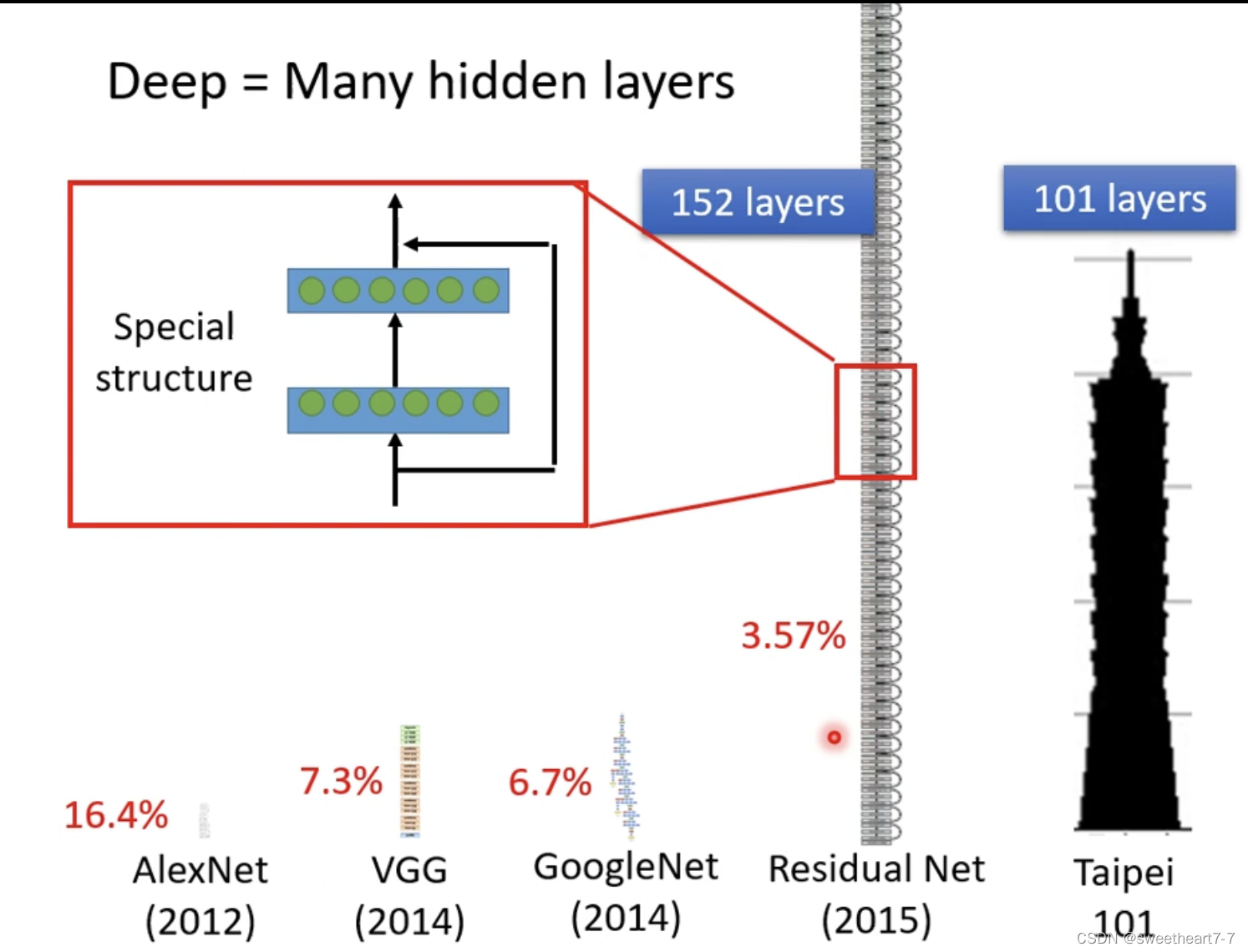
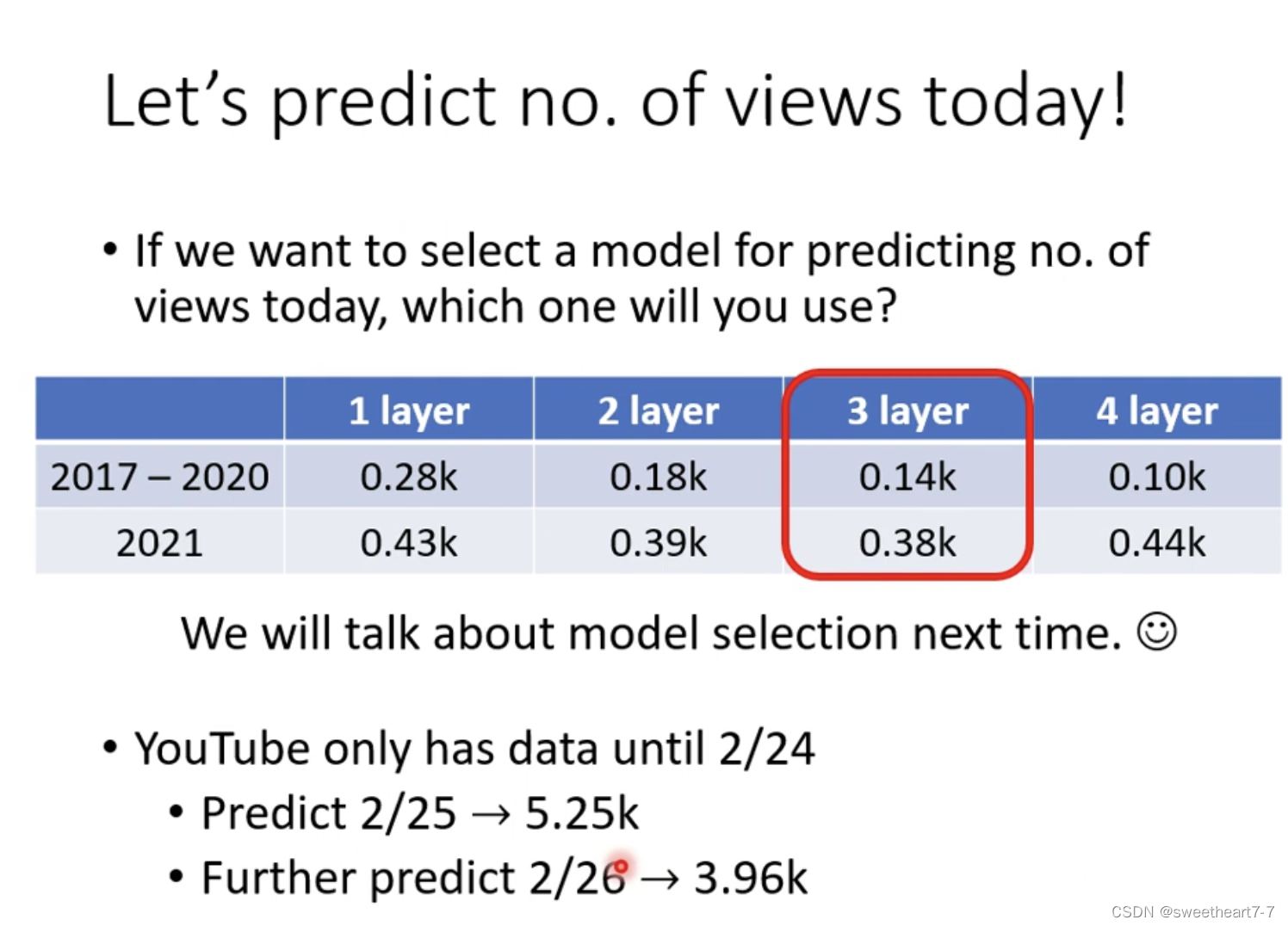
-
相关阅读:
抖音视频评论采集软件|抖音数据抓取工具
堆 AcWing 838. 堆排序
使用Python将MP4视频转换为图像
shell编程基础
1011 A + B 和 C【PAT (Basic Level) Practice (中文)】
二、CSS下拉菜单[颜色布局、子影响父]
Nginx gateway集群和动态网关
shell脚本之免交互
etcd迁移
视觉slam论文、代码汇总
- 原文地址:https://blog.csdn.net/qq_46456049/article/details/126073965