并查集的应用

leetcode：952.按公因数计算最大组件大小

题目描述：
给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。

返回 图中最大连通组件的大小 。

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

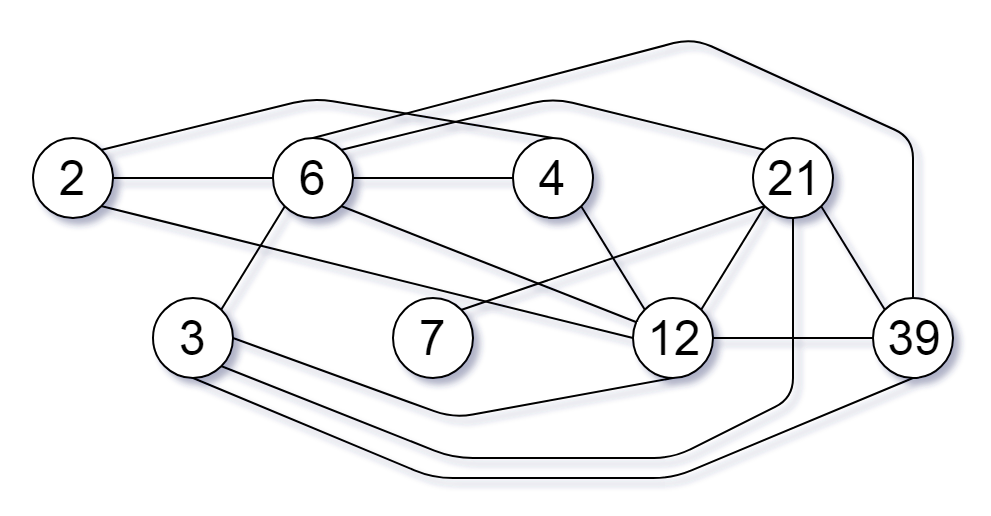
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

提示：
1 <= nums.length <= 2 * 10^4
1 <= nums[i] <= 10^5
nums 中所有值都 不同

解法：

class Union:
    def __init__(self, n: int):
        self.parents = list(range(n))  # 父节点
        self.height = [0] * n          # 树的高度

    def find(self, x) -> int:
        """if self.parents[x] != x:
            self.parents[x] = self.find(self.parents[x])
        return self.parents[x]"""
        parent = self.parents[x]
        while self.parents[parent] != parent:
            parent = self.parents[parent]
        return parent

    def merge(self, x: int, y: int) -> None:
        x, y = self.find(x), self.find(y)
        if x == y:
            return 
        elif self.height[x] > self.height[y]:
            self.parents[y] = x
        elif self.height[x] < self.height[y]:
            self.parents[x] = y
        else:
            self.parents[y] = x
            self.height[x] += 1

class Solution:
    def largestComponentSize(self, nums: List[int]) -> int:


        # 方法一：并查集
        # 时间复杂度：O(n * alpha(n) * m**0.5)
        # 空间复杂度：O(m)
        # alpha()为反阿克曼函数
        # m = max(nums)
        union = Union(max(nums) + 1)
        for num in nums:
            i = 2
            while i * i <= num:
                if num % i == 0:
                    union.merge(num, i)
                    union.merge(num, num // i)
                i += 1

        #print(union.parents)
        #print(union.height)
        #print(Counter(union.find(num) for num in nums))
        return max(Counter(union.find(num) for num in nums).values())

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49