一. 判别模型(Discriminative Model)

1. 支持向量机(SVM, Supported Vector Machine)

使用松弛变量来处理噪声。
将低维空间线性不可分问题转化为高维空间线性可分问题。

2. 神经网络(NN, Neural Network)

3. 线性判别分析(Linear Discriminant Analysis, LDA)

现在用作判别很少了，一般作为一种有监督降维方法。对所有样本进行一次线性变换，降低维度。线性变换矩阵通过求去前k个特征值对应的特征向量得到。

4. 线性回归(Linear Regression)

Y=AX+B
回归A和B的值。
参数估计方法使用最小二乘法

5. 逻辑回归(Logistics Regression)

逻辑回归解决的是分类问题。
参数估计方法使用极大似然法。
与线性回归的区别是将输出通过Sigmoid归到0-1之间，同样也是用MSE均方差损失，在inference时候用阈值0.5来判断。

6. 高斯过程(Gaussian Process)

7. 条件随机场(CRF, Conditional Random Field)

8. CART(Classification and Regression Tree)

9. Boosting增强学习

梯度提升树(Gradient Boosting Decision Tree，GBDT)
和随机森林类似，也是训练一堆决策树，不同之处在于GBDT采用所有样本来进行训练，同时决策树的训练是串行的，下一棵训练的决策树是用于拟合上一棵决策树的输出和标签的偏差。
XGBoost(Experience Gradient Boosting)
XGBoost是GBDT的优秀版本。
两个提升：
1.考虑二阶梯度，摆脱对GBDT偏差的依赖，实现并行。
XGBoost目标函数如下所示，包含损失函数和正则项两部分。
损失函数中yi为标签，^yi为上一个决策树预测结果,ft(xi)为该决策树输出结果。

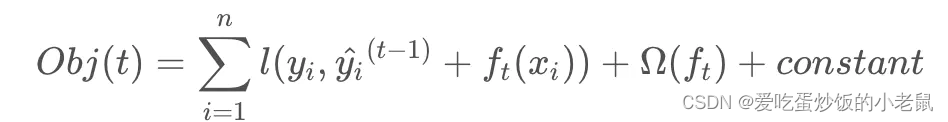
将上式与泰勒展开式对比

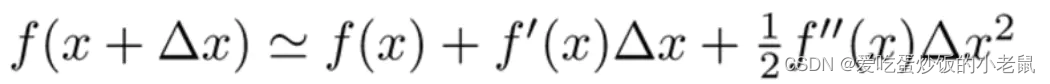
ft(xi)就是Δx，故损失函数可以展开为

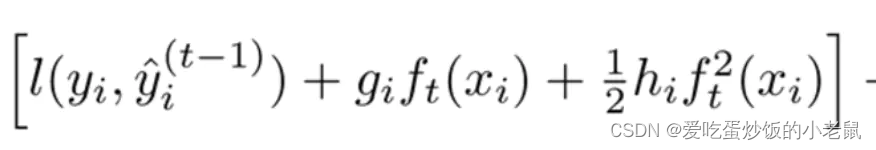
其中

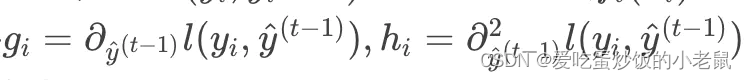
2.使用正则项分裂方法限制了决策树叶子节点数量。
精确贪心算法：可以找到精确的划分条件，但计算量大、内存消耗大、容易过拟合。
Level-wise预排序方法
LightGBM
GBDT的另一个改进版本，改进了XGBoost。
XGBoost的不足
a）每轮迭代时，都需要遍历整个训练数据多次，如果把整个训练数据装进内存，则会限制训练数据的大小，如果不装进内存，反复读写训练数据又会消耗非常大的时间。
b）预排序方法的时间和空间的消耗都很大。
LightGBM原理
1）直方图算法：把连续的浮点特征值离散化成k个整数，同时构造一个宽度为k的直方图。当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。在XGBoost中需要遍历所有离散化的值，而在这里只要通过遍历k个直方图的值
2）LightGBM的直方图做差加速：一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到，且直方图做差仅遍历直方图的k个桶
3）带深度限制的leaf-wise的叶子生长策略
4）直接支持类别特征（即不需要组偶one-hot编码）
5）支持高效并行：
a）特征并行：在不同机器在不同的特征集合上分别寻找最优的分割点，然后在机器间同步最优分割点
b）数据并行：让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点
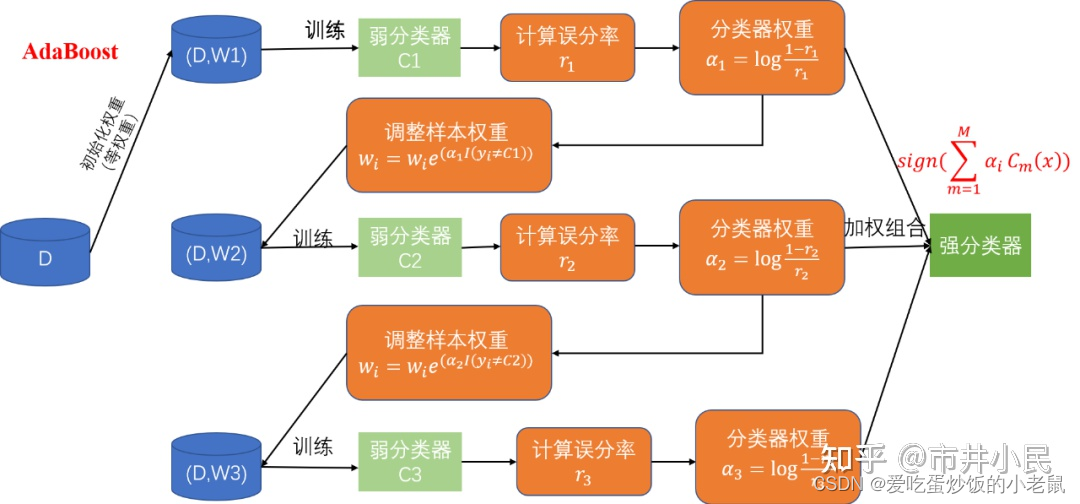
AdaBoost(Adaptive Boosting)
问题：类似随机森林的一堆弱分类器性能都很弱，即使一起预测，对于一些困难样本仍然难以正确预测。故AdaBoost使用Boosting方法，让下一个决策树着重于上一个决策树未正确分类的部分。
AdaBoost是Adaptive Boosting（自适应增强）的缩写，它的自适应在于：被前一个基本分类器误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或预先指定的最大迭代次数再确定最后的强分类器。

10. 决策树(Decision Tree)

纯度：种类越少，纯度越高。
熵：熵衡量样本的混乱程度，熵越大，纯度越小，熵越少，纯度越高。
信息增益：熵降低的越多，所包含的信息量越大，信息增益的就越多。
信息增益率：从ID3到C4.5的改进。
ID3、C4.5、C5.0、CART
ID3选用使得信息增益最大的那个属性来划分样本，对于取值很多的属性，具有每个取值的样本只有1个或很少(如客户ID)，信息增益会很高。故ID3倾向于挑选取值较多的分类属性来划分。像这种使用客户ID这种自变量的划分是没有意义的，会造成过拟合。而ID3并没有任何防止过拟合的措施。

C4.5
针对ID3倾向于挑选值较多的属性划分导致过拟合的问题，使用信息增益比代替信息增益作为划分标准。
CART(classification and regression tree)使用使得gini系数最小的那个属性来划分样本。
CART与C4.5算法是非常相似的，但是CART支持预测连续的值（即回归）。
CART构建二叉树，而C4.5则不一定。显然由于二叉树的原因使得CART5不会出现ID3的问题（倾向于选择属性值多的属性来划分样本）
CART用训练集和交叉验证集不断地评估决策树的性能来修剪决策树，从而使训练误差和测试误差达到一个很好地平衡点。

11. 随机森林

随机对样本和特征进行抽样，并行独立地训练很多棵决策树，每个决策树的训练目标都是高偏差低方差的(欠拟合)，用这些弱分类器预测结果求均值(Bagging)来获得最终结果。

11. KNN(K-nearest Neighbors)

KNN的原理就是当预测一个新的值x的时候，根据它距离最近的K个点是什么类别来判断x属于哪个类别。

12. 最大熵模型

二、生成模型

1. 朴素贝叶斯(Naive Bayes)

贝叶斯的假设/前提为特征变量之间相互独立。
贝叶斯公式：
$P(类别|特征)=\frac{P(特征|类别)P(类别)}{P(特征)}$
对于要预测的样本根据特征计算对各个类别计算概率，最大的$P(类别|特征)$对应的类别即为预测分类的类别。
出现未知特征时候，P(特征|类别)=0，会出现分类错误，可采用拉普拉斯平滑，对各种特征的次数+1后计算概率。
优点：算法逻辑简单,易于实现；分类过程中时空开销小。
缺点：属性个数比较多或者属性之间相关性较大时，分类效果不好。

2. 混合多项式

3. 混合高斯模型

4. 专家混合模型(Mixture of Experts Model)

5. 隐马尔可夫模型(HMM)

6. 马尔可夫随机场(Markov Random Fields)

马尔可夫随机场(Markov random field),又称为概率无向图模型， 是一个可以由无向图表示的联合概率分布。

7. Sigmoid Belief Networks

8. 深度信念网络(DBN)

9. 隐含狄利克雷分布(Latent Dirichlet Allocation, LDA)/文档主题生成模型

LDA将文档