机器学习预备知识

1. 维度灾难

维度灾难是指随着数据维度变大（即特征变多），需要的数据就越多，才能使算法起作用。

原因

单位超球体体积 $v_n=(2\pi /n)v_{n-1}$ ，n位球体维度

可见，随着维度变大，单位球体体积趋近0，也就是说距离对数据的影响越来越小，这就使得维度高时，只有大量的数据，才能帮助算法更好地生效

2. 训练、测试、验证集

一个形象的比喻：

训练集：学生的课本，学生根据课本中的内容来掌握知识；

验证集：作业，通过作业可以知道学生的学习情况、进步快慢；

测试集：考试，考题都是平时没见过的，考察学生举一反三的能力。

训练集和测试集大家不陌生，主要是验证集用来做什么要了解下。

验证集

我们让模型在训练集上进行训练，然后在测试集上来近似模型的泛化能力。我们如果想要挑选不同的模型的话，可以让两个模型分别在训练集上训练，然后将两个训练好的模型分别在测试集上进行测试，由于我们把测试集上的误差近似近似为泛化误差，所以我们自然可以选择在测试集上误差小的模型作为最终我们要选择的泛化能力强的模型。

但是我们要做的不仅是不同的模型与模型之间的对比，很多时候我们需要对模型本身进行选择，假如我们有两个模型，线性模型和神经网络模型，我们知道神经网络的泛化能力要比线性模型要强，我们选择了神经网络模型，但是神经网络中还有很多的需要人工进行选择的参数，比如神经网络的层数和每层神经网络的神经元个数以及正则化的一些参数等等，我们将这些参数称为超参数。这些参数不同选择对模型最终的效果也很重要，我们在开发模型的时候总是需要调节这些超参数。

现在我们需要调节这些超参数来使得模型泛化能力最强。我们使用测试集来作为泛化误差估计，而我们最终的目的就是选择泛化能力强的模型，那么我们可以直接通过模型在测试集上的误差来调节这些参数不就可以了。可能模型在测试集上的误差为0，但是你拿着这样的模型去部署到真实场景中去使用的话，效果可能会非常差。

这一现象叫做信息泄露。我们使用测试集作为泛化误差的近似，所以不到最后是不能将测试集的信息泄露出去的，就好比考试一样，我们平时做的题相当于训练集，测试集相当于最终的考试，我们通过最终的考试来检验我们最终的学习能力，将测试集信息泄露出去，相当于学生提前知道了考试题目，那最后再考这些提前知道的考试题目，当然代表不了什么，你在最后的考试中得再高的分数，也不能代表你学习能力强。而如果通过测试集来调节模型，相当于不仅知道了考试的题目，学生还都学会怎么做这些题了（因为我们肯定会人为的让模型在测试集上的误差最小，因为这是你调整超参数的目的），那再拿这些题考试的话，人人都有可能考满分，但是并没有起到检测学生学习能力的作用。原来我们通过测试集来近似泛化误差，也就是通过考试来检验学生的学习能力，但是由于信息泄露，此时的测试集即考试无任何意义，现实中可能学生的能力很差。所以，我们在学习的时候，老师会准备一些小测试来帮助我们查缺补漏，这些小测试也就是要说的验证集。我们通过验证集来作为调整模型的依据，这样不至于将测试集中的信息泄露。

所以：验证集通常用于调整超参数，根据几组模型验证集上的表现决定哪组超参数拥有最好的性能。
同时验证集在训练过程中还可以用来监控模型是否发生过拟合，一般来说验证集表现稳定后，若继续训练，训练集表现还会继续上升，但是验证集会出现不升反降的情况，这样一般就发生了过拟合。所以验证集也用来判断何时停止训练

training :validation : test:数据比例:

• 数据超大：98:1:1（吴恩达）
• 数据充足时：50:25:25
• 数据不足时（万级别以下）：60:20:20
• 数据极少时：留出法，交叉验证法

作用总结：

• train set – 训练模型、确定模型参数
• validation set – 模型选择、超参数优化
• test set – 测试模型泛化性能

3. 留出法、交叉验证法、自助法

3.1 留出法 hand-out

留出法直接将数据集划分为两个互斥的部分，其中一部分作为训练集，另一部分用作测试集。

通常训练集和测试集的比例为70%：30%。同时，训练集测试集的划分有两个注意事项：

1. 尽可能保持数据分布的一致性。避免因数据划分过程引入的额外偏差而对最终结果产生影响。在分类任务中，保留类别比例的采样方法称为“分层采样”（stratified
   sampling）。
2. 采用若干次随机划分避免单次使用留出法的不稳定性。

3.2 交叉验证法 leave-some-out cross-validation

D = D 1 ∪ D 2 ∪ ⋯ ∪ D k D i ∩ D j = ∅

​D=D1​∪D2​∪⋯∪Dk​Di​∩Dj​=∅​
将数据集粗略地分为比较均等不相交的k份，然后取其中的一份进行测试，另外的k-1份进行训练，然后求得error的平均值作为最终的评价，具体算法流程西瓜书中的插图如下：

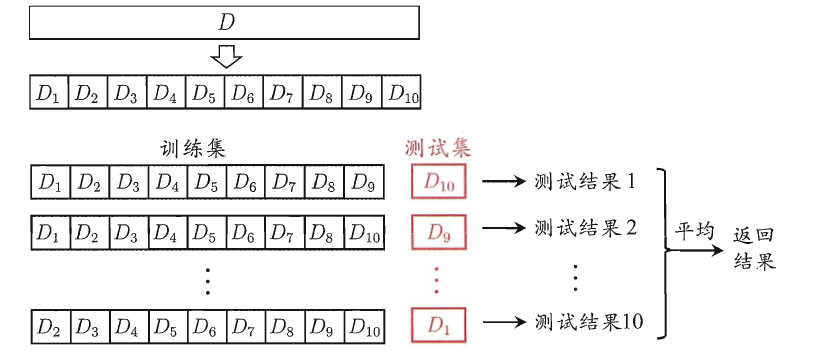
上图会生成10个模型，那现实中，怎么使用交叉验证呢？

k的经验值（西瓜书）：

• 10 最常用
• 5.20等也常用

作用：

1. 用于调节超参数
   不同的超参数分别做一次K折交叉验证，简单情况下，取mean最小的那组超参。但实际上，还会考虑error的方差，一般折中，选择mean和方差都较小的。下面的例子我们用iris数据和KNN模型

from sklearn.cross_validation import cross_val_score

knn = KNeighborsClassifier(n_neighbors=5)
# 这里的cross_val_score将交叉验证的整个过程连接起来，不用再进行手动的分割数据
# cv参数用于规定将原始数据分成多少份
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
print scores
[ 1.          0.93333333  1.          1.          0.86666667  0.93333333
  0.93333333  1.          1.          1.        ]

# use average accuracy as an estimate of out-of-sample accuracy
# 对十次迭代计算平均的测试准确率
print scores.mean()
0.966666666667

# search for an optimal value of K for KNN model
k_range = range(1,31)
k_scores = []
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
    k_scores.append(scores.mean())

print k_scores
[0.95999999999999996, 0.95333333333333337, 0.96666666666666656, 0.96666666666666656, 0.96666666666666679, 0.96666666666666679, 0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 0.98000000000000009, 0.97333333333333338, 0.97333333333333338, 0.97333333333333338, 0.97333333333333338, 0.98000000000000009, 0.97333333333333338, 0.98000000000000009, 0.96666666666666656, 0.96666666666666656, 0.97333333333333338, 0.95999999999999996, 0.96666666666666656, 0.95999999999999996, 0.96666666666666656, 0.95333333333333337, 0.95333333333333337, 0.95333333333333337]

import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(k_range, k_scores)
plt.xlabel("Value of K for KNN")
plt.ylabel("Cross validated accuracy")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

2. 用于模型选择
   用模型A做一次 K折交叉验证，再用模型B做一次，看哪个模型好（error小），选哪个。通常，自动化参数选择时，可利用RandomizeSearchCV与GridSearchCV两种调参方式进行参数的选择。往往通过随机搜索确定大方向，使用网格化搜索进行精细化搜索。
   关于这两种方法的使用参考【GridSearchCV 与 RandomizedSearchCV 调参】
   和【sklearn非线性回归】网格搜索GridSearchCV和随机搜索RandomizedSearchCV
   【英语好的点官方教程，示例的import 后面可以跳对象详情】

# 10-fold cross-validation with the best KNN model
knn = KNeighborsClassifier(n_neighbors=20)
print cross_val_score(knn, X, y, cv=10, scoring='accuracy').mean()
0.98

# 10-fold cross-validation with logistic regression
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
print cross_val_score(logreg, X, y, cv=10, scoring='accuracy').mean()
0.953333333333
1
2
3
4
5
6
7
8
9
10

3. 用于特征选择
   选特征a,b 做一次 K折交叉验证，再选特征a,b,c做一次k折交叉验证，然后看看哪个效果好。

# read in the advertising dataset
data = pd.read_csv('http://www-bcf.usc.edu/~gareth/ISL/Advertising.csv', index_col=0)
# create a Python list of three feature names
feature_cols = ['TV', 'Radio', 'Newspaper']
# use the list to select a subset of the DataFrame (X)
X = data[feature_cols]

# select the Sales column as the response (y)
y = data.Sales
In [18]:
# 10-fold cv with all features
lm = LinearRegression()
scores = cross_val_score(lm, X, y, cv=10, scoring='mean_squared_error')
print scores
[-3.56038438 -3.29767522 -2.08943356 -2.82474283 -1.3027754  -1.74163618
 -8.17338214 -2.11409746 -3.04273109 -2.45281793]
 
# fix the sign of MSE scores
mse_scores = -scores

# convert from MSE to RMSE
rmse_scores = np.sqrt(mse_scores)
# calculate the average RMSE
print rmse_scores.mean()
1.69135317081

# 10-fold cross-validation with two features (excluding Newspaper)
feature_cols = ['TV', 'Radio']
X = data[feature_cols]
print np.sqrt(-cross_val_score(lm, X, y, cv=10, scoring='mean_squared_error')).mean()
1.67967484191
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

关于scores产生负值

可换评估方法scoring为’neg_mean_squared_error’，可查看:

• scoring官方指导，其中没有"mean_squared_error"，因为"mean_squared_error is deprecated"。现在要用neg_mean_squared_error且 neg_mean_squared_error=-1 * mean_squared_error
• cross_val_score 官方指导
• 各种scoring数学解释

3.3 留一法 leave-one-out cross validation

留一法是k折交叉验证k=m（m为样本数）时候的特殊情况。即每次只留下一个样本做测试集，其它样本做训练集，需要训练k次，测试k次。留一法计算最繁琐，但样本利用率最高。因为计算开销较大，所以适合于小样本的情况。

• 优点：样本利用率高。
• 缺点：计算繁琐。

3.4 自助法bootstrapping

自助法以自助采样为基础（有放回采样）。每次随机从D中挑选一个样本，放入$D^{\prime }$ 中，然后将样本放回D中，重复m次之后，得到了包含m样本的数据集$D^{\prime }$。

训练集：$D^{\prime }$
测试集 ：$D\setminus D^{\prime }$ （$\setminus 表示集合减法$）

样本在m次采样中始终不被采到的概率是$(1-\frac{1}{m}{)}^m$，取极限$\underset{m\to \infty }{\lim }(1-\frac{1}{m}{)}^m=\frac{1}{e}=0.368$。即$D$中约有36.8%的样本未出现在$D^{\prime }$中。这样，仍然使用m个训练样本，但约有1/3未出现在训练集中的样本被用作测试集。

• 优点：自助法在数据集较小、难以有效划分训练/测试集时很有用。
• 缺点：然而自助法改变了初始数据集的分布，这回引入估计偏差。

参考：
https://www.cnblogs.com/hider/p/15781829.html
https://zhuanlan.zhihu.com/p/35394638
https://zhuanlan.zhihu.com/p/48976706
https://blog.csdn.net/pxhdky/article/details/85206705
https://blog.csdn.net/JasonDing1354/article/details/50562513