一、买卖股票的最好时机(二)

解法一:动态规划(推荐)

• 用dp[i][0]表示第i天不持股到该天为止的最大收益，dp[i][1]表示第i天持股，到该天为止的最大收益。
• 第一天不持股，则总收益为0，dp[0][0]=0；第一天持股，则总收益为买股票的花费，此时为负数，dp[0][1]=−prices[0]。
• 对于之后的每一天，如果当天不持股，有可能是前面的若干天中卖掉了或是还没买，因此到此为止的总收益和前一天相同，也有可能是当天卖掉股票，我们选择较大的状态dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])；
• 如果当天持股，可能是前几天买入的还没卖，因此收益与前一天相同，也有可能是当天买入，减去买入的花费，同样是选取最大值：dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        //dp[i][0]表示某一天不持股到该天为止的最大收益，dp[i][1]表示某天持股，到该天为止的最大收益
        vector<vector<int> > dp(n, vector<int>(2, 0)); 
        //第一天不持股，总收益为0
        dp[0][0] = 0; 
        //第一天持股，总收益为减去该天的股价
        dp[0][1] = -prices[0]; 
        //遍历后续每天，状态转移
        for(int i = 1; i < n; i++){ 
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        //最后一天不持股，到该天为止的最大收益
        return dp[n - 1][0]; 
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

时间复杂度：O(n)，其中n为数组长度，遍历一次数组
空间复杂度：O(n))，动态规划辅助数组相当于两个一维数组

解法二:贪心

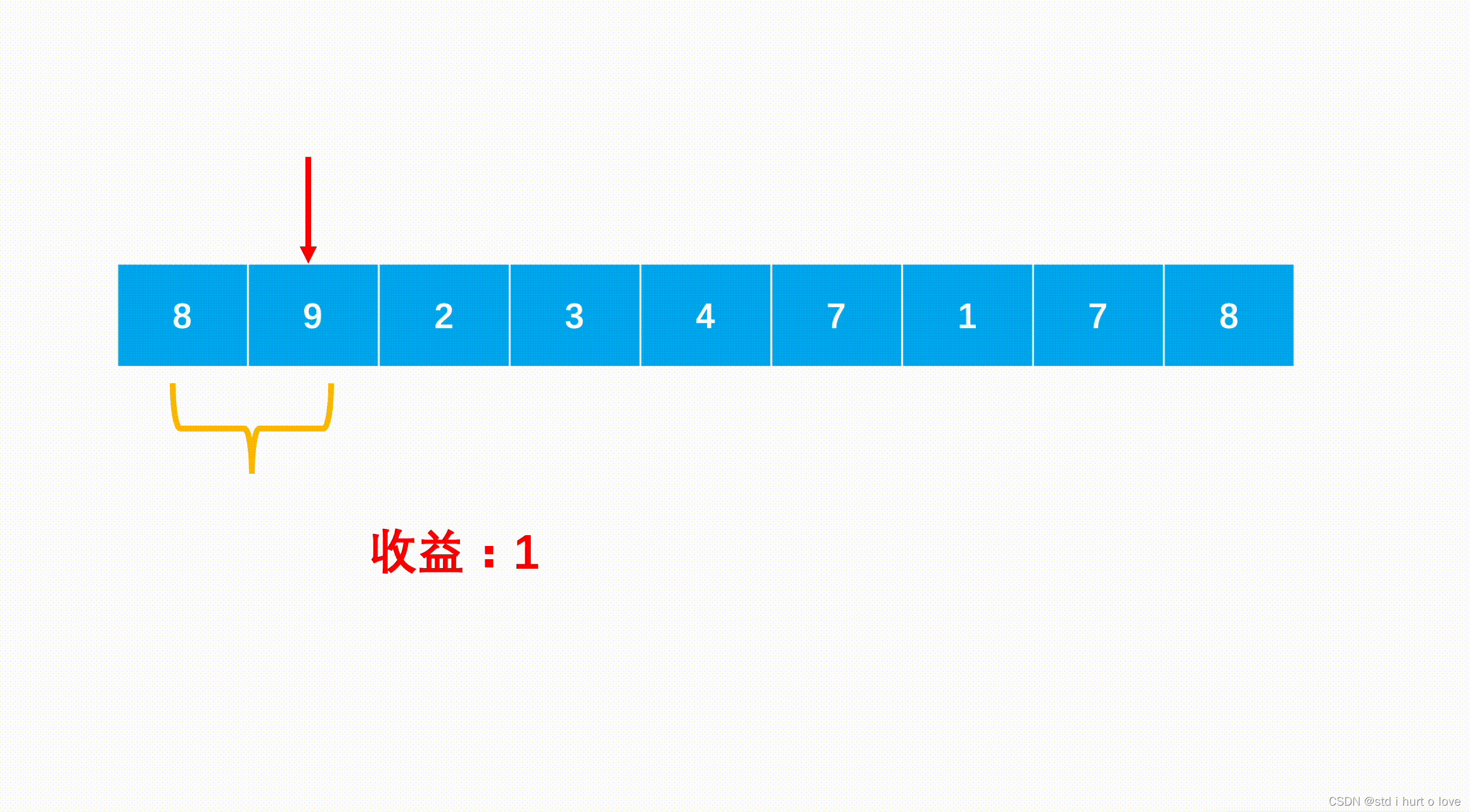
其实我们要想获取最大收益，只需要在低价买入高价卖出就可以了，因为可以买卖多次。利用贪心思想：只要一段区间内价格是递增的，那么这段区间的差值就是我们可以有的收益。

• 遍历数组，只要数组后一个比前一个更大，就可以有收益。
• 将收益累加，得到最终结果。
  

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for(int i = 1; i < prices.size(); i++){
            //只要某段在递增就有收益
            if(prices[i - 1] < prices[i]) 
                //收益累加
                res += prices[i] - prices[i - 1]; 
        }
        return res;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14

时间复杂度：O(n)，其中n为数组长度，遍历一次数组
空间复杂度：O(1)，常数级变量，没有使用额外辅助空间

二、买卖股票的最好时机(三)

解法:动态规划

这道题与买卖股票的最好时机(一)的区别在于最多可以买入卖出2次，那实际上相当于它的状态多了几个，对于每天有到此为止的最大收益和持股情况两个状态，持股情况有了5种变化，我们用：

dp[i][0]表示到第i天为止没有买过股票的最大收益
dp[i][1]表示到第i天为止买过一次股票还没有卖出的最大收益
dp[i][2]表示到第i天为止买过一次也卖出过一次股票的最大收益
dp[i][3]表示到第i天为止买过两次只卖出过一次股票的最大收益
dp[i][4]表示到第i天为止买过两次同时也买出过两次股票的最大收益
于是使用动态规划，有了如下的状态转移

• 与上述提到的题类似，第0天有买入了和没有买两种状态：dp[0][0]=0、dp[0][1]=−prices[0]
• 对于后续的每一天，如果当天还是状态0，则与前一天相同，没有区别；
• 如果当天状态为1，可能是之前买过了或者当天才第一次买入，选取较大值：dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])；
• 如果当天状态是2，那必须是在1的状态下（已经买入了一次）当天卖出第一次，或者早在之前就卖出只是还没买入第二次，选取较大值：dp[i][2]=max(dp[i−1][2],dp[i−1][1]+prices[i])；
• 如果当天状态是3，那必须是在2的状态下（已经卖出了第一次）当天买入了第二次，或者早在之前就买入了第二次，只是还没卖出，选取较大值：dp[i][3]=max(dp[i−1][3],dp[i−1][2]−prices[i]);
• 如果当天是状态4，那必须是在3的状态下（已经买入了第二次）当天再卖出第二次，或者早在之前就卖出了第二次，选取较大值：dp[i][4]=max(dp[i−1][4],dp[i−1][3]+prices[i])。
• 最后我们还要从0、第一次卖出、第二次卖出中选取最大值，因为有可能没有收益，也有可能只交易一次收益最大。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        //初始化dp为最小
        vector<vector<int> > dp(n, vector<int>(5, -10000)); 
        //第0天不持有状态
        dp[0][0] = 0; 
        //第0天持有股票
        dp[0][1] = -prices[0]; 
        //状态转移
        for(int i = 1; i < n; i++){ 
            dp[i][0] = dp[i - 1][0]; 
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        //选取最大值，可以只操作一次
        return max(dp[n - 1][2], max(0, dp[n - 1][4])); 
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

时间复杂度：O(n)，其中n为数组长度，只遍历一次数组
空间复杂度：O(n)，动态规划二维辅助相当于5个一维数组