-
Chapter8 支持向量机
1 理解支持向量机SVM的原理和目标(what)
1.1 原理
SVM的基本原理时在特征空间中寻找间隔最大化的分离超平面的线性分类器。
- 当训练样本线性可分,通过硬间隔最大化,学习一个线性分类器,即线性可分支持向量机。
- 当训练数据近似线性可分,可引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机。
- 当训练数据线性不可分,通过核函数以及软间隔最大化,学习分线性支持向量机。
1.2 目标
找出所有样本距离无数条线性函数f(x,w,b)最小的距离,再中这些距离中找出最大距离所在的那条直线,即求取w,b的值
如图所示:
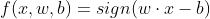 ,其中
,其中 代表向量。
代表向量。样本距离该函数之间的距离为:

所以目标为:


2 掌握支持向量机的计算过程和算法步骤(how)
2.1 计算过程
假设给定一个特征空间上的训练数据集
 ,其中
,其中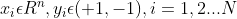 ;
;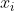 表示为第i个实例(若n大于1,则
表示为第i个实例(若n大于1,则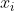 为向量);
为向量);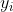 为
为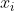 的类标记,即当
的类标记,即当 时,
时,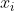 为正例,当
为正例,当 时
时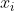 为负例。
为负例。 称为样本点。
称为样本点。给定线性可分训练数据集,通过间隔最大化得到的分离超平面为
 ,相应的分类决策函数
,相应的分类决策函数 ,该决策函数称为线性可分支持向量机。
,该决策函数称为线性可分支持向量机。 是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度。
是某个确定的特征空间转换函数,它的作用是将x映射到(最高的)维度。求解分离超平面问题=求解相应的凸二次规划问题。
(1)根据题设
 ,有当
,有当 ,
,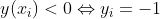
从而
 。【
。【 为预测值
为预测值 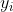 为真实值】
为真实值】按一定的比例改变w,b(此时超平面的位置不会改变,但可以使得函数间隔改变),则t*y的值同样改变,从而:
 ,其中
,其中 为
为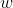 的
的 范数。
范数。目标函数:
![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](https://1000bd.com/contentImg/2022/08/02/071151757.gif)
(2)(假如几何距离为B,即
 (B为常数)
(B为常数)
等式两边除以B:
 ,此时几何距离变成了1。
,此时几何距离变成了1。
通过等比例缩放w的方法,使得这两类点的函数值都满足
 ,即约束条件。
,即约束条件。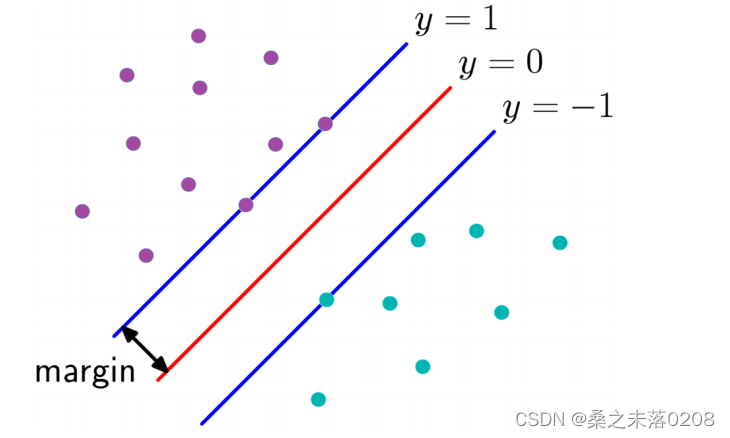
(3)因此原问题可以转化为以下问题:
约束条件——

原目标函数——
![\underset{w,b}{argmax}\left \{ \frac{1}{||w||}\underset{i}{min} [y_{i}\cdot (w^{T}\cdot \Phi (x_{i})+b)]\right \}](https://1000bd.com/contentImg/2022/08/02/071151757.gif)
新目标函数——
 ,即
,即 ,即
,即
(4)所用方法:拉格朗日乘子法
设函数

原问题是极小极大问题:

原问题的对偶问题是极大极小问题:
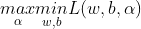
然后分别对
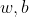 求偏导,令其为0:
求偏导,令其为0: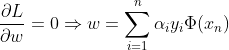


即在
 约束条件下求解:
约束条件下求解: 
添加负号变为求解:


2.2 举例说明

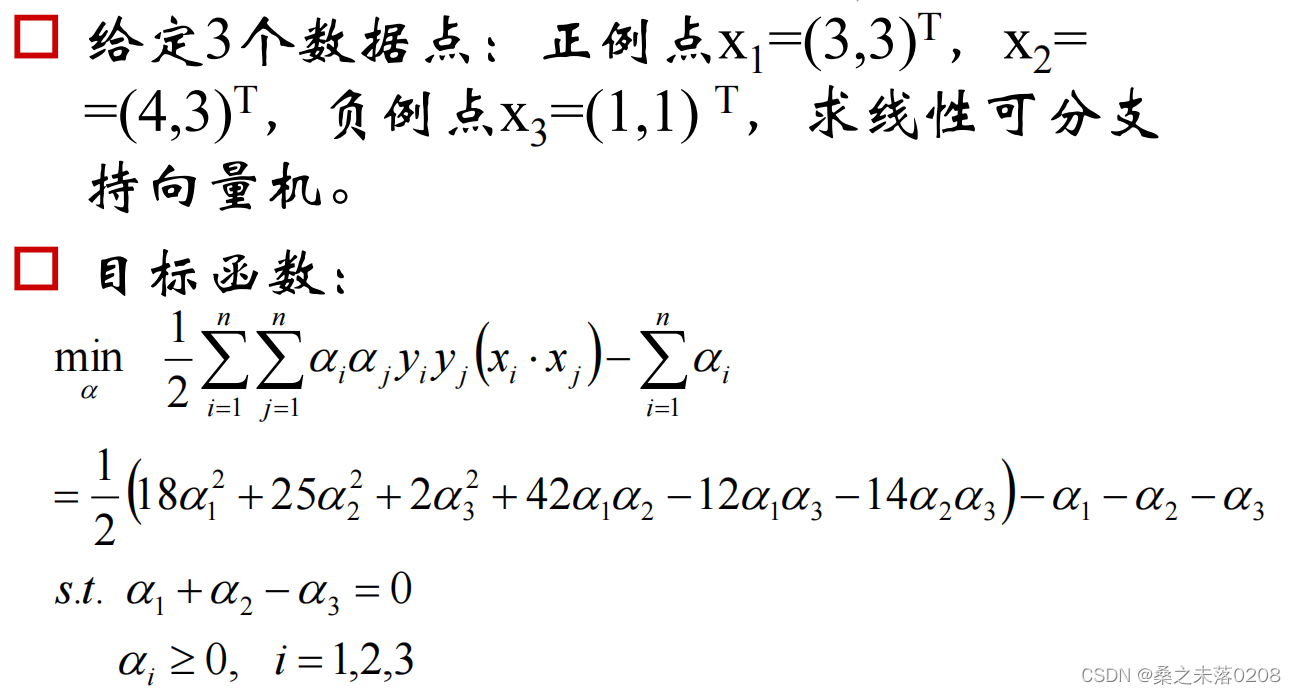

 我们可以看到
我们可以看到 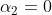 ,则
,则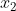 为非支持向量。
为非支持向量。2.3 拉格朗日乘子法
约束条件:
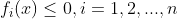 ,
,
目标:

构造函数:
 ,其中
,其中 任意值。
任意值。所以
 (原始问题)
(原始问题)对偶函数为
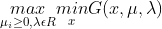
所以接下来对
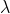 求导,使其为0。
求导,使其为0。3 理解软间隔最大化的含义
当训练数据近似线性可分,可增加松弛变量
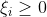 ,通过软间隔最大化,使得汉化间隔加上松弛变量大于等于1,这样约束条件就变成了
,通过软间隔最大化,使得汉化间隔加上松弛变量大于等于1,这样约束条件就变成了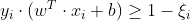 ,而目标函数就变为
,而目标函数就变为
C小则过渡带越宽,所以有泛化能力。C大时,为了目标函数最小,实际上需要使得
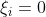 ,即变成线性可分。
,即变成线性可分。所以:带松弛因子的SVM拉格朗日函数如下:




ps:实际上损失函数为

4 核函数
4.1 定义
可以使用核函数,将原始输入空间映射到新的特征空间,从而,使得原本线性不可分的样本可能在核空间可分。
多项式核函数:

高斯核RBF函数:
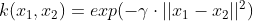
Sigmoid核函数:

在实际应用中,往往依赖先验领域知识/交叉验证等方案才能选择有效的核函数。
没有更多先验信息,则使用高斯核函数。
4.2 多项式核
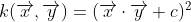
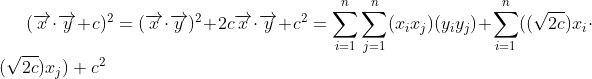

例如:当n=3时,



5 总结
(1)SVM可以用来划分多类别:若有1,2,3,4类,可以通过
1 vs rest:1——234,2——134,3——124,4——123
1 vs 1:1——2,1——3,1——4,2——3,2——4,4——4
(2)SVM和Logistic回归的比较
SVM:直接输出类别,不给出后验概率;
Logistic回归:会给出属于哪个类别的后验概率。
重点:两者目标函数的异同。
-
相关阅读:
基于extended resource扩展节点资源
软件测试正在面试银行的可以看下这些面试题
Python 安装js环境
Ajax--》请求操作以及跨域相关讲解
2022中国国际防伪溯源技术展览会 | 防伪溯源 | 智慧包装 | 安全印刷
JavaScript小技能:事件
网络安全与基础设施安全局(CISA):两国将在网络安全方面扩大合作
Hive的时间操作函数
【2024秋招】2023-9-16 贝壳后端开发二面
55.跳跃游戏
- 原文地址:https://blog.csdn.net/qwertyuiop0208/article/details/126050379