-
矩阵分析与应用-14-行列式
行列式
一个
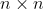 正方矩阵
正方矩阵 的行列式记作
的行列式记作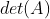 或
或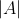 ,定义为
,定义为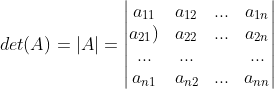
若
 ,则它的行列式由
,则它的行列式由 给出。
给出。矩阵
 去掉第i行和第j列之后得到的剩余行列式记作
去掉第i行和第j列之后得到的剩余行列式记作 ,称为元素
,称为元素 的余子式。特别地,当
的余子式。特别地,当 主时,
主时,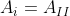 称为
称为 的主子式。若令
的主子式。若令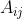 是
是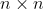 矩阵
矩阵 删去第i行和第j列之后得到的(n - 1)×(n -1)子矩阵,则
删去第i行和第j列之后得到的(n - 1)×(n -1)子矩阵,则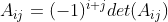
一个
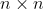 矩阵的行列式等于其任意行(或列)的元素与相对应的余子式乘积之和,
矩阵的行列式等于其任意行(或列)的元素与相对应的余子式乘积之和,也就是:
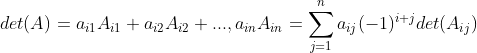
和
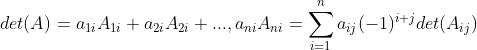
行列式不等于零的矩阵称为非奇异短阵。
非奇异矩阵
 存在逆知阵
存在逆知阵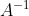 。
。关于行列式的等式关系
行列式服从以下等式关系。
(1)〕如果矩阵的两行(或列)互换位置,则行列式保持不变。
(2)若矩阵的某行(或列)是其他行(或列)的线性组合,则det(A)=0。特别地,若某行(或列)与另一行(或列)成正比或相等,或者某行(或列)的元素均等于零,则det(A) = 0。
(3)任何一个正方矩阵A和它的转置矩阵AT具有相同的行列式,即
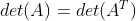
![det(A^H)=[det(A^T)]^*](https://1000bd.com/contentImg/2022/08/02/065339569.gif)
(4)单位矩阵的行列式等于1,即
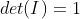 。
。(5)一个Hernitian矩阵的行列式为实数,因为
![det(A)=det(A^H)=det(A^T)\Rightarrow det(A)=det(A^*)=[det(A)]^*](https://1000bd.com/contentImg/2022/08/02/065341700.gif)
(6)两个矩阵乘积的行列式等于它们的行列式的乘积,即
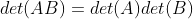
(7)对于一个三角(上三角或下三角)矩阵A,其行列式等丁三角矩阵主对角线所有元素的乘积,即
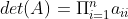
一个对角矩阵
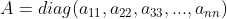 的行列式也等丁其对角元素的乘积。
的行列式也等丁其对角元素的乘积。(8)给定一个任意的常数(可以是复数) c,则
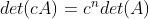
(9)若A非奇异,则
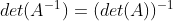 。
。(10)对于矩阵
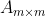 ,
, 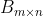 ,
,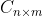 ,
,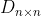 ·分块矩阵的行列式满足
·分块矩阵的行列式满足 非奇异
非奇异
D非奇异
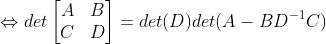
关于行列式的不等式关系
(1) Cauchy-Schwartz不等式:若A,B都是mx n矩阵,则
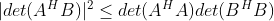
(2) Hadamard不等式;对于n × m矩阵A,有
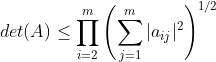
(3)Fischer不等式:若
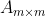 ,
,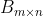 ,
,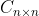 ,则
,则 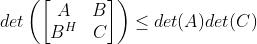
(4) Minkowski不等式:若
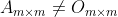 ,
,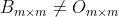 半正定,则
半正定,则![\sqrt[m]{det(A+B)}\geq \sqrt[m]{det(A)}+\sqrt[m]{det(B)}](https://1000bd.com/contentImg/2022/08/02/065359780.gif)
(5)正定矩阵A的行列式大于0,即det(A) >0。
(6)半正定矩阵A的行列式大于或者等于0,即det(A) ≥0。
(7)若mx m矩阵A半正定,则
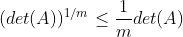
(8)若矩阵
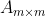 ,
,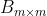 均半正定,则
均半正定,则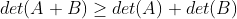
(9)若
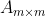 正定,
正定,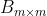 半正定,则
半正定,则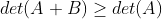
(10)若
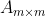 正定,
正定,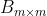 半负定,则
半负定,则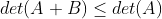
-
相关阅读:
交互与前端16 Tabulator 表格实践4
【若依vue框架学习】2.JWT的token/权限认证
【第39篇】RepLKNet将内核扩展到 31x31:重新审视 CNN 中的大型内核设计
CMake教程——Leeds_Garden
怎么用vscode创建工程
java基于Springboot+Vue的高校生活服务平台 element 前后端分离
《算法之美》读后感
sql server笔记1(表的定义)
Python函数详解(二)——函数的参数传递基础
【Python】八、函数的使用
- 原文地址:https://blog.csdn.net/Xiao__fly/article/details/126064472