python：Möller–Trumbore射线三角面相交算法

Möller–Trumbore射线三角面相交算法（The Möller–Trumbore ray-triangle intersection algorithm) 是一种计算机图形学中经典的算法，用来计算射线和三维空间中三角形的交点。该方法的优点是方法速度快，存储空间少。

输入输出

输入： 给定3维空间中的三个点构成一个三角面片，再给定一个射线起点和方向向量；
输出： 求射线和三角平面在三维空间中的交点。

---

结果展示

输入： 三角形点[[0, 0, 1], [0, 1, 0], [1, 0, 0]]
方向[2,2,2]
输出： 蓝色交点（0.333，0.333，0.333）

---

计算权重系数

import numpy as np

import pyvista as pv


def ray_triangle_intersection(ray_start, ray_vec, triangle):
    """Moeller–Trumbore intersection algorithm.

    Parameters
    ----------
    ray_start[n, 3] : np.ndarray
        Length three numpy array representing start of point.

    ray_vec : np.ndarray
        Direction of the ray.

    triangle : np.ndarray
        ``3 x 3`` numpy array containing the three vertices of a
        triangle.

    Returns
    -------
    bool
        ``True`` when there is an intersection.

    tuple
        Length three tuple containing the distance ``t``, and the
        intersection in unit triangle ``u``, ``v`` coordinates.  When
        there is no intersection, these values will be:
        ``[np.nan, np.nan, np.nan]``

    """
    # define a null intersection
    null_inter = np.array([np.nan, np.nan, np.nan])

    # break down triangle into the individual points
    v1, v2, v3 = triangle
    eps = 0.000001

    # compute edges
    edge1 = v2 - v1
    edge2 = v3 - v1
    pvec = np.cross(ray_vec, edge2)
    det = edge1.dot(pvec)

    if abs(det) < eps:  # no intersection
        return False, null_inter
    inv_det = 1.0 / det
    tvec = ray_start - v1
    u = tvec.dot(pvec) * inv_det

    if u < 0.0 or u > 1.0:  # if not intersection
        return False, null_inter

    qvec = np.cross(tvec, edge1)
    v = ray_vec.dot(qvec) * inv_det
    if v < 0.0 or u + v > 1.0:  # if not intersection
        return False, null_inter

    t = edge2.dot(qvec) * inv_det
    if t < eps:
        return False, null_inter

    return True, np.array([t, u, v])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

主函数，计算交点

# Create a basic triangle within pyvista
points = np.array([[0, 0, 1], [0, 1, 0], [1, 0, 0]])
faces = np.array([3, 0, 1, 2])# 三个点，points的0，1，2点
tri = pv.PolyData(points, faces)# faces是空间三角形面，points是三角形顶点

# cast a ray above pointed downwards
start = np.array([0, 0, 0])
direction = np.array([2, 2, 2])

# compute if the intersection exists
inter, tuv = ray_triangle_intersection(start, direction, points)
t, u, v = tuv

print('Intersected', inter)
print('t:', t)
print('u:', u)
print('v:', v)

a, b, c = (1 - u - v), u, v
point = tri.points[0] * a + tri.points[1] * b + tri.points[2] * c

print(point)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

可视化

if inter:

    # reconstruct intersection point in barycentric coordinates.  See
    # https://en.wikipedia.org/wiki/Barycentric_coordinate_system
    a, b, c = (1 - u - v), u, v
    point = tri.points[0] * a + tri.points[1] * b + tri.points[2] * c

    pl = pv.Plotter()
    pl.add_text(f'Intersected at ({point[0]:.3}, {point[0]:.3}, {point[0]:.3})', font_size=26)
    pl.add_mesh(tri)
    _ = pl.add_arrows(
        np.array([start]),
        np.array([direction]),
        show_scalar_bar=False,
        color='r',
        style='wireframe',
    )
    pl.add_points(np.array([point]), point_size=20, render_points_as_spheres=True, color='b')
    pl.add_point_labels(tri, [f'a = {1 - u - v:.3}', f'b = {u:.3}', f'c = {v:.3}'], font_size=40)
    pl.show_bounds()
    pl.camera_position = 'xy'
    pl.show()

else:  # no intersection
    pl = pv.Plotter()
    pl.add_text('No intersection')
    _ = pl.add_arrows(
        np.array([start]),
        np.array([direction]),
        show_scalar_bar=False,
        color='r',
        style='wireframe',
    )
    pl.add_mesh(tri)

    pl.show_bounds()
    pl.camera_position = 'xy'

    pl.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

---

原理

射线的参数： o是射线的起点，D是射线的方向。
如果有一个点从起点o出发，沿着方向D移动任意长度t，到达终点R。如果t不同那么R也不同。通过无数不同的R，我们就能构成整条射线。
如下图所示，射线的起点为P0，沿着方向u前进（红线），P0+tu就构成了整条射线。

通过上述概念，我们可以推广到三角面上，即用两个方向向量|AB|、|AC|和其权重u、v来表示一个空间上的三角形（三个顶点为A，B，C）。

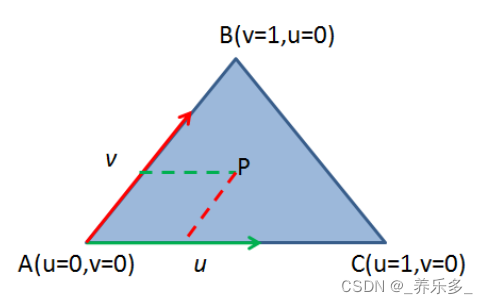
如上图所示，我们给定三角形的参数方程，（1-u-v）V0+uV1+vV2。上图三角形内任意一点都可以由向量和其权重值来表示。比如A点就是在两个方向上移动了0个单位距离。点C在向量|AC|方向移动了1个距离单位。
点P就是沿着AC方向移动了一段距离，又沿着AB移动了一段距离，他们的和向量|AP|就是P点走的方向。
那么三角形内的所有点都由参数u和v控制就可以得到。

于是求解射线和三角形的交点就是求解下面方程的未知数t、u、v，其他都是已知的。

表示为线性方程组：

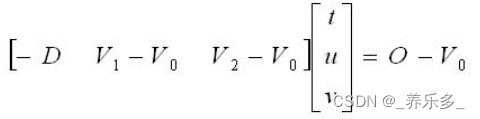
下面解这个方程组，用到两个知识点，一是克莱姆法则，二是向量的混合积。
令E1 = V1 - V0，E2 = V2 - V0，T = O - V0，得

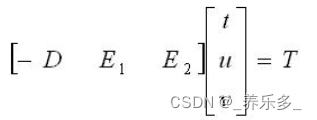
根据克莱姆法则，可得到t,u,v的解

将这三个解联合起来，得

根据混合积公式：

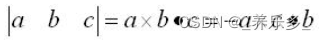
得

令

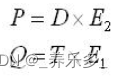
得：

---

代码实现：利用numpy计算和pyvista模块可视化
https://docs.pyvista.org/examples/99-advanced/ray-trace-moeller.html