-
TI mmWave radar sensors Tutorial 笔记 | Module 2: The phase of the IF signal
本系列为TI(Texas Instruments) mmWave radar sensors 系列视频公开课 的学习笔记。
-
视频网址: https://training.ti.com/intro-mmwave-sensing-fmcw-radars-module-1-range-estimation?context=1128486-1139153-1128542
-
关注 下面的公众号,回复“ TI毫米波 ”,即可获取 本系列完整的pdf笔记文件~
内容在CSDN和微信公众号同步更新

- Markdown源文件暂未开源
- 笔记难免存在问题,欢迎联系指正
FMCW Radars – Module 1 : Range Estimation
FMCW Radars – Module 2 : The Phase of the IF Signal
FMCW Radars – Module 3 : Velocity Estimation
FMCW Radars – Module 4 : Some System Design Topics
FMCW Radars – Module 5 : Angle Estimation
Module 2: The Phase of the IF Signal
Last Module: the frequency of IF signal
- f I F = S 2 d / c f_{IF} = S2d/c fIF=S2d/c
This Module:
- look into the phase of the IF signal
- The Phase is very important if we wish to understand the capability of FMCW radar to:
-
respond to very small displacements displacements 位移 in objects
-
measure the velocity very quickly and accurately
- 是heartbeat monitoring and vibration detection的基础
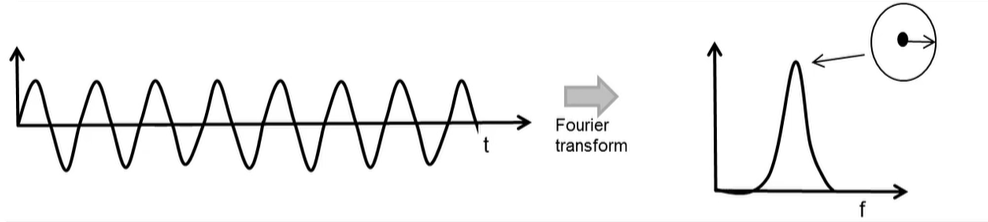
Fourier Transforms: A quick review
- Fourier Transform converts a time domain signal into the frequency domain
- A sinusoid in the time domain produces a peak in the frequency domain
- The signal in the Frequency domian is complex
- each value is a phasor with a amplitude and a phase: A e j θ Ae^{j\theta} Aejθ
- 可用图形表示(如下图)
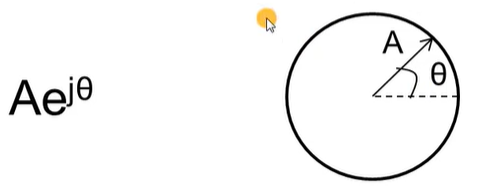
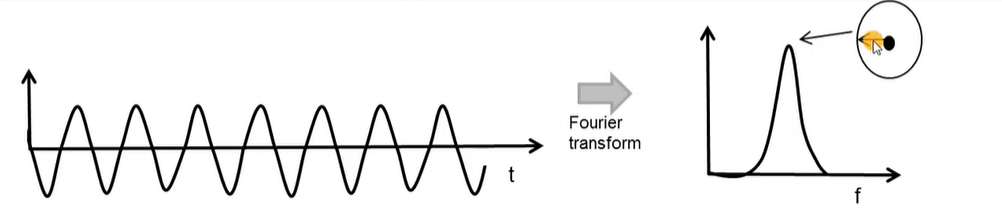
- Phase of the peak is equal to the initial phase of the sinusoid
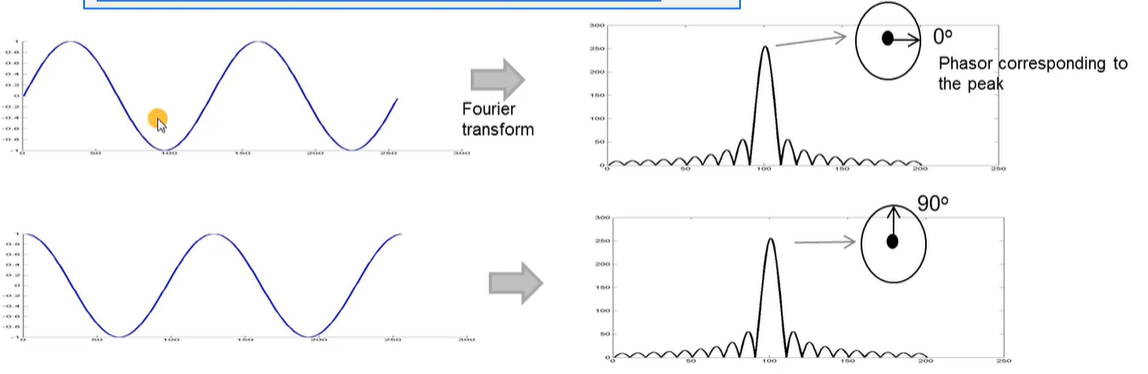
Note: The above is strictly true only for a complex input tone (in the form of e j ω t e^{j\omega t} ejωt)
- 但对于real input概念上也equally applicable with a few mathematical modifications
- 此处为了从概念上进行理解,忽略这些修正
Frequency of the IF signal: Recap from module 1
- 两种观察方式:
- A-t plot
- f-t plot
- In module 1, focus on f-t plot to understand the IF signal
- A single object in front of the radar produces an IF signal with a constant frequency of S 2 d / c S2d/c S2d/c
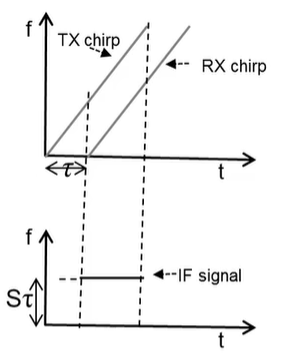
- This module:
- use the A-t plot to analyze the relationship between the Phase and the Distance
Phase of the IF signal
-
Let’s look at the ‘A-t’ plot
- To get more intuition into the nature of the IF signal
-
IF signal:
-
For an object at a distance d from the radar, the IF signal will be a sinusoid:
-
A s i n ( 2 π f t + ϕ 0 ) Asin(2\pi f t + \phi_0) Asin(2πft+ϕ0)
-
其中 f = S 2 d / c f = S2d/c f=S2d/c
-
What is the ϕ 0 \phi_0 ϕ0 :
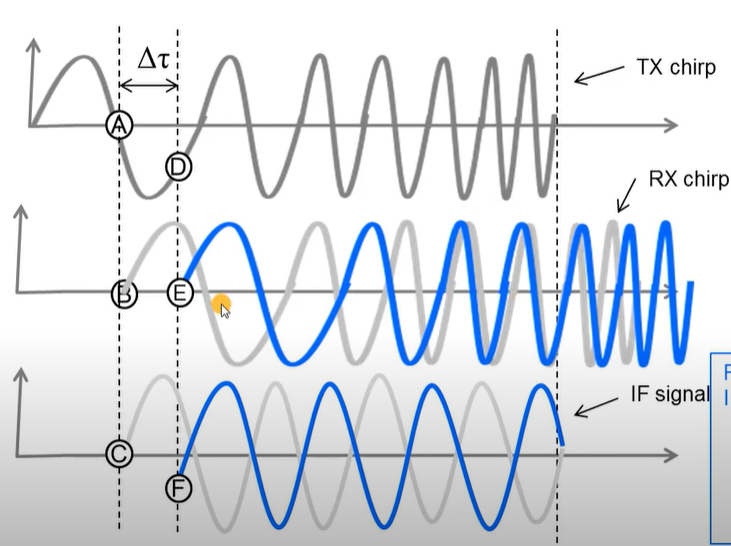
🚩 The phase of point C in the following image C点相位
🚩 Recall: mixer输出信号的initial phase就是 the difference of the initial phase of the two inputs ⇒ \Rightarrow ⇒ 即 (A点相位 - B点相位)
🚩 也是 the peak point in FFT(IF signal) 的相位
-
-
相移 VS 位移 :what happens to the phase fo the IF signal if the object moves by a small ditance Δ τ \Delta \tau Δτ?
-
灰色曲线: before the movement
-
蓝色曲线: after the movement
-
The phase of the TX: delay
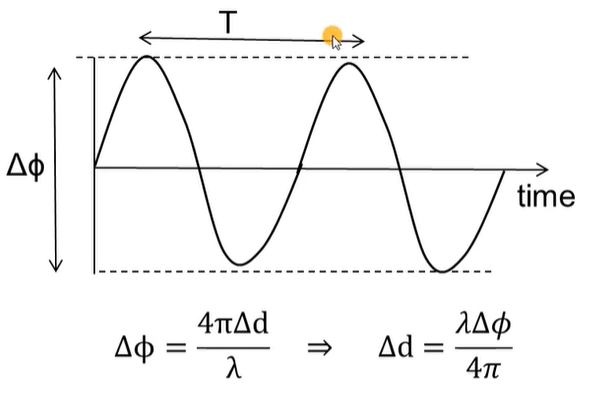
🚩 Phase diference between A and D: Δ Φ = 2 π f c Δ τ = 4 π Δ d λ \Delta \Phi = 2 \pi f_c \Delta \tau = \frac{4\pi \Delta d}{\lambda} ΔΦ=2πfcΔτ=λ4πΔd
-
The phase of the RX: 不变 (注: 因为根据电磁场与波,垂直入射相位改变 π \pi π, 所以不变)
-
Therefore, Δ ϕ \Delta \phi Δϕ of IF signal = Δ ϕ \Delta \phi Δϕ of TX signal = Δ Φ = 2 π f c Δ τ = 4 π Δ d λ =\Delta \Phi = 2 \pi f_c \Delta \tau = \frac{4\pi \Delta d}{\lambda} =ΔΦ=2πfcΔτ=λ4πΔd
-
最终结论: 4 π Δ d λ \frac{4\pi \Delta d}{\lambda} λ4πΔd
-
Sensitivity of the IF signal for small displacements in the object
-
Recall: the IF signal is A s i n ( 2 π f t + ϕ 0 ) Asin(2\pi ft + \phi_0) Asin(2πft+ϕ0)
- f = S 2 d / c f = S2d/c f=S2d/c
- Δ ϕ = 4 π Δ d λ \Delta \phi = \frac{4\pi \Delta d}{\lambda} Δϕ=λ4πΔd
-
Now: 如果目标物体位移了一小段,IF signal的频率和相位将会如何变化?
- 一小段(small): compared to the range resolution of the radar
- An example:
-
S = 50 M H z / u s S = 50MHz/us S=50MHz/us, T c = 40 u s T_c = 40us Tc=40us, 77 G H z 77GHz 77GHz, 1 m m = λ / 4 1mm = \lambda/4 1mm=λ/4
-
What happens if an object in front of the randar changes its position by 1 m m 1mm 1mm
-
Phase: Δ ϕ = 4 π Δ d λ = π = 18 0 ∘ \Delta \phi=\frac{4 \pi \Delta d}{\lambda}=\pi=180^{\circ} Δϕ=λ4πΔd=π=180∘
-
Frequency: by Δ f = S 2 Δ d c = 50 × 1 0 12 × 2 × 1 × 1 0 − 3 3 × 1 0 8 = 333 H z \Delta \mathrm{f}=\frac{\mathrm{S} 2 \Delta d}{c}=\frac{50 \times 10^{12} \times 2 \times 1 \times 10^{-3}}{3 \times 10^{8}}=333 \mathrm{~Hz} Δf=cS2Δd=3×10850×1012×2×1×10−3=333 Hz
🚩 但 尽管 333 Hz looks like a big number ⇒ \Rightarrow ⇒ But in the observation window , this corresponds to only additional Δ f T c = 333 × 40 × 1 0 − 6 = 0.013 \Delta f T_c = 333 \times 40 \times 10^{-6} = 0.013 ΔfTc=333×40×10−6=0.013 cycles
❌ ⇒ \Rightarrow ⇒ 在频谱图中不会被体现
-
结论 : The phase of the IF signal is very sensitive to small changes in object range.
- 如下图所示
- An object at certain distance produces an IF signal with a certain frequency and phase (上图)
- small motion in the object changes the phase of the IF signal but not the frequency
How to measure the velocity (v) of an object using 2 chirps?
- Transmit two chirps separated by T c T_c Tc
- The range-FFTs corresponding to each chirp will have peaks in the same location but with different phase
- The measured phase difference
ω
\omega
ω corresponds to a motion in the object of
v
T
c
vT_c
vTc
- ω = 4 π v T c λ \omega = \frac{4\pi v T_c}{\lambda} ω=λ4πvTc
- ⇒ \Rightarrow ⇒ v = λ ω 4 π T c v=\frac{\lambda \omega}{4 \pi T_c} v=4πTcλω
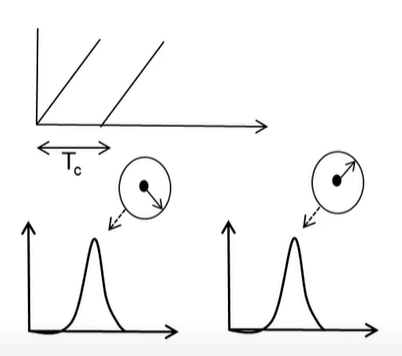
结论 : The phase difference measured across two consecutive chirps can be used to estimate the velocity of the object
Measurements on a Vibrating Object
- blue block:
- Small (amplitude ~1mm) vibrations over time
- Δ d \Delta d Δd is a fraction of a wavelength
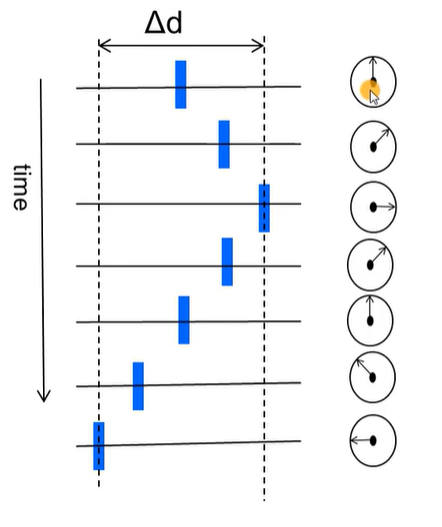
- measure the time evolution of phase
- obtained by FFT
- can be used to estimate both the amplitude and periodicity of the vibration
Epilogue
-
What we learned in this module:
- The phase of IF signal is very sensitve to small changes in the range of the object
- we can exploit it to meaure the velocity
- Δ ϕ = 4 π Δ d λ \Delta \phi = \frac{4\pi \Delta d}{\lambda} Δϕ=λ4πΔd
- v = λ Δ ϕ 4 π T c v=\frac{\lambda \Delta \phi}{4 \pi T_c} v=4πTcλΔϕ
-
下一个目标:
-
How to separate Multiple objects equidistant from the radar, but with differing velocities relative to the radar
🚩 Equi-range objects which have differing velocities relative to the radar can be separated out using a “Doppler-FFT”
✅ see in the next module
-
-
-
相关阅读:
腾讯回应没有获得首批游戏版号,先让小公司回血更要紧;小鹏汽车被曝毁约20余名应届生;大厂一半以上程序员愿意降薪跳槽|极客头条
halcon之区域:多种区域(Region)生成(4)
java Spring Boot pattern.console日志配置中clr支持的颜色
SpringBoot启动原理——SpringApplication《课时十一》
备份与恢复 CR 介绍
MYSQL存储引擎基础知识介绍
三剑客之 awk
基于51单片机的压力监测仪(MPX4115)(Proteus仿真+程序)
dpdk igbuio基础信息
树莓派+超声波模块测距
- 原文地址:https://blog.csdn.net/qazwsxrx/article/details/126056814