-
【算法设计技巧】贪婪算法与回溯算法
贪婪算法
在前面的文章中已经见到了3个贪婪算法(greedy algorithm):Dijkstra 算法、Prim 算法和 Kruskal 算法。贪婪算法分阶段地工作。在每个阶段,可以认为所作决定是好的,而不考虑将来的后果。一般地说,这意味着选择的是某个局部的最优。当算法终止时,我们希望局部最优等于全局最优。如果是这样的话,那么算法就是正确的;否则,算法得到的是一个次最优解。如果不要求绝对最优答案,那么有时候可以用简单的贪婪算法来生成近似的答案,而不是使用一般说来产生准确答案所需要的复杂算法。
调度问题
现有作业 j1,j2,……,jN,已知对应时间分别为t1,t2,……,tN,而处理器只有一个。为把作业平均完成的时间最小化,调度这些作业最好的方式是什么?这里假设非预占调度(nonpreemptive scheduling):一旦开始一个作业,就必须把该作业运行到完成。
举个例子,设有4个作业和相关的运行时间如下所示。
作业 时间 j1 15 j2 8 j3 3 j4 10 一个可能的调度是:j1 用15个单位时间运行结束,j2 用23,j3 用26,而j4 用36个时间单位,所以平均完成时间为 (15+23+26+36)/4 = 25。而另一个更好的调度是按照最短的作业最先进行来安排的,即 j3 用3个单位时间运行结束,j2 用11,j4 用21,j1 用36个时间单位,它产生的平均完成时间为 17.75。
事实上,操作系统调度程序一般把优先权赋予那些更短的作业。
哈夫曼编码
本节将考虑贪婪算法的第二个应用,即文件压缩(file compression)。
字符编码
我们知道,标准的 ASCII 字符集由大约100个“可打印”字符组成,为区分这些字符,需要 ⌈log 100⌉ =7个比特位(二进制位)。即,如果字符集的大小是 C,那么在标准的编码中就需要 ⌈log C⌉ 个比特。
设有一个文件,它只包含字符10个 a,15个 e,12个 i,3个 s,4个 t,再加上13个空格和一个换行符。如图1 所示,这个文件需要174个比特来表示,因为有58个字符而每个字符需要3个比特。
字符 代码 频率 总比特数 a 000 10 30 e 001 15 45 i 010 12 36 s 011 3 9 t 100 4 12 空格 101 13 39 换行符 110 1 3 总计 174 图1 使用一个标准编码方案 提供一种更好的编码以降低所需的总比特数。一种简单的策略可以使典型的大型文件节省 25%,而使许多大型的数据文件节省多达 50% ~ 60%。这种一般的策略就是让代码的长度从字符到字符是变化不等的,同时保证经常出现的字符其代码要短。注意,如果所有的字符都以相同的频率出现,那么节省的问题是不可能存在的。
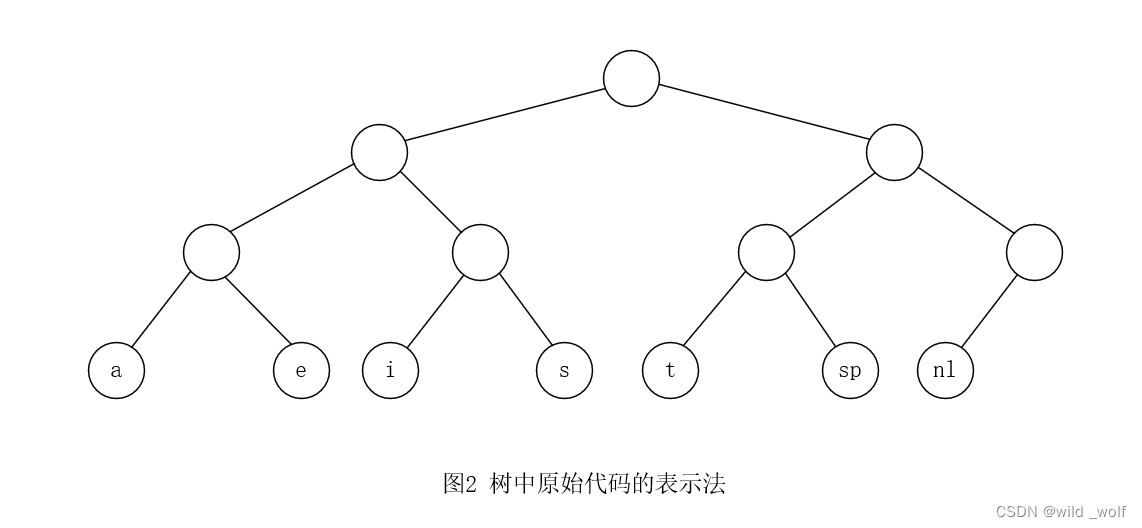
每个字符通过从根节点开始以记录路径的方法表示出来,其中用 0 指示左分支,用 1 指示右分支。在图2 中,s通过从根向左走,然后向右,最后再向右而到达,于是它被编码成011。 如果字符 ci 在深度 di 处并且出现 fi 次,那么该字符代码的值就等于 ∑difi 。
前缀码
这些字符代码的长度是否不同并不重要,只要没有字符代码是别的字符代码的前缀就行,这样一种编码就叫作前缀码(prefix code)。
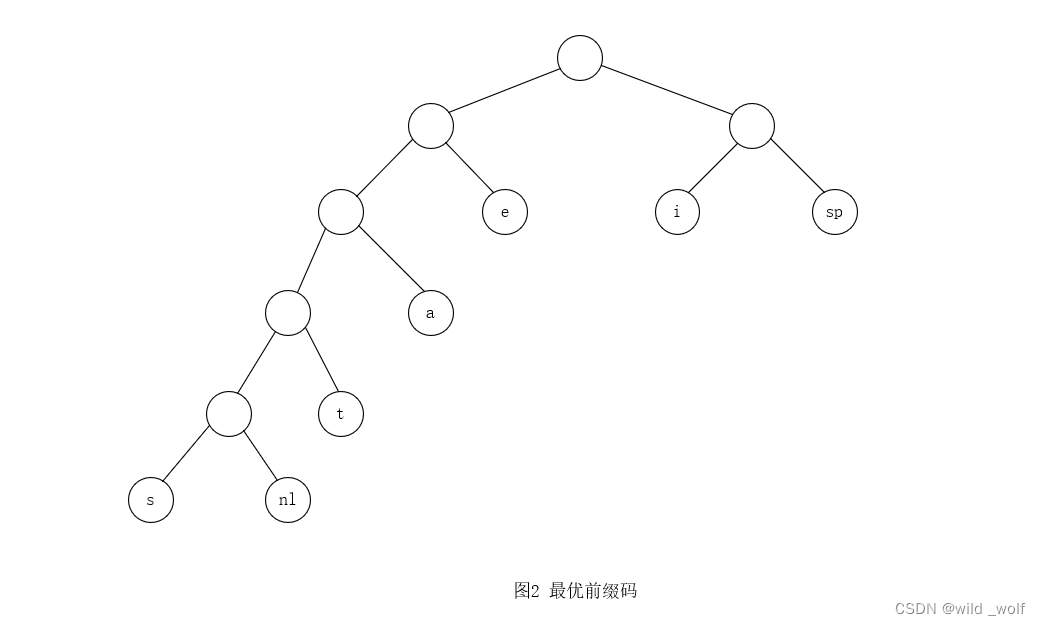
字符 代码 频率 总比特数 a 001 10 30 e 01 15 30 i 10 12 24 s 00000 3 15 t 0001 4 16 空格 11 13 26 换行符 00001 1 5 总计 146 图3 最优前缀码 哈夫曼算法
假设字符个数为 C。哈夫曼算法可以描述为:算法对由树组成的森林进行。一棵树的权等于它的树叶出现的频率的和。任意选取最小权的两棵树 T1 和 T2,并任意形成以 T1 和 T2 为子树的新树,将这样的过程进行 C-1 次。在算法的开始,存在C棵单节点树——每个字符一棵。在算法结束时得到一棵树,这棵树就是最优哈夫曼编码树。
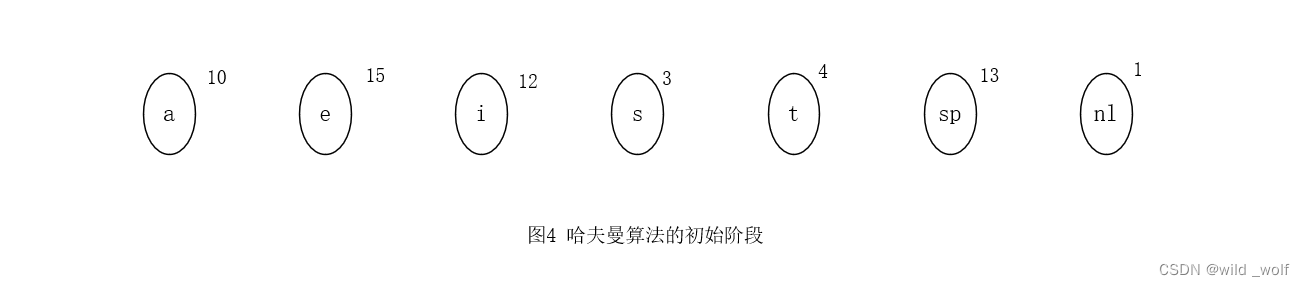
下面通过一个具体的例子来搞清算法的操作。图4 表示的是初始的森林,每棵树的权在根处以小号数字标出。
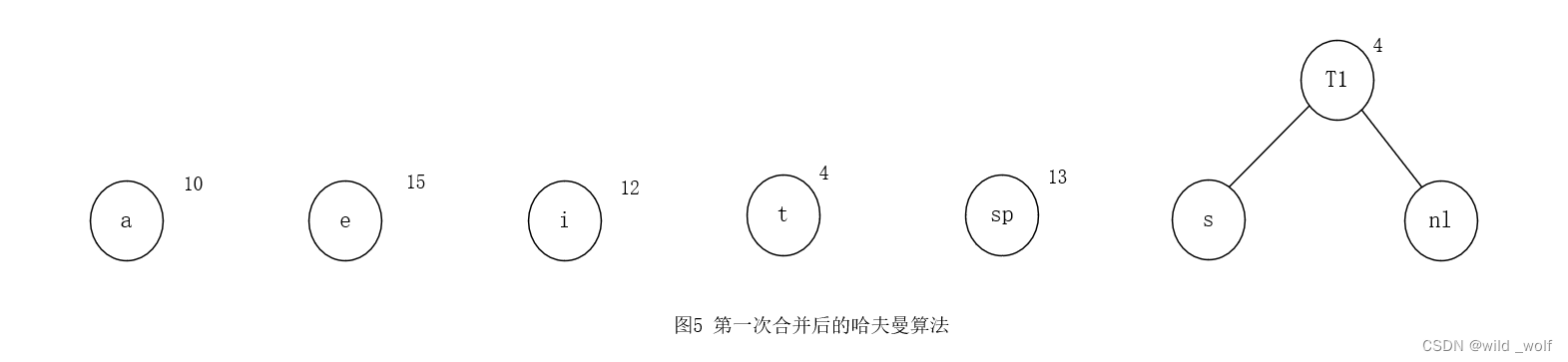
选择两棵权最低的树合并到一起,并将新的根命名为 T1,如图5 所示,这里令s是左儿子(令其为左儿子还是右儿子是任意的)。
现在有六棵树,再任意选取两棵权最小的树。将T1 和 t 合并,树根在 T2,树的权为8,如图6 所示。
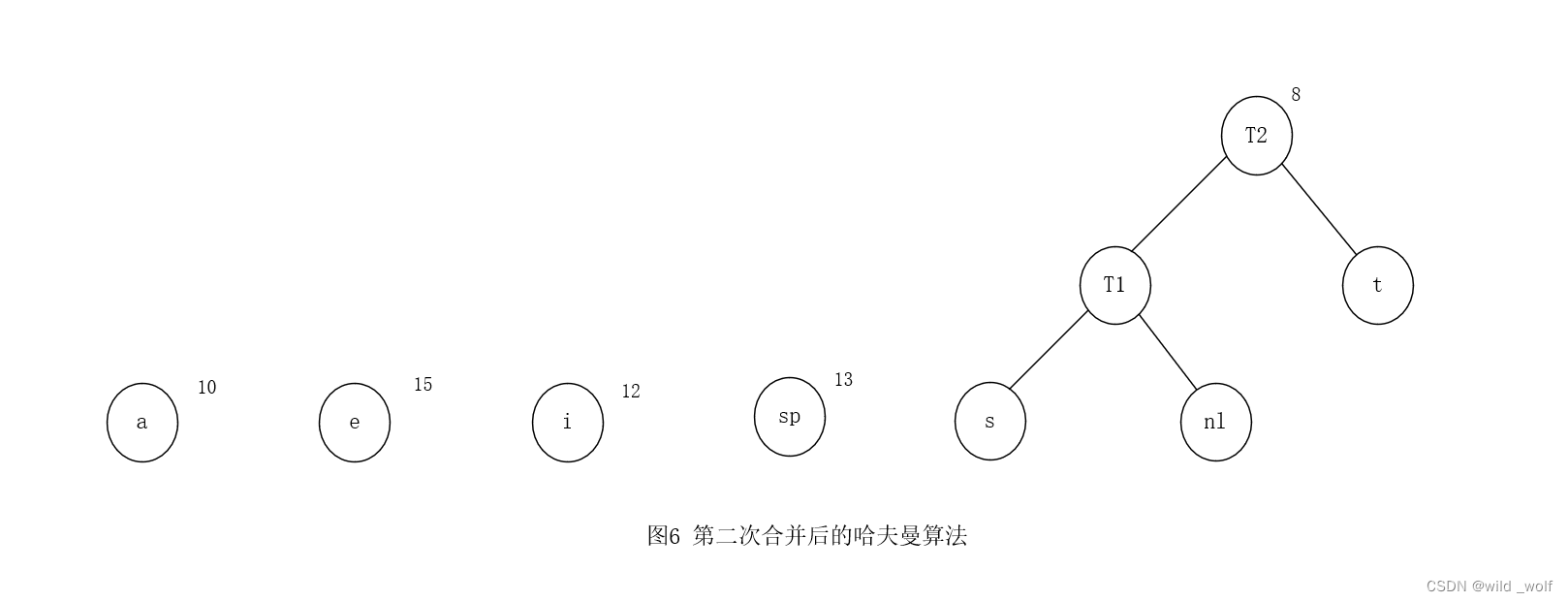
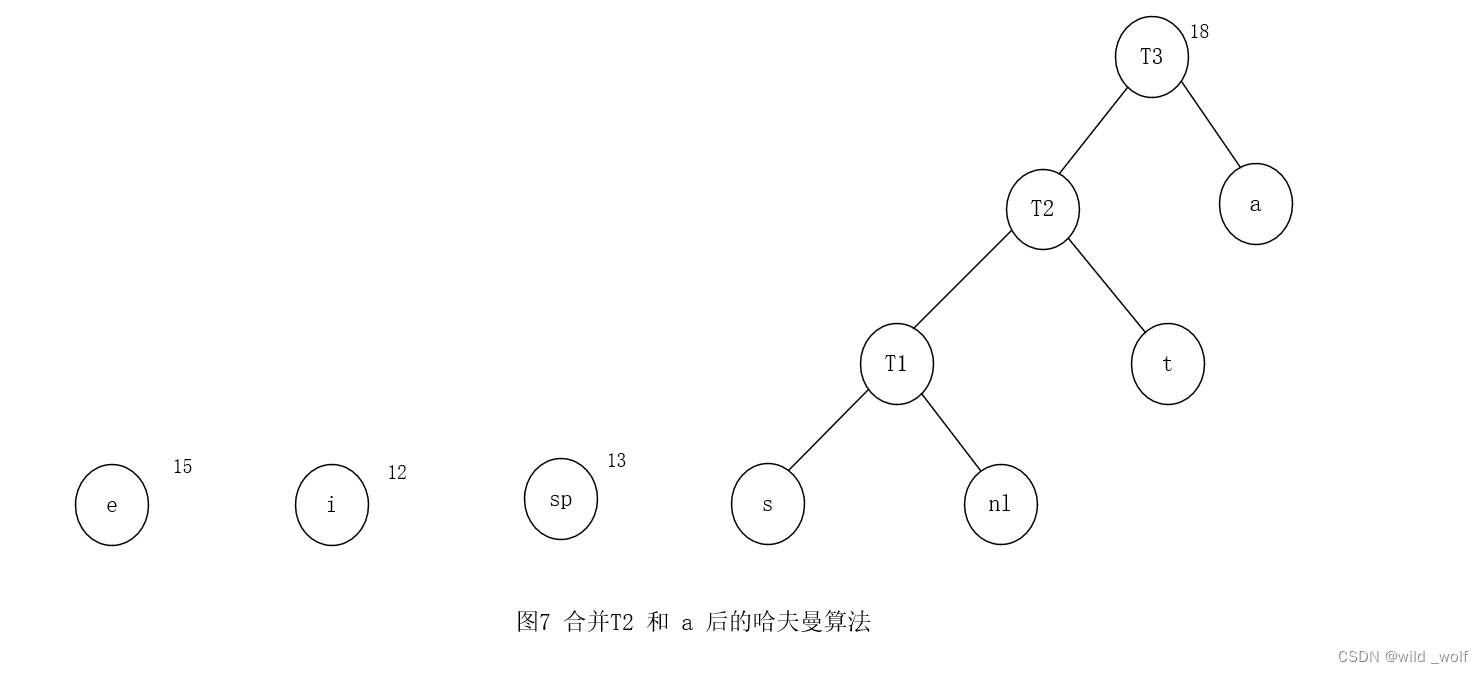
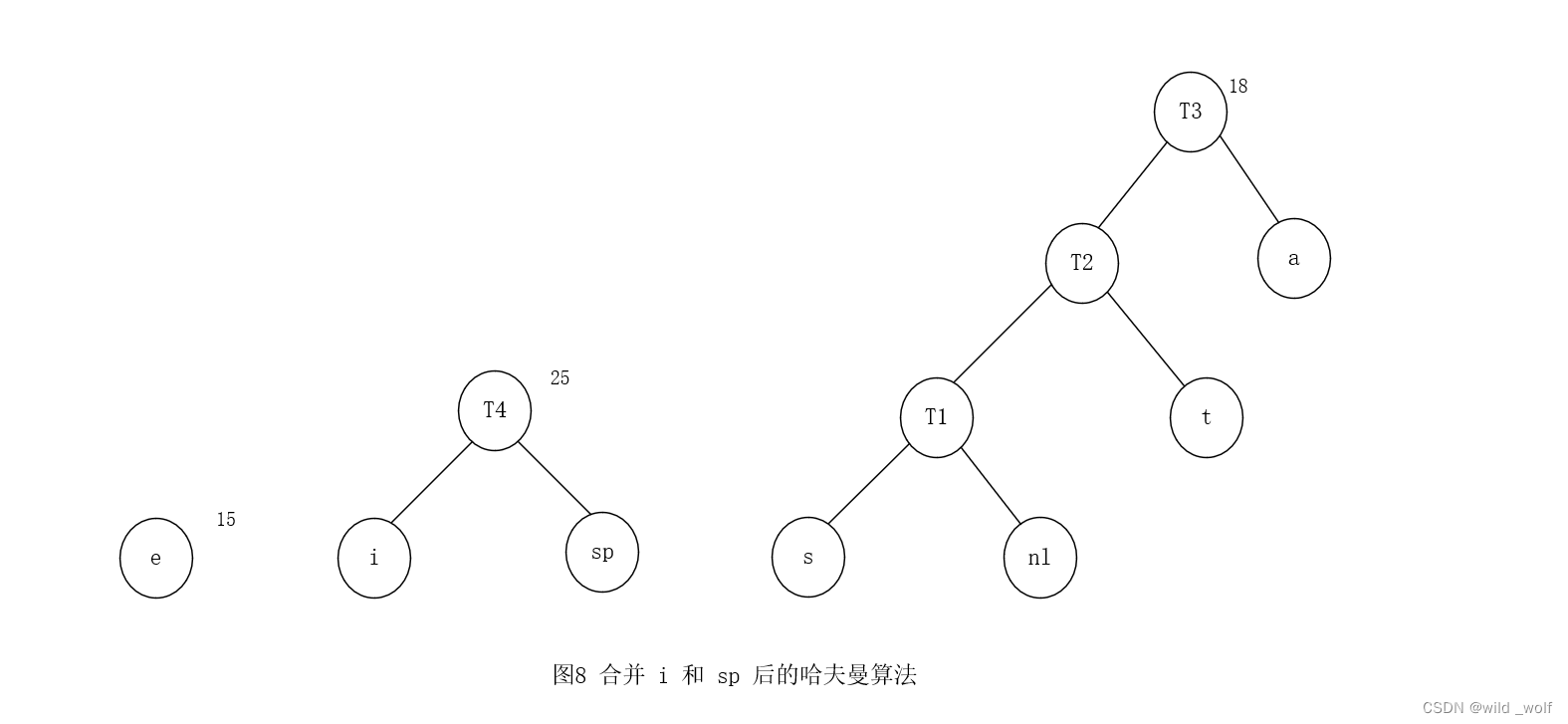
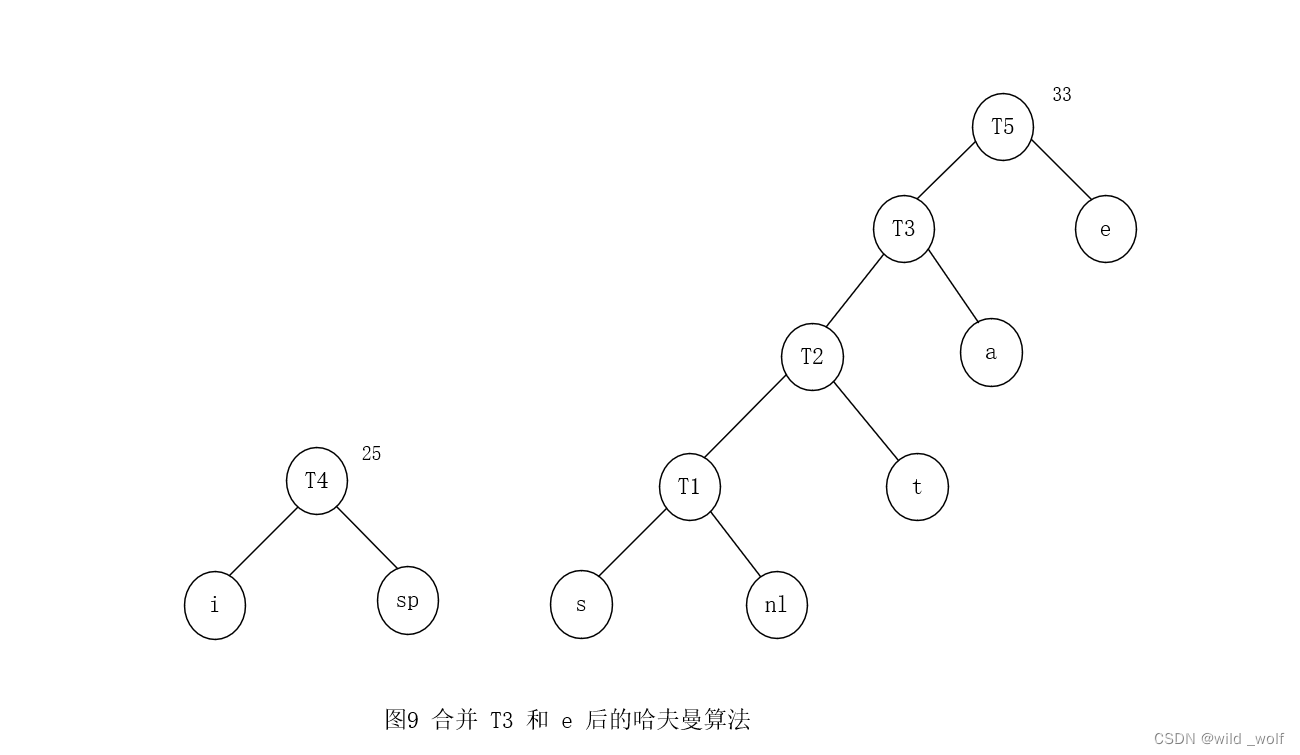
最后,将仅有的两棵剩下的树合并得到图2 所示的最优树,其根在 T6。
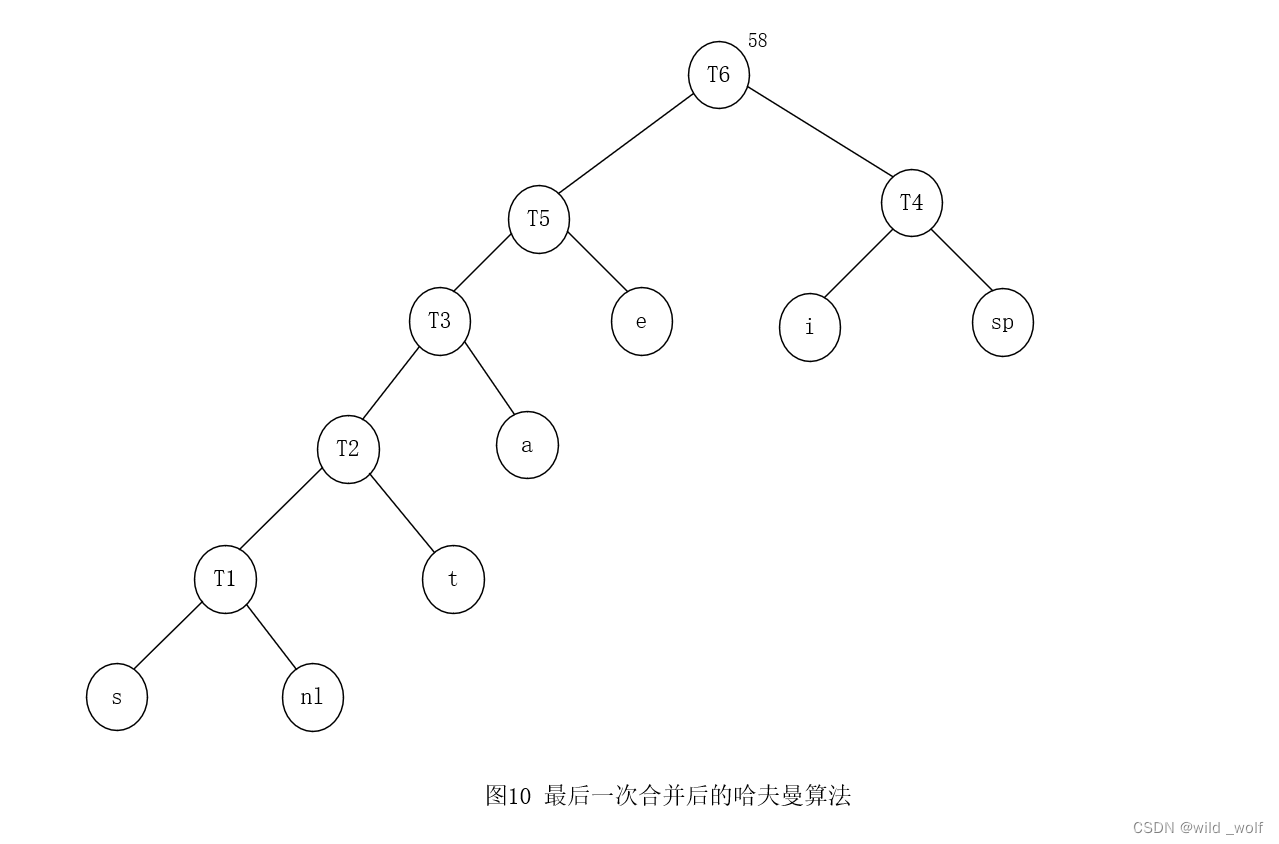
该算法是贪婪算法的原因在于,在每一阶段我们都进行一次合并而没有进行全局的考虑,只是选择两棵最小的树。
近似装箱问题
设给定 N 项物品,大小为s1,s2,……,sN,所有的大小都满足 0< si ≤ 1。问题是要把这些物品装到最小数目的箱子中去,已知每个箱子的容量是1个单位。
有两种类型的装箱问题,第一种是联机装箱问题(online bin packing problem),每一件物品必须放入一个箱子之后才能处理下一件物品。第二种是脱机装箱问题(offline bin packing problem)。在一个脱机算法中,我们做任何事都需要等到所有的输入数据全部读入之后才进行。
联机算法
需考虑的问题:一个联机算法即使在允许无限制计算的情况下是否实际上总能给出最优的解答。我们知道,即使允许无限制的计算,联机算法也必须先放入一项物品然后才能处理下一件物品,并且不能改变决定。
联机算法从不知道输入何时会结束,因此它提供的任何性能保证必须在整个算法的每一瞬时成立。
存在使得任意联机装箱算法至少使用 4/3 最优箱子数的输入。
有3种简单算法保证所用的箱子数不多于2倍的最优装箱数。
下项适合算法
当处理任何一项物品时,我们检查看它是否还能装进刚刚装进物品的同一个箱子中去。如果能装入就将它放入该箱中,否则就开辟一个新的箱子。
首次适合算法
依序扫描这些箱子,并把新的一项物品放入足够盛下它的第一个箱子中。因此,只有当前面那些放置物品的箱子都容不下当前物品时,我们才开辟一个新箱子。
最佳适合算法
该法不是把一项新物品放入所发现的第一个能够容纳它的箱子,而是放到所有箱子中能够容纳它的最满的箱子中。
脱机算法
所有联机算法的主要问题在于将大项物品装箱困难,特别是当它们在输入的后期出现时。围绕这个问题的自然方法是将各项物品排序,把最大的物品放在最先。此时可以应用首次适合算法或最佳适合算法,分别得到首次适合递减算法和最佳适合递减算法。
回溯算法
在许多情况下,回溯算法(backtracking algorithm) 相当于穷举搜索的巧妙实现,但性能一般不理想。然而在某些情形下它相对于蛮力穷举搜索的工作量也是有显著的节省。
在一步内删除一大组可能性的做法叫作裁剪(pruning)。
收费公路重建问题
设给定N个点p1,p2,……,pN,它们位于x轴上,xi 是点 pi 的x坐标。假设x1 =0 ,并假设这些点从左到右给出。
博弈
考虑三连游戏棋,如果双方都玩到最优,那么游戏就是平局。通过进行仔细的逐个情况的分析,构造一个从不输棋而且当机会出现时总能赢棋的算法并不是困难的事。之所以能做到,是因为一些位置是已知的陷阱,可以通过查表来处理。
极小极大策略
更一般的策略是使用一个赋值函数来给一个位置的“好坏”定值。能使计算机获胜的位置可以得到值 +1;平局可得到0;使计算机输棋的位置得到值 -1.通过观察盘面就能够确定输赢的位置叫作终端位置(terminal position)。
如果一个位置不是终端位置,那么该位置的值通过递归地假设双方最优棋步而确定。这叫作极大极小策略(minimax strategy),因为下棋的一方(人)试图极小化这个位置的值,而另一方(计算机)却要使它的值达到极大。
位置p的后继位置是通过再从p走一步棋可以达到的任何位置Ps 。如果在某个位置P计算机要走棋,这就是P的值。为了得到任意后继位置Ps 的值,要递归地算出Ps 的所有后继位置的值,然后选取其中最小的值。这个最小值就代表行棋人的一方最赞成的位置。
极小极大三连游戏棋算法:计算机的选择
/** * 找出计算机最佳着法的递归函数 * 将估值返回,并给bestMove 置值,其范围 * 从1到9,表示要占据的最佳方格 * 可能的估值满足 COMP_LOSS < DRAW < COMP_WIN * 对弈人的函数 findHumanMove 见下面 */ int TicTacToe::findCompMove(int& bestMove) { int i, responseValue; int dc; //dc意为无所谓,其值用不到 int value; if (fullBoard()) value = DRAW; else if (immediateCompWin(bestMove)) return COMP_WIN; //bestMove将由 immediateCompWin置值 else { value = COMP_LOSS; bestMove = 1; for (int i = 1; i <= 9; ++i) //尝试每个方格 { if (isEmpty(i)) { place(i, COMP); responseValue = findHumanMove(dc); unplace(i); //恢复盘面 if (responseValue > value) { //更新最佳着棋 value = responseValue; bestMove = i; } } } } return value; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
极小极大三连游戏棋算法:人的选择
int TicTacToe::findHumanMove(int& bestMove) { int i, responseValue; int dc; //dc意为无所谓,其值用不到 int value; if (fullBoard()) value = DRAW; else if (immediateHumanWin(bestMove)) return COMP_LOSS; else { value = COMP_WIN; bestMove = 1; for (int i = 1; i <= 9; ++i) //尝试每个方格 { if (isEmpty(i)) { place(i, HUMAN); responseValue = findCompMove(dc); unplace(i); //恢复盘面 if (responseValue < value) { //更新最佳着棋 value = responseValue; bestMove = i; } } } } return value; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
对于更复杂的游戏,如西洋跳棋和国际象棋,搜索到终端节点的全部棋步显然是不可行的。在这种情况下,在达到递归的某个深度之后只能停止搜索。递归停止处的节点则称为终端节点,这些终端节点的值由一个估计位置的值的函数计算得出。
对于计算机下棋,一个最重要的因素看来是程序能够向前看出的棋步的数目。将其称之为层(ply),它等于递归的深度。
α - β 裁剪
/** * 执行 α- β裁剪 * 主例程应该以 * alpha =COMP_LOSS 和 beta= COMP_WIN进行调用 */ int TicTacToe::findCompMove(int& bestMove) { int i, responseValue; int dc; //dc意为无所谓,其值用不到 int value; if (fullBoard()) value = DRAW; else if (immediateCompWin(bestMove)) return COMP_WIN; //bestMove将由 immediateCompWin置值 else { value = alpha; bestMove = 1; for (int i = 1; i <= 9&& value<beta; ++i) //尝试每个方格 { if (isEmpty(i)) { place(i, COMP); responseValue = findHumanMove(dc,value,beta); unplace(i); //恢复盘面 if (responseValue > value) { //更新最佳着棋 value = responseValue; bestMove = i; } } } } return value; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
-
相关阅读:
新消费时代,零售业的进与退?
网络请求——跨域 的概念
开源云财务软件,财务软件源码,永久免费财务软件
2022CCPC绵阳站A+广东站C
Socket 编程
SpringBoot主启动类使用@ComponentScans、@ComponentScan扫描组件类,注意避坑
【linux kernel】基于ARM64分析linux内核的链接脚本vmlinux.lds.S
【linux】VMware虚拟机外网访问配置以及本机ssh连接vmware虚拟机
Linux 基本指令(上)
线性表
- 原文地址:https://blog.csdn.net/qq_51601649/article/details/125969181


