1、剑指 Offer II 072. 求平方根【科大讯飞】

题目：https://leetcode.cn/problems/jJ0w9p/
给定一个非负整数 x ，计算并返回 x 的平方根，即实现 int sqrt(int x) 函数。正数的平方根有两个，只输出其中的正数平方根。如果平方根不是整数，输出只保留整数的部分，小数部分将被舍去。
0 <= x <= 2³¹ - 1

示例 1:
输入: x = 4
输出: 2
1
2
3

输入: x = 8
输出: 2
解释: 8 的平方根是 2.82842...，由于小数部分将被舍去，所以返回 2
1
2
3

方法一：二分查找【重要】

• 时间复杂度：O(logx)
• 空间复杂度：O(1)

class Solution {
public:
    int mySqrt(int x) {
        int left = 0, right = x;
        int res = -1;
        while(left <= right){
            int mid = left + ((right - left)>>1);
            if((long long)mid * mid <= x){
                res = mid;
                left = mid + 1;
            }else right = mid - 1;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

方法二：袖珍计算器算法

「袖珍计算器算法」是一种用指数函数 exp 和对数函数 ln 代替平方根函数的方法。通过有限的可以使用的数学函数，得到想要计算的结果。

【注：由于计算机无法存储浮点数的精确值，而指数函数和对数函数的参数和返回值均为浮点数，因此运算过程中会存在误差。例如当 x = 2147395600x=2147395600 时，
因此在得到结果的整数部分 ans 后，应当找出 ans 与ans+1 中哪一个是真正的答案。】

• 时间复杂度：O(1)，由于内置的 exp 函数与 log 函数一般都很快，在这里将其复杂度视为 O(1)。
• 空间复杂度：O(1)。

class Solution {
public:
    int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }
        int ans = exp(0.5 * log(x));
        return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
    }
};
1
2
3
4
5
6
7
8
9
10

方法三：牛顿迭代

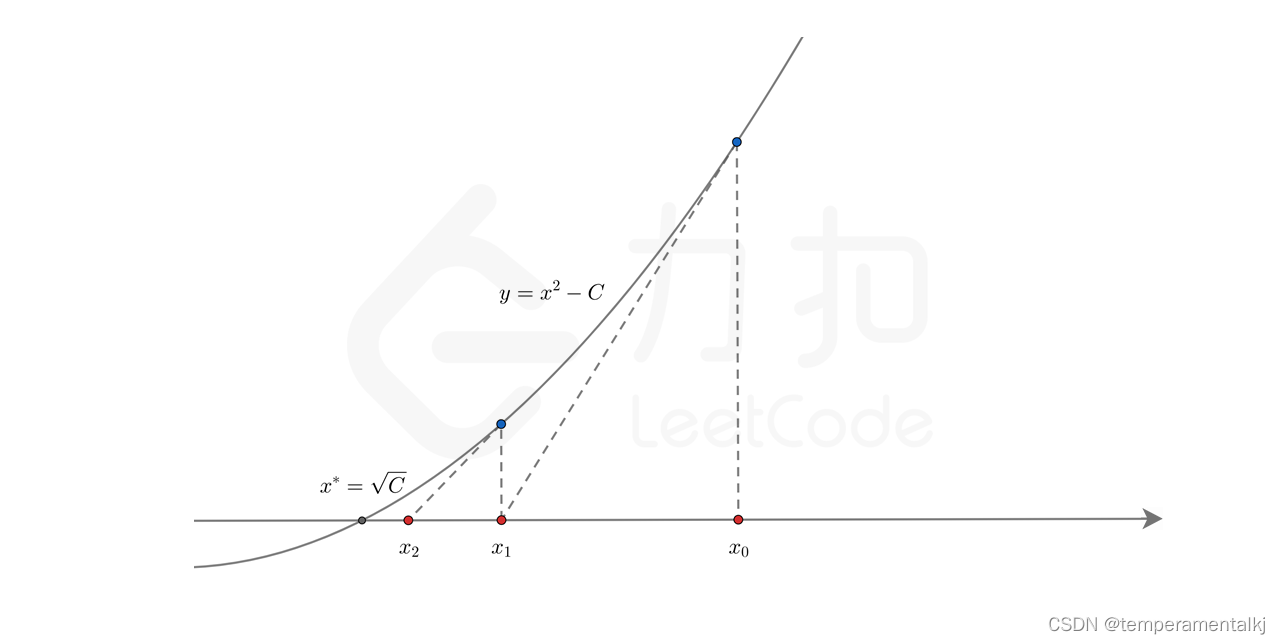
• 时间复杂度：O(logx)，此方法是二次收敛的，相较于二分查找更快。
• 空间复杂度：O(1)。

class Solution {
public:
    int mySqrt(int x) {
        if(x == 0) return 0;
        double C = x, x0 = x;
        while(true){
            double xi = 0.5*(x0 + C/x0);
            if(fabs(x0 - xi) < 1e-7) return int(xi);
            x0 = xi;
        }
        return int(x0);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13