自适应螺旋飞行麻雀搜索算法

文章目录

一、理论基础
二、仿真实验与结果分析
三、参考文献

一、理论基础

1、麻雀搜索算法

请参考这里。

2、自适应螺旋飞行麻雀搜索算法

（1）基于随机变量的Tent混沌映射

由于SSA具有随机性大的缺点，因此决定引入有序和均匀Tent映射对其进行改进。然而，基本Tent映射不是很稳定。为了减少这种影响，本文引入了基于随机变量的帐篷映射策略来改进SSA的初始化，使种群的初始化更加有序，增强了算法的可控性。其具体公式如下： $z_{i+1}=$

\begin{dcases}2z_i+\text{rand}(0,1)\times\frac1N,\quad\quad\quad\,\,\, 0\leq z_i\leq\frac12\\[2ex]2(1-z_i)+\text{rand}(0,1)\times\frac1N,\quad\frac12

\tag{1}

z_{i + 1} = ⎩ ⎪ ⎨ ⎪ ⎧ 2 z_{i} + rand (0, 1) \times \frac{1}{N}, 0 \leq z_{i} \leq \frac{1}{2} 2 (1 - z_{i}) + rand (0, 1) \times \frac{1}{N}, \frac{1}{2} < z_{i} \leq 1 (1)

经过伯努利变换后的表达式为：

z_{i+1}=(2z_i)\text{mod}\,1+\text{rand}(0,1)\times\frac1N\tag{2}

其中，

N

是混沌序列中的粒子总数。
根据Tent映射的特点，在可行域中产生混沌的序列步骤如下：
（1）随机生成

(0, 1)

中的初始值

z_0

，令

i = 1

；
（2）使用式(2)进行迭代以生成

z

序列，

i

自增1；
（3）如果迭代次数达到最大值，则停止，并保存生成的

z

序列。

（2）自适应权重

权重策略在粒子群优化算法中很常见。通常，粒子群算法通过在设定的最大值和最小值之间自适应地改变，在一定程度上减少陷入局部最优的情况。受此启发，本文在麻雀优化的发现阶段添加了惯性权重 $w$ ，该权重随迭代次数而变化。在算法的初始阶段，它削弱了随机初始化的影响，平衡了下面的Levy飞行机制，从而增强了算法的局部搜索和全局搜索。
发现者引导群体中的其他个体搜索食物，因此自适应权重的引入提高了个体位置的质量，使其他个体能够更快地收敛到最优位置，并且总体上加快了收敛速度。基于麻雀的特性，自适应权重的公式如下： $w(t)=0.2\cos\left(\frac\pi2\cdot\left(1-\frac{t}{\text{iter}_{\max}}\right)\right)\tag{3}$ 式(3)的含义是 $w$ 在 $[0, 1]$ 之间具有非线性变化的性质。根据 $\cos$ 函数的特点，算法开始时权值较小，但优化速度较快，后期权值较大，但变化速度较慢，因此算法的收敛性是平衡的。改进的发现者位置更新如下： $X_{i,j}^{t+1}=$

\begin{dcases}w(t)\cdot X_{i,j}^t\cdot\exp\left(\frac{-i}{\alpha\cdot\text{iter}_{\max}}\right),\quad\text{if}\,\,R_2<\text{ST}\\[2ex]w(t)\cdot X_{i,j}^t+Q\cdot L,\quad\quad\quad\quad\quad\quad\,\text{if}\,\,R_2\geq\text{ST}\end{dcases}

\tag{4}

X_{i, j}^{t + 1} = ⎩ ⎪ ⎨ ⎪ ⎧ w (t) \cdot X_{i, j}^{t} \cdot exp (\frac{- i}{α \cdot iter _{max}}), if R_{2} < ST w (t) \cdot X_{i, j}^{t} + Q \cdot L, if R_{2} \geq ST (4)

通过引入自适应权重来动态调整麻雀的位置变化，发现者在不同时间的不同引导模式使算法搜索灵活。随着迭代次数的增加，单个麻雀向最优位置收敛，权重越大，个体移动越快，从而提高了算法的收敛速度。

（3）莱维飞行机制

当面对高维复杂问题时，仍然存在陷入局部最优的可能性。因此，引入Levy飞行策略来提高算法解的随机性，从而丰富种群位置的多样性，还可以有效地提高算法的运行效率。
莱维飞行服从莱维分布。它使用随机长距离和短距离机制来覆盖大面积。在加入Levy飞行机制后，可以提高算法的性能。加入Levy飞行策略的位置更新公式如下： $x_i'(t)=x_i(t)+l\oplus\text{levy}(\lambda)\tag{5}$ 其中， $x_i(t)$ 表示第 $i$ 个个体在第 $t$ 次迭代中的位置； $\oplus$ 表示点到点乘法的算术符号； $l$ 表示步长控制参数，其值为 $l=0.01(x_i(t)-x_p)$ ； $\text{levy}(\lambda)$ 是服从莱维分布的路径，表示引入莱维飞行策略，并满足 $\text{levy}\sim u=t^{-\lambda},1<\lambda\leq3$ 。
由于莱维分布非常复杂，通常使用蒙特卡洛算法对其进行模拟。步长计算的公式如下： $s=\frac{\mu}{|\nu|^{1/\gamma}}\tag{6}$ $\mu\sim N(0,\sigma_\mu^2)\tag{7}$ $\nu\sim N(0,\sigma_\nu^2)\tag{8}$ $\sigma_\mu=\left\{\frac{\Gamma(1+\gamma)\sin(\pi\gamma/2)}{\gamma\cdot\Gamma[(\gamma+1)/2]\cdot2^{(\gamma+1)/2}}\right\}^{1/\gamma}\tag{9}$ 其中， $\sigma_\nu=1$ ， $\gamma=1.5$ 。

（4）可变螺旋搜索策略

跟随者随着发现者的位置而动态更新，这导致了他们搜索方式的盲目性和单一性。受鲸鱼优化算法螺旋操作的启发，引入了可变螺旋位置更新策略，以使跟随者位置更新更灵活，开发各种位置更新搜索路径，并平衡算法的全局和局部搜索。
在跟随者位置更新过程中，螺旋参数 $z$ 不能是固定数值，这导致搜索方法单调，可能陷入局部最优，从而削弱了算法的搜索能力。因此参数 $z$ 被设计为一个自适应变量，用于动态调整跟随者搜索的螺旋形状，从而拓宽了跟随者探索未知区域的能力，提高了算法的搜索效率和全局搜索性能。跟随者可变螺旋位置更新策略的公式如下： $X_{i,j}^{t+1}=$

\begin{dcases}e^{zl}\cdot\cos(2\pi l)\cdot Q\cdot\exp\left(\frac{X_{\text{worst}}^t-X_{i,j}^t}{i^2}\right),\quad\quad\quad\text{if}\,\,i>\frac n2\\[2ex]X_P^{t+1}+\left|X_{i,j}^t-X_P^{t+1}\right|\cdot A^+\cdot L\cdot e^{zl}\cdot\cos(2\pi l),\quad\text{otherwise}\end{dcases}

\tag{10}

X_{i, j}^{t + 1} = ⎩ ⎪ ⎨ ⎪ ⎧ e^{z l} \cdot cos (2 π l) \cdot Q \cdot exp (\frac{X _{worst}^{t} - X _{i, j}^{t}}{i ^{2}}), if i > \frac{n}{2} X_{P}^{t + 1} + ∣ ∣ X_{i, j}^{t} - X_{P}^{t + 1} ∣ ∣ \cdot A^{+} \cdot L \cdot e^{z l} \cdot cos (2 π l), otherwise (10)

z=e^{k\cdot\cos(\pi\cdot(1-(i/i_{\max})))}\tag{11}

其中，

k

是变化系数，

k = 5

；

l

是

[- 1, 1]

的均匀分布的随机数。随着跟随者位置更新的范围从大到小，在早期找到更多高质量的解，后期优化减少了空闲工作的增加，从而提高了算法的全局最优搜索性能。同时，根据螺旋线的特点，在一定程度上提高了算法的优化精度。

（5）改进麻雀搜索算法的步骤

自适应螺旋飞行麻雀搜索算法(ASFSSA)的具体步骤如下：
步骤1：初始化麻雀种群参数，如：种群数 $p o p$ 、发现者总数 $p N u m$ 、最大迭代次数 $\text{iter}_{\max}$ 和求解精度 $\varepsilon$ 等。
步骤2：使用式(1)的Tent映射初始化种群个体的位置，产生 $p o p$ 个麻雀个体。
步骤3：根据优化的目标函数计算每个个体的适应度值 $f_i$ ，并找到最小适应度值 $f_g$ 和最大适应度值 $f_w$ 。
步骤4：根据适应度值对群体进行排序。
步骤5：选择 $p N u m$ 个适应度较优的个体作为发现者，其余为跟随者，在添加策略后使用式(4)和(5)更新发现者的位置。
步骤6：使用式(10)更新跟随者的位置。
步骤7：使用基本麻雀算法的对应公式更新警戒者的位置。
步骤8：在一次迭代完成后，重新计算每个个体的适应度值 $f_i$ ，并更新最小适应度值 $f_g$ 、最大适应度值 $f_w$ 和相应的位置。
步骤9：判断算法是否已达到最大迭代次数或解的准确度。如果达到，则输出优化结果；否则，它将返回到步骤4。

二、仿真实验与结果分析

将ASFSSA与PSO、GWO、SSA和CSSA[2]进行对比，以文献[1]中表1的F1、F2、F3、F8、F9、F10、F16、F17、F18为例，实验设置种群规模为100，最大迭代次数为200，每种算法独立运算30次，结果显示如下：
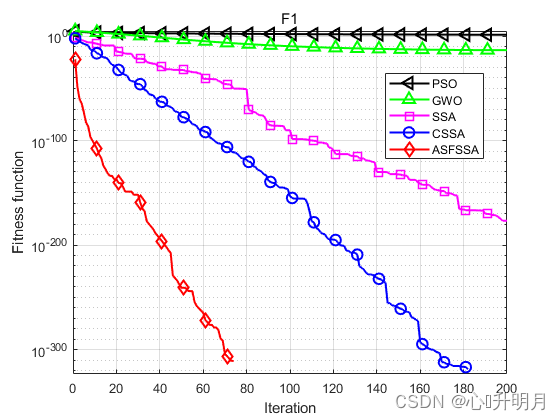
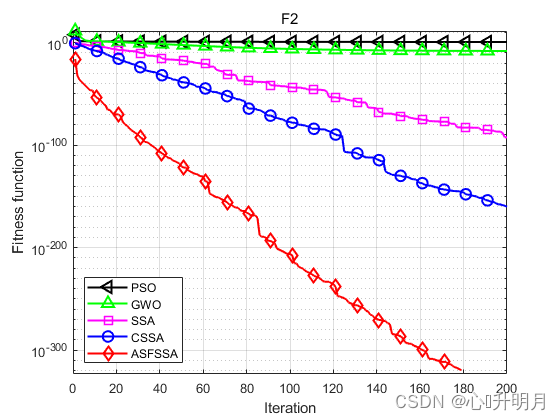
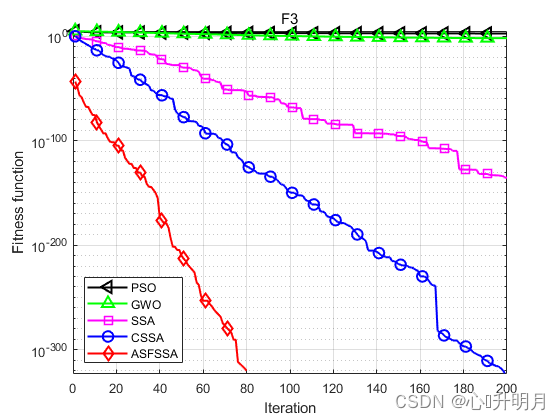
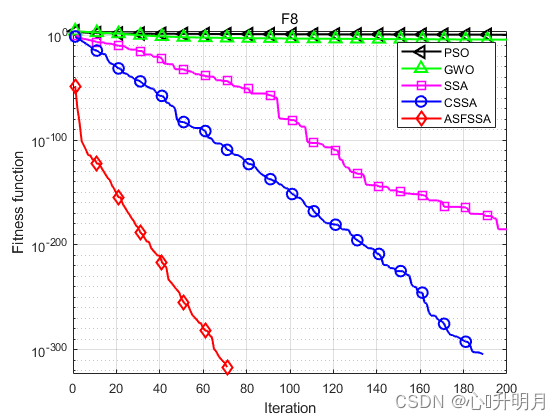
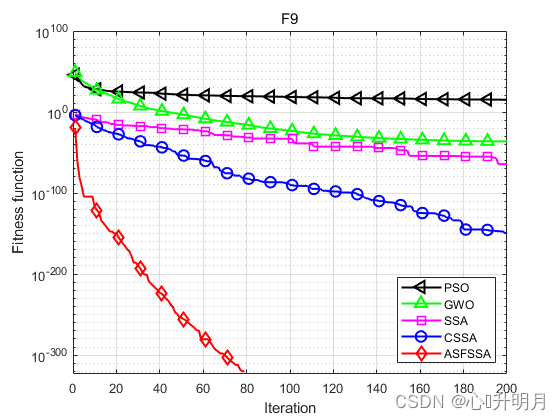
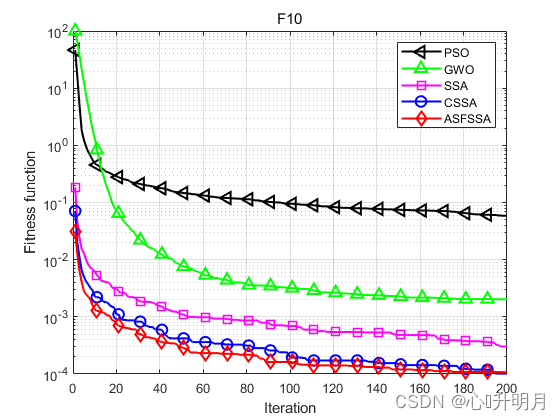
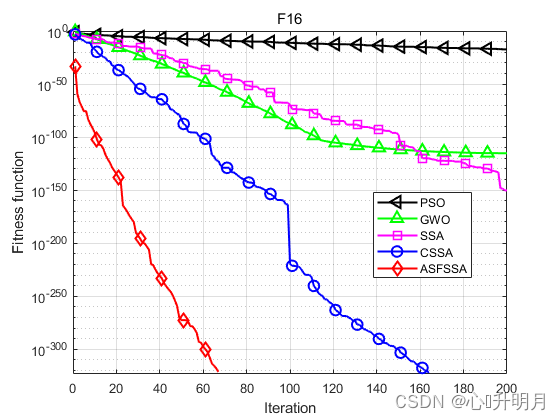
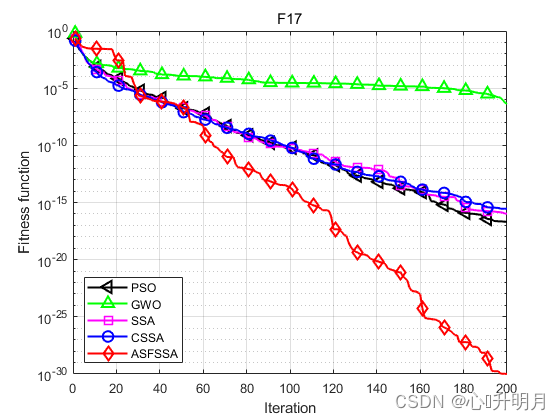
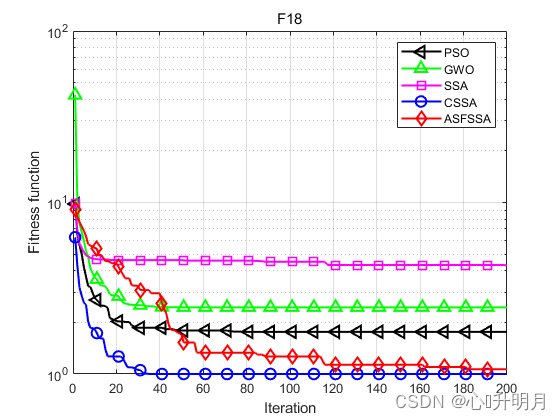
在这里插入图片描述

函数：F1
PSO：最差值: 36.2222, 最优值: 3.3372, 平均值: 13.6704, 标准差: 7.5121, 秩和检验: 1.2118e-12
GWO：最差值: 1.5074e-13, 最优值: 3.4305e-15, 平均值: 2.896e-14, 标准差: 2.7859e-14, 秩和检验: 1.2118e-12
SSA：最差值: 5.7147e-176, 最优值: 0, 平均值: 1.9049e-177, 标准差: 0, 秩和检验: 0.00066167
CSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F2
PSO：最差值: 9.7974, 最优值: 1.8171, 平均值: 4.3593, 标准差: 1.5399, 秩和检验: 1.2118e-12
GWO：最差值: 2.5083e-08, 最优值: 2.5608e-09, 平均值: 8.4577e-09, 标准差: 5.3152e-09, 秩和检验: 1.2118e-12
SSA：最差值: 9.0305e-92, 最优值: 0, 平均值: 3.5082e-93, 标准差: 1.6614e-92, 秩和检验: 5.8522e-09
CSSA：最差值: 2.1668e-159, 最优值: 0, 平均值: 7.2226e-161, 标准差: 3.956e-160, 秩和检验: 2.213e-06
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F3
PSO：最差值: 1154.4407, 最优值: 145.9255, 平均值: 436.1113, 标准差: 202.8757, 秩和检验: 1.2118e-12
GWO：最差值: 0.071841, 最优值: 0.00025149, 平均值: 0.015366, 标准差: 0.018831, 秩和检验: 1.2118e-12
SSA：最差值: 1.5258e-134, 最优值: 0, 平均值: 5.0861e-136, 标准差: 2.7858e-135, 秩和检验: 0.00031349
CSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F8
PSO：最差值: 13.4788, 最优值: 0.51689, 平均值: 3.0278, 标准差: 2.6519, 秩和检验: 1.2118e-12
GWO：最差值: 0.00016935, 最优值: 1.0188e-05, 平均值: 6.0761e-05, 标准差: 3.3525e-05, 秩和检验: 1.2118e-12
SSA：最差值: 1.4849e-184, 最优值: 0, 平均值: 4.9496e-186, 标准差: 0, 秩和检验: 0.0055843
CSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F9
PSO：最差值: 2.545785568985982e+16, 最优值: 653648260.9772, 平均值: 1102052804318338, 标准差: 4695031609008598, 秩和检验: 1.2118e-12
GWO：最差值: 1.4333e-35, 最优值: 1.0188e-45, 平均值: 5.6523e-37, 标准差: 2.6126e-36, 秩和检验: 1.2118e-12
SSA：最差值: 1.7358e-63, 最优值: 0, 平均值: 5.7861e-65, 标准差: 3.1692e-64, 秩和检验: 3.4526e-07
CSSA：最差值: 1.5716e-149, 最优值: 0, 平均值: 5.2386e-151, 标准差: 2.8693e-150, 秩和检验: 6.6096e-05
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F10
PSO：最差值: 0.12631, 最优值: 0.027397, 平均值: 0.058827, 标准差: 0.026412, 秩和检验: 3.0199e-11
GWO：最差值: 0.0047975, 最优值: 0.00039792, 平均值: 0.0020318, 标准差: 0.0011046, 秩和检验: 3.0199e-11
SSA：最差值: 0.0010802, 最优值: 3.8144e-06, 平均值: 0.00030218, 标准差: 0.00026607, 秩和检验: 0.00076973
CSSA：最差值: 0.00036871, 最优值: 1.1244e-06, 平均值: 0.00010135, 标准差: 0.00011246, 秩和检验: 0.37108
ASFSSA：最差值: 0.00036209, 最优值: 1.1872e-06, 平均值: 0.00010759, 标准差: 9.5646e-05, 秩和检验: 1
函数：F16
PSO：最差值: 4.3585e-17, 最优值: 2.7222e-21, 平均值: 4.4102e-18, 标准差: 9.0741e-18, 秩和检验: 1.2118e-12
GWO：最差值: 1.8653e-114, 最优值: 8.5392e-173, 平均值: 6.2176e-116, 标准差: 3.4055e-115, 秩和检验: 1.2118e-12
SSA：最差值: 1.2904e-149, 最优值: 0, 平均值: 6.0689e-151, 标准差: 2.5161e-150, 秩和检验: 0.00066167
CSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
ASFSSA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数：F17
PSO：最差值: 1.8263e-16, 最优值: 1.4617e-21, 平均值: 2.0378e-17, 标准差: 4.0282e-17, 秩和检验: 2.3692e-11
GWO：最差值: 2.7542e-06, 最优值: 8.1184e-09, 平均值: 4.2415e-07, 标准差: 5.374e-07, 秩和检验: 2.3692e-11
SSA：最差值: 1.3593e-15, 最优值: 2.8125e-21, 平均值: 1.0532e-16, 标准差: 3.3378e-16, 秩和检验: 2.3692e-11
CSSA：最差值: 7.7736e-15, 最优值: 3.0315e-22, 平均值: 2.8089e-16, 标准差: 1.4159e-15, 秩和检验: 2.3692e-11
ASFSSA：最差值: 1.9909e-29, 最优值: 0, 平均值: 1.0365e-30, 标准差: 3.6905e-30, 秩和检验: 1
函数：F18
PSO：最差值: 6.9033, 最优值: 0.998, 平均值: 1.7576, 标准差: 1.2063, 秩和检验: 0.0055747
GWO：最差值: 10.7632, 最优值: 0.998, 平均值: 2.4428, 标准差: 2.4451, 秩和检验: 1.2224e-10
SSA：最差值: 12.6705, 最优值: 0.998, 平均值: 4.2858, 标准差: 5.0449, 秩和检验: 0.10391
CSSA：最差值: 0.998, 最优值: 0.998, 平均值: 0.998, 标准差: 1.934e-16, 秩和检验: 0.0011992
ASFSSA：最差值: 2.9821, 最优值: 0.998, 平均值: 1.0641, 标准差: 0.36225, 秩和检验: 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

实验结果验证了ASFSSA算法的有效性。

三、参考文献

[1] Chengtian Ouyang, Yaxian Qiu, Donglin Zhu. Adaptive Spiral Flying Sparrow Search Algorithm[J]. Scientific Programming, 2021, 2021: 6505253.
[2] 吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021, 47(8): 1712-1720.

相关阅读:
什么是“空洞卷积”
Cpp创建桌面快捷方式lnk
轮式装载机铲斗模拟仿真
SpringBoot框架Mockito的使用
【vue3】Transition过渡组件
Manacher算法
Jdbc初测试（一）
测试用例：在线音乐播放器
初识 MySQL 数据库
【动态规划】按位与最大的最长子数组

原文地址：https://blog.csdn.net/weixin_43821559/article/details/126052765