【32. 图中的层次(图的广度优先遍历)】

图中的层次

思路

• 因为所有的边长都为1，所以可以使用宽度优先搜索的思想，每当队列pop出一个元素时，将其距离为1的节点都加到队列中（层次遍历思想）
• st[]标记各个节点有没有走过，d[]保存1号节点到各个节点的距离，初始时都为-1。

难点

• 如何进行层次遍历？

首先需要将图，变成邻接表进行存储。可参照之前写的数组模拟链表，数组模拟链表只是一个头结点，而图的是有n个头结点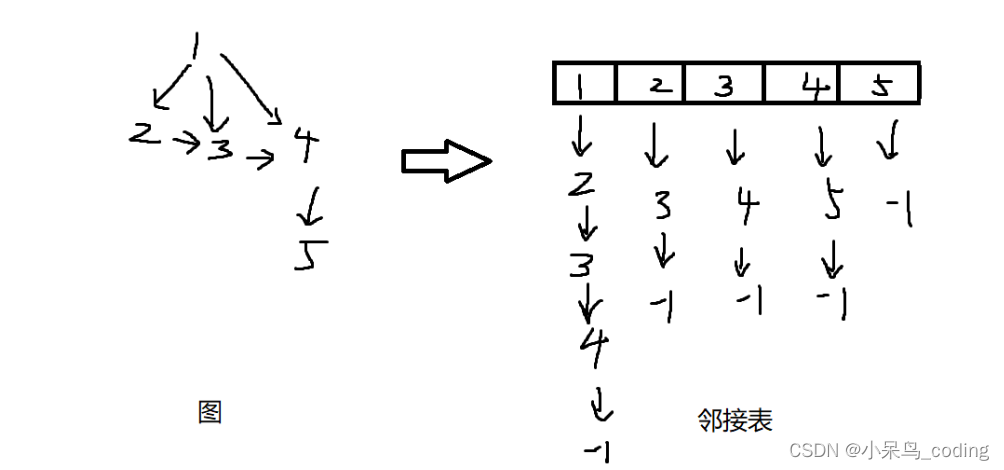

• 图中的数组是一个存储头结点，我们给定一个节点1，那么在h[1]指向的这条链表上，都是与节点1相邻的节点（即距离为1）。
• 因此，在pop出一个节点t时，只需使用h[t]指向它的链表，再通过for(int i = h[t]; i != -1; i = ne[i])，就可以遍历一整条链表上的节点。然后在遍历时将其加到队列中，并将其的长度置位h[t]+1即可；

for (int i = h[t]; i != -1; i = ne[i]) // ne[i]上的点都是与i节点距离为1的点
        {
            int j = e[i]; // 向外走一步
            if (d[j] == -1) // 如果j没有被遍历过
            {
                d[j] = d[t] + 1; // 因为路径长度都是1，所以直接在上一步的基础上加上1即可
                q.push(j); // 将j加到队列中
            }
        }
1
2
3
4
5
6
7
8
9

步骤

1. 1 号节点入队列，dist[1] 的值更新为 0。
2. 如果队列非空，就取出队头，找到队头节点能到的所有节点。(也就是遍历一条链表上的所有节点，遍历时将这些节点入队)
3. 如果队头节点能到走到的节点没有标记过，就将节点的dist值更新为队头的d[]值+1，然后入队。
4. 重复步骤 2，3 直到队列为空。
5. d[]中就存储了 1 号节点到各个节点的距离了。如果距离是无穷大，则不能到达，输出 -1，如果距离不是无穷大，则能到达，输出距离。

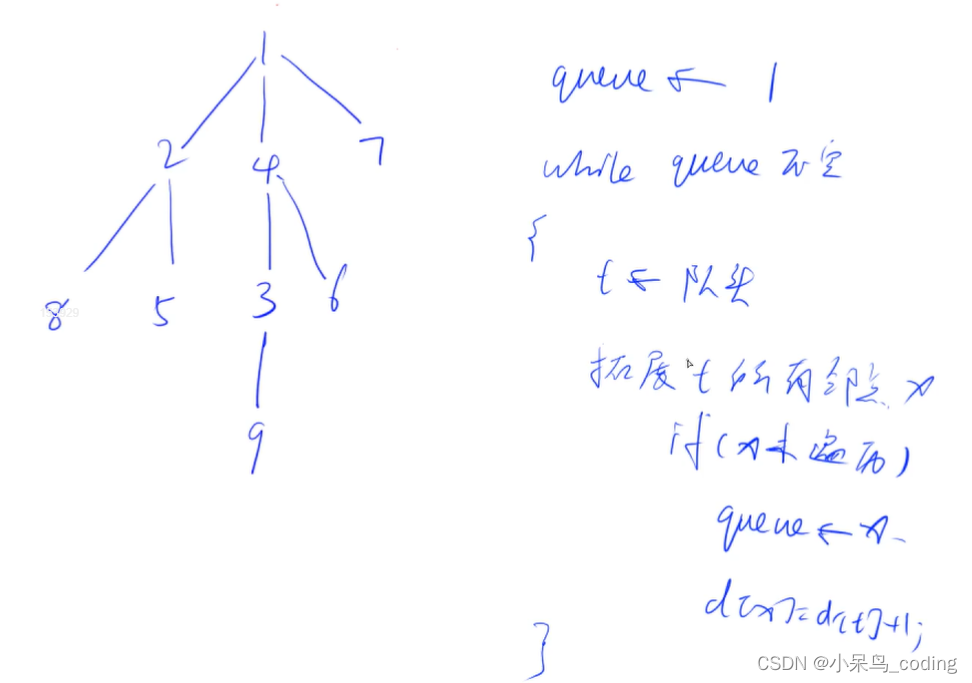
注意

• 边权都是1才能使用bfs搜索最短路径
• 因为计算机一次性只能处理一个，但是最短路径要求层次遍历，也就是一次性处理多个。此时需要用到队列，来存储这些层次节点（例如上述图中从1号节点，往下走一层，此时走过的点有2, 3，4，这些都是与1号节点距离为1，所以依次将他们入队，距离设置为1.然后再反复运行，直到队列为空）

对于重边和自环解决办法

• 在一开始add时，会把重边和自环add进去，但是后面访问的时候，设置了一个用来判断是否被访问过的数组st[]来记录图中每个点是否被访问过的
  所以这样抵消了重边和自环的影响，也即不会多次访问同一个点。

题目

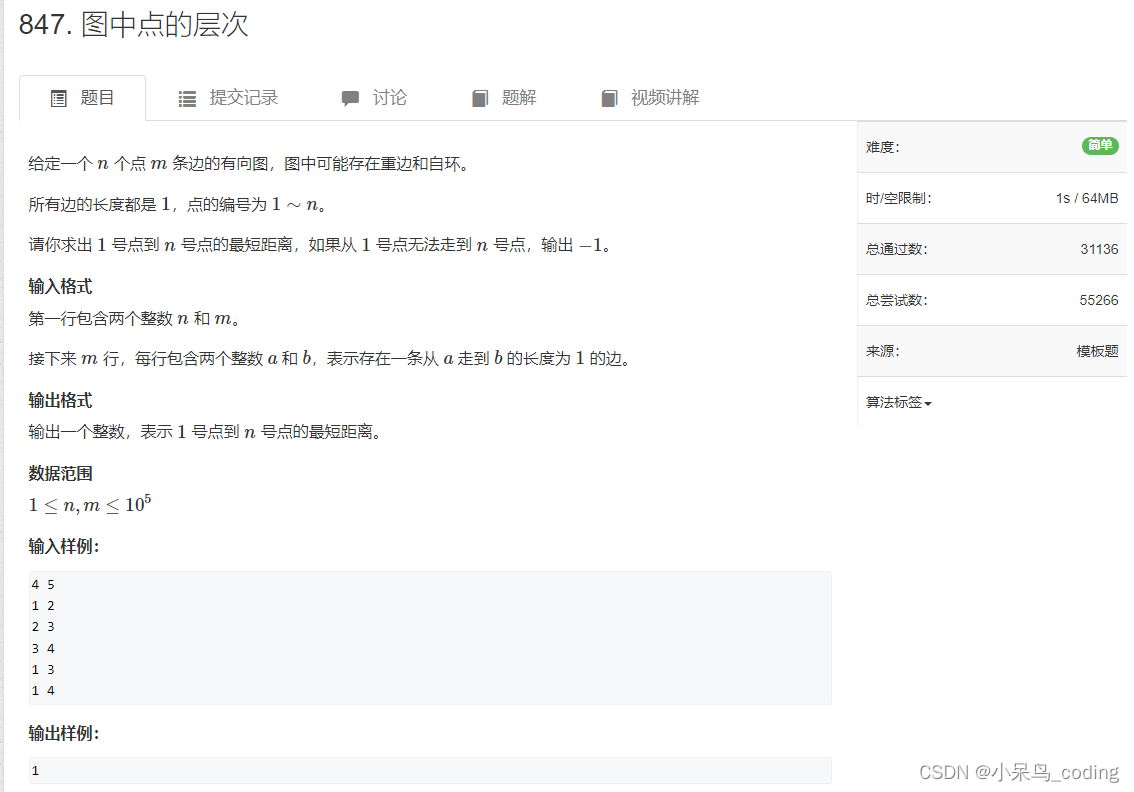
代码

#include 
#include 
#include 
#include 
using namespace std;

const int N = 100010;

int h[N],ne[N], e[N], idx;//邻接表数据结构
int d[N];//存储距离
int st[N];//标记点是否走到过
int n, m;

void add(int a, int b)//邻接表存储图
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int bfs()
{
    memset(d, -1, sizeof(d));//初始都没有走到过，距离无穷大
    d[1] = 0;//从1号节点开始，距离为0
    queue<int> q;//队列
    q.push(1);//1号节点入队列
    st[1] = 1;//1到1的距离为0，已经求出
    
    while(q.size())//对列非空，就一直往后搜索
    {
        int t = q.front();//队头出队，找该点能到的点
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i])//遍历所有t节点能到的点，i为节点索引
        {
            int j = e[i];//通过索引i得到t能到的节点编号
            if(!st[j])//如果没有遍历过
            {
                d[j] = d[t] + 1;//距离为t号节点的距离+1
                q.push(j);//节点入队
                st[j] = 1;//入队后标记，已经遍历过了
            }
        }
    }
    return d[n];
}

int main()
{
    cin >> n >>m;
    memset(h, -1, sizeof h);//初始化，所有节点没有后继，后继都是-1
    for(int i = 0; i < m; i++)//读入所有边
    {
        int a, b;
        cin >> a >> b;
        add(a, b);//加入邻接表
    }
   cout <<  bfs();//广度优先遍历

    
    return 0;
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61