---

前言

给定一个有正、有负、有0的数组arr，
给定一个整数k，
返回arr的子集是否能累加出k
1）正常怎么做？
2）如果arr中的数值很大，但是arr的长度不大，怎么做？

题目一

子集就是子序列
每一个位置的数要跟不要展开生成的子序列就对应一个子集.
标准的从左往右的尝试模型

dp[i][j]:
arr 0~i范围的数自由选择能不能累加出j这个累加和来,是一 张true, false表,分情况讨论:
1)完全不用i位置的数, dpl[i-1][j]
2)-定要含有i位置的数, dp[i- 1]lj-arr[i]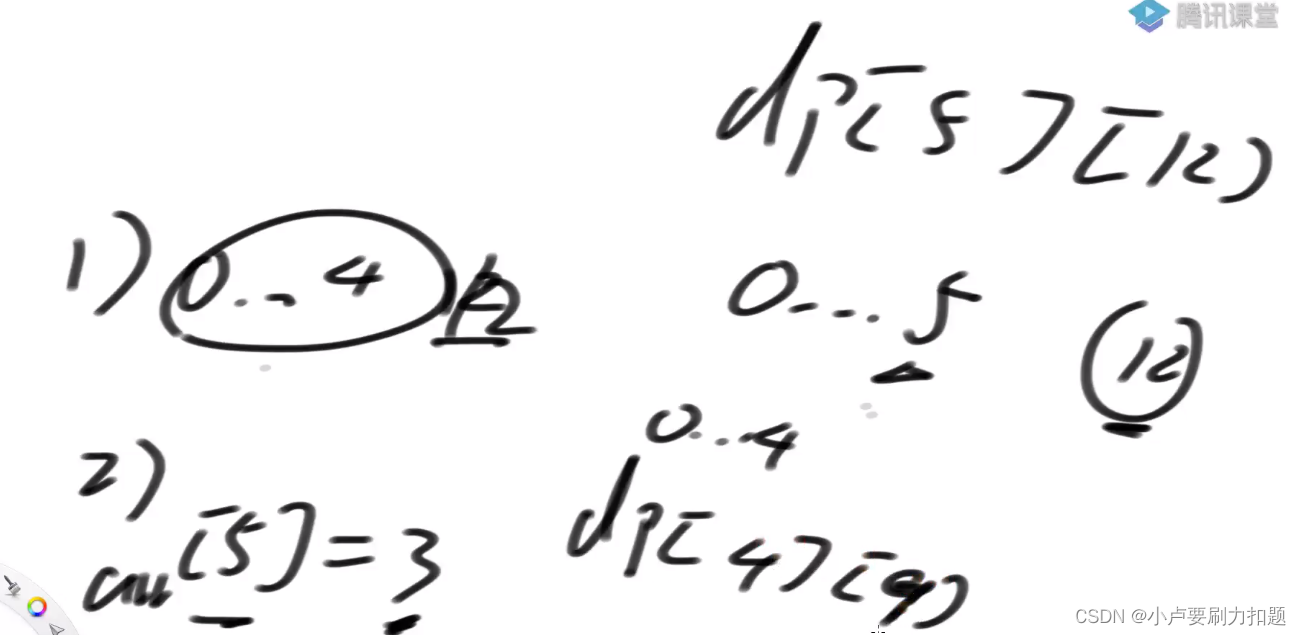

求dp[5][12]

1)0~4搞出12
2)用5位置的3, 0~4搞出9

列的大小不能按K的大小来

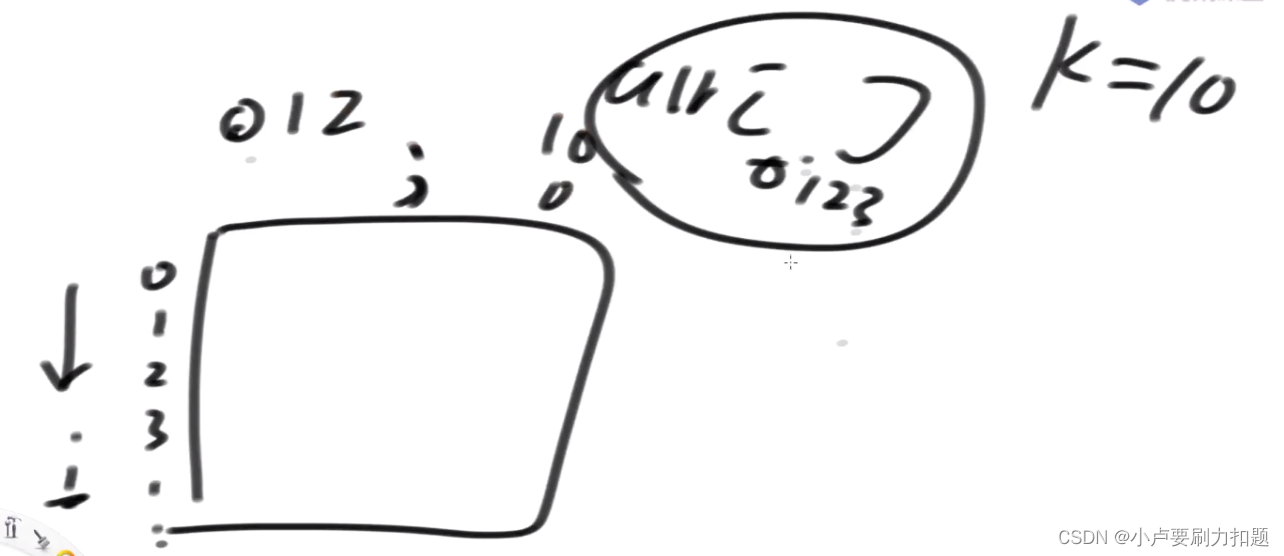
如果arr里只有正数,列值搞到K= 10就够了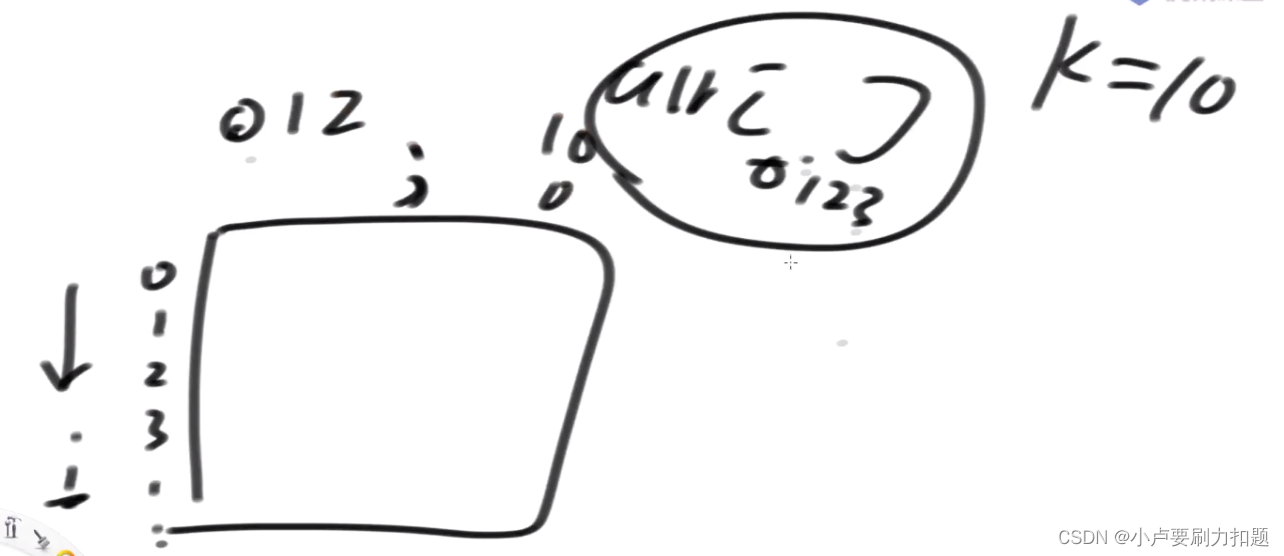

难点在于有正、有负、有0,只定义0~K是不够的,有负数列的大小不能够按照K的大小来决定
把所有负数累加到一起,所有正数累加到一起 这样累加和可能范围就定下来了

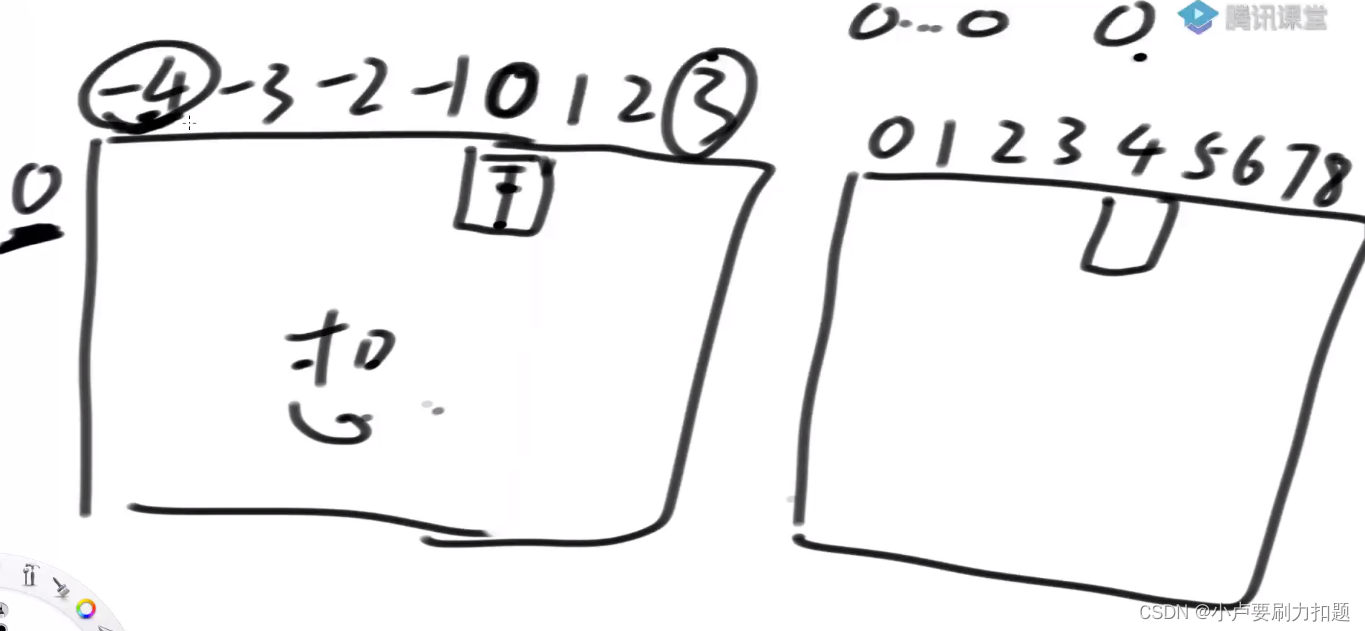
平移对应
想象中dp[i][j]的值实际要拿dp[i][j-min]的值

代码

	public static boolean isSum3(int[] arr, int sum) {
		if (sum == 0) {
			return true;
		}
		// sum != 0
		if (arr == null || arr.length == 0) {
			return false;
		}
		int min = 0;
		int max = 0;
		for (int num : arr) {
			min += num < 0 ? num : 0;
			max += num > 0 ? num : 0;
		}
		// min~max
		if (sum < min || sum > max) {
			return false;
		}

		// min <= sum <= max
		int N = arr.length;
		boolean[][] dp = new boolean[N][max - min + 1];
		// dp[0][0] = true
		dp[0][-min] = true;
		dp[0][arr[0] - min] = true;
		for (int i = 1; i < N; i++) {
			for (int j = min; j <= max; j++) {
				dp[i][j - min] = dp[i - 1][j - min];
				int next = j - min - arr[i];
				dp[i][j - min] |= (next >= 0 && next <= max - min && dp[i - 1][next]);
			}
		}
		return dp[N - 1][sum - min];
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

问题二解决思路

第二问使用的是分治思想

这个表列需要从最小值一直推到最大值如果arr中值很大,会导致列非常多，
整张表有可能算不完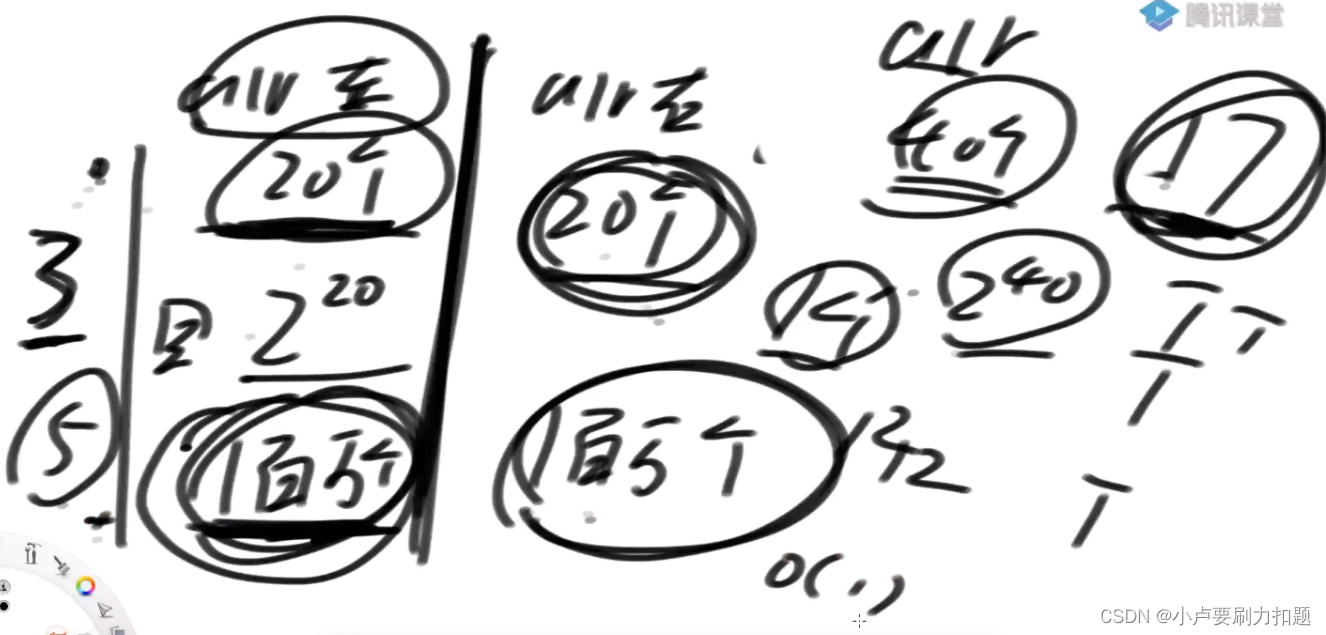

假设arr长度40,如果不切成左右两半2^40,程序是跑不完的
分左右两半,每边20个数跑暴力每个数要跟不要都展开(2^20),收集所有累加和
左边20个数暴力的方式跑出来100万个累加和,
右边20个数暴力的方式跑出来100万个累加和，
问arr 40个数任意选你能不能搞定某个累加和17怎么算?
如果单独左边,右边可以搞定17就返回T,否则
左右两侧凑,想一个整合逻辑
遍历左边所有可能的累加和一百万个。但是当我一旦确定一个累加和的时候，
我在右边找他所伴随的累加和是非常快的。
比如左边3,右边凑14
0(1)

	public static boolean isSum(int[] arr, int sum) {
		if (sum == 0) {
			return true;
		}
		if (arr == null || arr.length == 0) {
			return false;
		}
		if (arr.length == 1) {
			return arr[0] == sum;
		}
		int N = arr.length;
		int mid = N >> 1;
		HashSet<Integer> leftSum = new HashSet<>();
		HashSet<Integer> rightSum = new HashSet<>();
		process4(arr, 0, mid, 0, leftSum);
		process4(arr, mid, N, 0, rightSum);
		// 单独查看，只使用左部分，能不能搞出sum
		// 单独查看，只使用右部分，能不能搞出sum
		// 左+右，联合能不能搞出sum
		// 左部分搞出所有累加和的时候，包含左部分一个数也没有，这种情况的，leftsum表里，0
		for (int l : leftSum) {
			if (rightSum.contains(sum - l)) {
				return true;
			}
		}
		return false;
	}
	// arr[0...i-1]决定已经做完了！形成的累加和是pre
	// arr[i...end - 1] end(终止)  所有数字随意选择，
	// arr[0...end-1]所有可能的累加和存到ans里去
	public static void process4(int[] arr, int i, int end, int pre, HashSet<Integer> ans) {
		if (i == end) {
			ans.add(pre);
		} else {
			process4(arr, i + 1, end, pre, ans);
			process4(arr, i + 1, end, pre + arr[i], ans);
		}
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38