1、定义

方差分析是检验多个总体的均值是否相等来判断分类型自变量对数值型因变量是否有影响。

名字是方差分析，其实主要是比较总体的均值，在判断均值是否有差异时要借助方差。

它的优点是可以增加分类的可靠性。如果要研究4个总体的均值那么要两两比较需要比较6次，如果每次犯第一类错误的概率都是0.05，那么随着实验次数的增多会增大犯错误的概率。一般来说，随着增加个体显著性检验的次数，偶然因素导致差别的可能性也会增大(并非均值真的存在差别)，而方差分析就是同时考虑所有的样本，因此排除了错误累积的概率，从而避免拒绝一个真实的原假设。

其实方差分析是通过对数据误差来源的分析来判断不同总体的均值是否相等从而来分析自变量是否对因变量有显著影响。
误差主要有两个来源：

• 一是组内误差(SSE)
• 二是组间误差(SSA)。
  组内误差就是由于随机因素造成的组内随机误差，组间误差就是不同水平之间的误差，这种误差可能是由于随机性导致的也可能是由于本身的系统性误差导致的，误差是用平方和来表示的。总的误差为SST，有SST=SSE+SSA，也就是说，如果不同水平之间没有差异，那么组间误差就应该近似等于组内误差，比值就会接近1，而如果本身存在差异那说明还存在系统误差，这样比值就会>1，比值越大说明水平之间的差异越大，这样说明自变量确实对因变量有影响。

基本假定：

• 每个总体应该服从正态分布
• 各个总体的方差必须相同
• 观测值是独立的

2、分析步骤

方差分析中的误差可以拆解为两部分：SST=SSE+SSA

总平方和SST为全部观测值与总均值的误差平方和，组间平方和SSA为各组均值与总均值的误差平方和，组内平方和SSE为各组观测值与各组均值的误差平方和，用到的是F统计量。

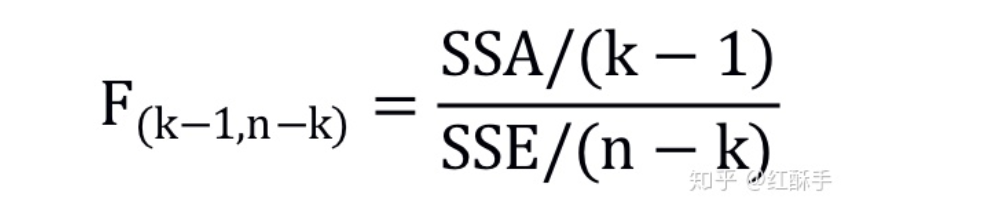参考链接：https://zhuanlan.zhihu.com/p/195690968

跟临界值比较，若计算出来的统计量的值>临界值，那么要拒绝原假设，也即不同水平之间有显著差异(差异越大值越大)，否则就不拒绝原假设。