手写深度学习之优化器（SGD、Momentum、Nesterov、AdaGrad、RMSProp、Adam）

SGD

SGD全称为随机梯度下降法（Stochastic Gradient Descent），一个经典的例子就是假设你现在在山上，为了以最快的速度下山，且视线良好，你可以看清自己的位置以及所处位置的坡度，那么沿着坡向下走，最终你会走到山底。但是如果你被蒙上双眼，那么你则只能凭借脚踩石头的感觉判断当前位置的坡度，精确性就大大下降，有时候你认为的坡，实际上可能并不是坡，走一段时间后发现没有下山，或者曲曲折折走了好多路才能下山。

梯度下降的过程，就好像我们用学习率为 $\alpha$ 的步长一步步地向山谷的大致方向移动，我们每一步只能向山谷的方向靠近，每一步都在进步，整个过程可以参考下面的动图
在这里插入图片描述

小球从山顶从不同的方向梯度滚下山，这就是梯度下降的过程。但是梯度下降算法每一步的更新都需要计算所有超参数的梯度（即批量梯度下降法（Batch Gradient Descent，BGD），需要在全部训练集上计算准确的梯度），迭代速度必然会很慢，那么没有更快的方法呢？可以采用随机梯度下降法（（Stochastic gradient descent，SGD）），所谓的随机二字，就是说我们可以随机用一个样本来表示所有的样本，即采样单个样本来估计当前的梯度。批量梯度下降法（Batch Gradient Descent，BGD）就好比正常下山，而随机梯度下降法就好比蒙着眼睛下山。

因为这个样本是随机的，所以每次迭代没有办法得到一个准确的梯度，这样一来虽然每一次迭代得到的损失函数不一定是朝着全局最优方向，但是大体的方向还是朝着全局最优解的方向靠近，直到最后，得到的结果通常就会在全局最优解的附近。这种算法相比普通的梯度下降算法，收敛的速度更快，所以在一般神经网络模型训练中，随机梯度下降算法 SGD 是一种非常常见的优化算法。

随机梯度下降的公式如下：

$\mu \frac{\partial L}{\partial W}$

其中 $W$ 为需要更新的权重，损失函数关于 $W$ 的梯度记为 $\frac{\partial L}{\partial W}$ ， $\mu$ 表示学习率。

代码实现

class SGD:
    """
    SGD
    """
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key] 
1
2
3
4
5
6
7
8
9
10

动量梯度下降法

Momentum动量

动量法，基本迭代公式可以描述为：

$v_{t} = \mu_{t-1} v_{t-1} - \varepsilon _{t-1} \nabla _{f}(\theta _{t-1})$
$\theta _{t} = \theta _{t-1} + v_{t}$

其中 $\theta _{t}$ 是模型参数，这里的 $\mu _{t-1}$ 表示衰减因子，可以理解为对以前方向的依赖程度，注意到如果 $\mu _{t-1}=0$ ，那就变成了普通的梯度方法了。 $\varepsilon _{t}>0$ 表示在每次迭代时候的学习率。 $f_{(\theta )}$ 是目标函数。 $\nabla _{f}({\theta }' )$ 是梯度 $\frac{\partial f(\theta )}{\partial \theta } | _{\theta ={\theta }' }$ 的速记符号
在不同的文献会看到不同的实现方式，比如把减号换个位置

$v_{t} = \mu_{t-1} v_{t-1} + \varepsilon _{t-1} \nabla _{f}(\theta _{t-1})$
$\theta _{t} = \theta _{t-1} - v_{t}$

有时会看到下面这种写法，也就是将学习率写在更新项上（第二行）:

$v_{t} = \mu_{t-1} v_{t-1} + \nabla _{f}(\theta _{t-1})$
$\theta _{t} = \theta _{t-1} - \varepsilon _{t-1}v_{t}$

代码实现

class Momentum:

    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Nesterov加速

Nesterov加速算法（Nesterov Accelerated Gradient）中：算法能够在目标函数有增高趋势之前，减缓更新速率。 算法思想是：

在先前累计的梯度上进行一个大跳跃
然后测量最后的梯度并进行矫正

如上图（图片来自这里）所示，蓝色箭头表示传统的Momentum算法计算，其中当前梯度（短蓝向量）和动量项（长蓝向量）。然而，既然已经利用了动量项来更新，那不妨先计算出下一时刻 $\theta$ 的近似位置（棕向量），并根据该未来位置计算梯度（红向量），然后使用和传统的Momentum算法中相同的方式计算步长（绿向量）。这种计算梯度的方式可以使算法更好的「预测未来」，提前调整更新速率。

图片来自这里

Nesterov算法的好处是：当梯度方向快要改变的时候，它提前获得了该信息，从而减弱了这个过程，再次减少了无用的迭代。

Nesterov加速方法的基本迭代形式为:

(1):
$v_{t} = μ_{t - 1} v_{t - 1} - ε_{t - 1} \nabla_{f} (θ_{t - 1} + μ_{t - 1} v_{t - 1})$
(2):
$θ_{t} = θ_{t - 1} + v_{t}$
和动量方法的区别在于二者用到了不同点的梯度，动量方法采用的是上一步 $\theta _{t-1}$ 的梯度方向，而Nesterov加速方法则是从 $\theta _{t-1}$ 朝着 $v_{t-1}$ 往前一步（向前看，peeking ahead）。一种解释是，反正要朝着 $v_{t-1}$ 方向走，不如先利用了这个信息，这个叫未卜先知。

我们定义一个peeking ahead参数：

(3):
$Θ_{t - 1} \equiv θ_{t - 1} + μ_{t - 1} v_{t - 1}$

那么上面 (1)、(2) 公式可以转化为：

(4):——从(1)推导而来
$v_{t} = μ_{t - 1} v_{t - 1} - ε_{t - 1} \nabla_{f} (Θ_{t - 1})$
(5):——从(3)推导而来
$Θ_{t} = θ_{t} + μ_{t} v_{t} = (θ_{t - 1} + v_{t}) + μ_{t} v_{t} = (Θ_{t - 1} - μ_{t - 1} v_{t - 1}) + v_{t} + μ_{t} v_{t} = Θ_{t - 1} - μ_{t - 1} v_{t - 1} + (1 + μ_{t}) v_{t} = Θ_{t - 1} - μ_{t - 1} v_{t - 1} + (1 + μ_{t}) (μ_{t - 1} v_{t - 1} - ε_{t - 1} \nabla_{f} (Θ_{t - 1})) = Θ_{t - 1} - μ_{t - 1} v_{t - 1} + (1 + μ_{t}) μ_{t - 1} v_{t - 1} - (1 + μ_{t}) ε_{t - 1} \nabla_{f} (Θ_{t - 1}) = Θ_{t - 1} + μ_{t} μ_{t - 1} v_{t - 1} - (1 + μ_{t}) ε_{t - 1} \nabla_{f} (Θ_{t - 1})$

上述公式的推导来自论文：ADVANCES IN OPTIMIZING RECURRENT NETWORKS，假设初始速度 $v_{1}=0$ 时候，优化的收敛速度 $v_{T}\simeq 0$ (近似等于0)，参数 ${\color{Red}\Theta}$ 等同于 ${\color{Red}\theta}$ ，那么上述公式可以转化为:

θ_{t} = θ_{t - 1} + μ_{t} μ_{t - 1} v_{t - 1} - (1 + μ_{t}) ε_{t - 1} \nabla_{f} (θ_{t - 1})

我们回顾一下基本的Momentum动量公式如下：
$θ_{t} = θ_{t - 1} + μ_{t - 1} v_{t - 1} - ε_{t - 1} \nabla_{f} (θ_{t - 1})$

我们对比上述公式(6)和公式(7)可以发现：公式(6)等同于公式(7)乘上了不同的线性系数（公式7中的 $\mu_{t-1}v_{t}$ 如果乘上 $\mu_{t}$ 、 $\varepsilon _{t-1} \nabla _{f}(\theta _{t-1})$ 如果乘上 $(1+\mu_{t})$ 则与公式(6)等价）。

Nesterov

class Nesterov:

    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
            
        for key in params.keys():
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

AdaGrad 算法

在神经网络的学习中，学习率（数学式中记为 $\mu$ ）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。
AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习（AdaGrad的Ada来自英文单词Adaptive，即“适当的”的意思）。下面，让我们用数学式表示AdaGrad的更新方法:

$\frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W}$
$\eta \frac{1}{\sqrt{h} }\frac{\partial L}{\partial W}$

和前面的SGD一样， $W$ 表示要更新的权重参数， $\frac{\partial L}{\partial W}$ 表示损失函数关于 $W$ 的梯度， $\eta$ 表示学习率。这里新出现了变量 $h$ ，如上所示，它保存了以前的所有梯度值的平方和，上面公式中的 $\odot$ 表示对应矩阵元素的乘法）。然后，在更新参数时，通过乘以 $\frac{1}{\sqrt{h} }$ ，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。

假设我们现在采用的优化算法是最普通的梯度下降法mini-batch。它的移动方向如下面蓝色所示：
在这里插入图片描述
假设我们现在就只有两个参数w,b，我们从图中可以看到在b方向走的比较陡峭，这影响了优化速度。
而我们采取AdaGrad 算法之后，我们在算法中使用了累积平方梯度：

$\frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W}$

从上图可以看出在b方向上的梯度g要大于在w方向上的梯度。

那么在下次计算更新的时候， $h$ 是作为分母出现的，越大的反而更新越小，越小的值反而更新越大，那么后面的更新则会像下面绿色线更新一样，明显就会好于蓝色更新曲线。
在这里插入图片描述
从直观上看，在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

代码

class AdaGrad:
    """AdaGrad算法
    """
    def __init__(self, lr=0.01) -> None:
        self.lr = lr
        self.h = None
    
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            # 防止除数为0，加上1e-7
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

RMSprop算法

AdaGrad会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境地学习，更新量就会变为 0，完全不再更新。为了改善这个问题，可以使用 RMSProp方法（Root Mean Square Prop，是Geoffrey E. Hinton在cs321课程中提出的一种优化算法）。RMSProp方法并不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。
这种操作从专业上讲，称为“指数移动平均”，呈指数函数式地减小过去的梯度的尺度，关于指数移动平均的相关知识可以参考这篇博客。

在AdaGrad算法中，我们介绍计算公式为：

h = h + \frac{\partial L}{\partial W} ⊙ \frac{\partial L}{\partial W} W = W - η \frac{1}{h} \frac{\partial L}{\partial W}

而RMSprop算法的计算公式与AdaGrad公式只在计算 $h$ 时候存在区别：

h = γ h + (1 - γ) \frac{\partial L}{\partial W} ⊙ \frac{\partial L}{\partial W} W = W - η \frac{1}{h} \frac{\partial L}{\partial W}

代码

class RMSprop:

    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr   # 学习率
        self.decay_rate = decay_rate    # 衰减系数
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Adam算法

Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参数的每个元素适当地调整更新步伐，如果将这两个方法融合在一起会怎么样?Adam算法就是这样的思路，直观地讲，就是融合了Momentum和AdaGrad的方法。通过组合前面两个方法的优点，有望实现参数空间的高效搜索。

Adam算法的计算公式如下：

$t=t+1gt=∇θft(θt−1)【在t时刻得到关于随机目标的梯度】mt=β1mt−1+(1−β1)gt【更新有偏一阶矩估计】vt=β2vt−1+(1−β2)g2t【更新有偏二阶矩估计】^mt=mt/(1−βt1)【计算偏差校正的一阶矩估计】^vt=vt/(1−βt2)【计算偏差校正的二阶矩估计】θt=θt−1−α⋅^mt/(√^vt+ε)【更新参数】$

t g_{t} m_{t} v_{t} \overset{m_{t}}{^} \overset{v_{t}}{^} θ_{t} = t + 1 = \nabla_{θ} f_{t} (θ_{t - 1}) 【在 t 时刻得到关于随机目标的梯度】 = β_{1} m_{t - 1} + (1 - β_{1}) g_{t} 【更新有偏一阶矩估计】 = β_{2} v_{t - 1} + (1 - β_{2}) g_{t}^{2} 【更新有偏二阶矩估计】 = m_{t} / (1 - β_{1}^{t}) 【计算偏差校正的一阶矩估计】 = v_{t} / (1 - β_{2}^{t}) 【计算偏差校正的二阶矩估计】 = θ_{t - 1} - α \cdot \overset{m_{t}}{^} / (\overset{v_{t}}{^} + ε) 【更新参数】

上述每个步骤的含义如下：

首先，计算梯度的指数移动平均数， $m_{0}$ 初始化为0。类似于Momentum算法，综合考虑之前时间步的梯度动量。 $\beta_{1}$ 系数为指数衰减率，控制权重分配（动量与当前梯度），通常取接近于1的值，默认为0.9。

$m_{t} = \beta _{1}m_{t-1} + (1-\beta _{1})g_{t} 【更新有偏一阶矩估计】$

计算梯度平方的指数移动平均， $v_{0}$ 初始化为0， $\beta_{2}$ 系数为指数衰减率，控制之前的梯度平方的影响情况，类似RMRProp算法，对梯度平方进行加权权值。默认为0.999.

$v_{t}= \beta _{2}v_{t-1} + (1-\beta _{2})g_{t}^2 【更新有偏二阶矩估计】$

由于 $m_{0}$ 初始化为0，会导致 $m_{t}$ 偏向于0，尤其在训练初期阶段。所以，此处需要对梯度均值 $m_{t}$ 进行偏差纠正，降低偏差对训练初期的影响，其中 $\beta _{1}^{t}$ 表示 $\beta _{1}$ 的 $t$ 次方。

$\hat{m_{t}} = \frac{m_{t}}{1-\beta _{1}^{t}}$

与 $m_{0}$ 类似，因为 $v_{0}$ 初始化为0，导致训练初始阶段 $v_{t}$ 偏向0，对其进行纠正，其中 $\beta _{2}^{t}$ 表示 $\beta _{2}$ 的 $t$ 次方

$\hat{v_{t}} = \frac{v_{t}}{1-\beta _{2}^{t}}$

更新参数，初始的学习率 $\alpha$ 乘以梯度均值与梯度方差的平方根之比。其中默认学习率 $\alpha=0.001$ , $\varepsilon=10^{-8}$ ，避免除数变为0。由表达式可以看出来，对更新的步长计算，能够从梯度均值以及梯度平方两个角度进行自适应调节，而不是直接由当前梯度决定。
$\theta _{t} = \theta _{t-1} - \alpha \cdot \frac{\hat{m_{t}}}{(\sqrt{\hat{v_{t}}} + \varepsilon )}$

Adam的好处主要有：

实现简单，计算高效，对内存需求少
参数的更新不受梯度的伸缩变换影响
超参数具有很好的解释性，且通常无需调整或仅需很少的微调
更新的步长能够被限制在大致的范围内（初始学习率）
能自然地实现步长退火过程（自动调整学习率）
很适合应用于大规模的数据及参数的场景
适用于不稳定目标函数
适用于梯度稀疏或梯度存在很大噪声的问题

代码实现

根据公式我们可以得到下面的代码

class Adam:
    """Adam优化器
    """
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
    
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)        
        self.iter += 1
        
        for key in params.keys():
            self.m[key] = self.beta1 * self.m[key] + (1 - self.beta1) * grads[key]
            self.v[key] = self.beta2 * self.v[key] + (1 - self.beta2) * (grads[key]**2)
            m_hat = self.m[key] / (1 - self.beta1**self.iter)
            v_hat = self.v[key] / (1 - self.beta2**self.iter)
            params[key] -= self.lr * m_hat / (np.sqrt(v_hat) + 1e-7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

为了将上面的代码和前面的Momentum、AdaGrad、RMSProp等算法的形式保持一致，我们还可以将代码进行优化写成下面的形式：

class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)        # 先对系数进行计算 
        
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])          
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

上面代码中的lr_t是对 $\alpha$ 、 $\hat{m_{t}}$ 、 $\hat{v_{t}}$ 先进行了提前计算，我们将下面两个公式

$\hat{m_{t}} = \frac{m_{t}}{1-\beta _{1}^{t}}$
$\hat{v_{t}} = \frac{v_{t}}{1-\beta _{2}^{t}}$
代入到
$\alpha \cdot \frac{\hat{m_{t}}}{(\sqrt{\hat{v_{t}}} + \varepsilon )}$
得到
$\alpha \cdot \frac{\frac{m_{t}}{1-\beta_{1}^{t} } }{(\sqrt{\frac{v_{t}}{1-\beta_{2}^{t} }} + \varepsilon )}$
将分子分母同乘以 $\sqrt{1-\beta_{2}^{t}}$ ,得到：
$\alpha \cdot \frac{\frac{\sqrt{1-\beta_{2}^{t}}}{1-\beta_{1}^{t} } m_{t} }{\sqrt{v_{t}} + \varepsilon}$

由于 $\alpha$ 、 $\beta_{1}$ 、 $\beta_{2}$ 均为常数项，所以可以先行计算，除了看起来形式更加简单，并且减少了矩阵运算，因此得到了：

     lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)    
1

上述代码中的：

self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])  
1
2

拆开后与最原始的代码是一样的，好处就是看起来更规整

self.m[key] = self.beta1 * self.m[key] + (1 - self.beta1) * grads[key]
 self.v[key] = self.beta2 * self.v[key] + (1 - self.beta2) * (grads[key]**2)
1
2

实例演示

通过以上的优化器来求解下面公式的最小值

$\frac{1}{20}x^2 + y^2$

该函数的图形如下左图所示和它的等高线如右图所示
在这里插入图片描述

代码

import sys
import os
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


class SGD:
    """
    SGD
    """
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key] 


class Momentum:
    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]


class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]


class AdaGrad:
    """AdaGrad算法
    """

    def __init__(self, lr=0.01) -> None:
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            # 防止除数为0，加上1e-7
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:

    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

def f(x, y):
    return x**2 / 20.0 + y**2


def df(x, y):
    return x / 10.0, 2.0*y


def main():
    init_pos = (-7.0, 2.0)
    grads = {'x': 0, 'y': 0}

    optimizers = OrderedDict()
    optimizers['SGD'] = SGD(lr=0.95)
    optimizers["Momentum"] = Momentum(lr=0.1)
    optimizers["Nesterov"] = Nesterov(lr=0.1)
    optimizers["AdaGrad"] = AdaGrad(lr=0.5)
    optimizers["RMSprop"] = RMSprop(lr=0.1)
    optimizers["Adam"] = Adam(lr=0.1)

    idx = 1
    for key in optimizers:
        print(key)
        optimizer = optimizers[key]
        x_history = []
        y_history = []
        params = {'x': init_pos[0], 'y': init_pos[1]}

        for i in range(300):
            x_history.append(params['x'])
            y_history.append(params['y'])

            grads['x'], grads['y'] = df(params['x'], params['y'])
            optimizer.update(params, grads)

        x = np.arange(-10, 10, 0.01)
        y = np.arange(-5, 5, 0.01)

        X, Y = np.meshgrid(x, y)
        Z = f(X, Y)
        # for simple contour line
        mask = Z > 7
        Z[mask] = 0

        # plot
#         plt.figure(figsize=(100,200))
#         plt.subplot(3, 2, idx)
        idx += 1
        plt.plot(x_history, y_history, 'o-', color="red")
        plt.contour(X, Y, Z)
        plt.ylim(-10, 10)
        plt.xlim(-10, 10)
        plt.plot(0, 0, '+')
        # colorbar()
        # spring()
        plt.title(key)
        plt.xlabel("x")
        plt.ylabel("y")
        plt.show()

if __name__ == '__main__':
    main()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189

输出结果

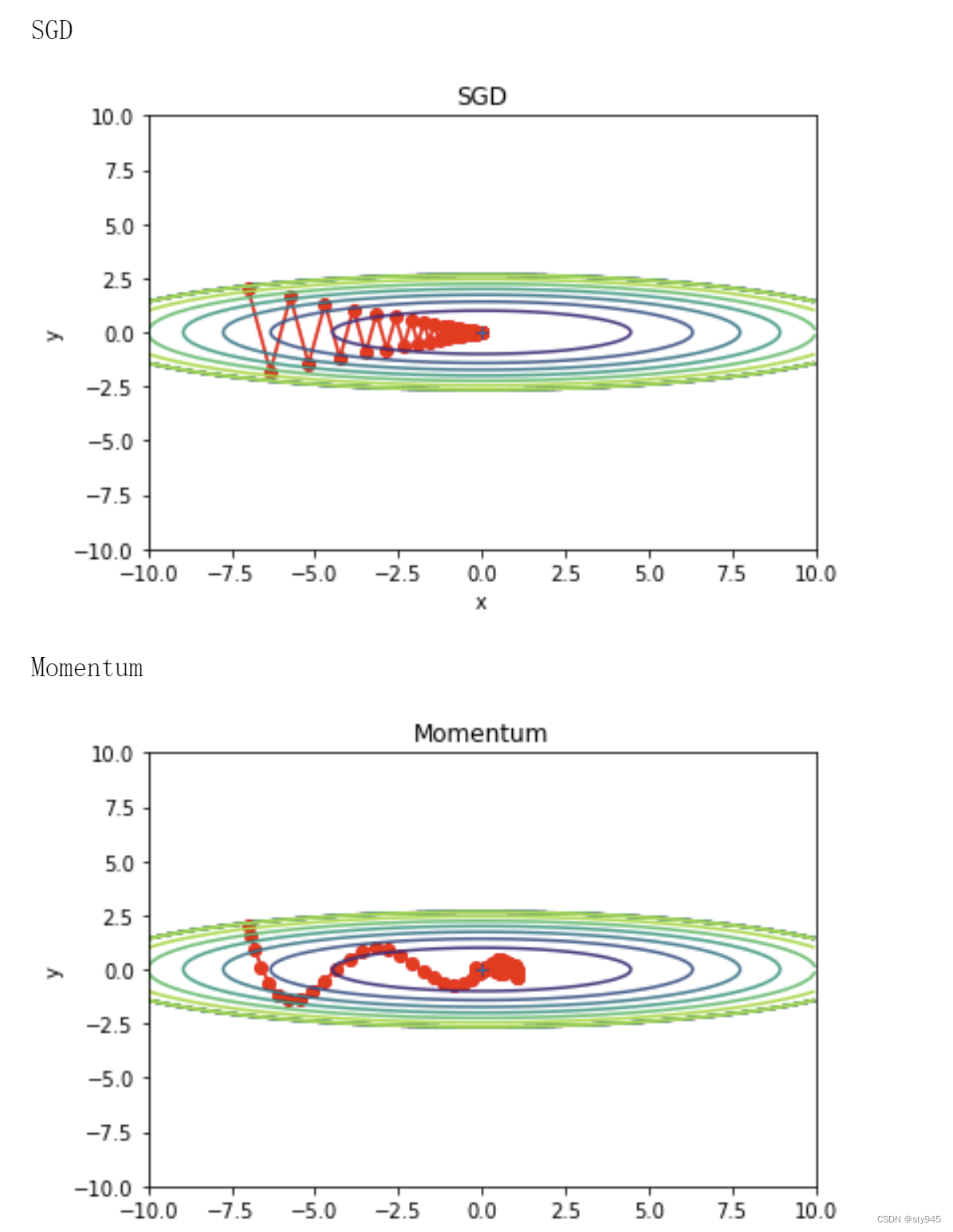
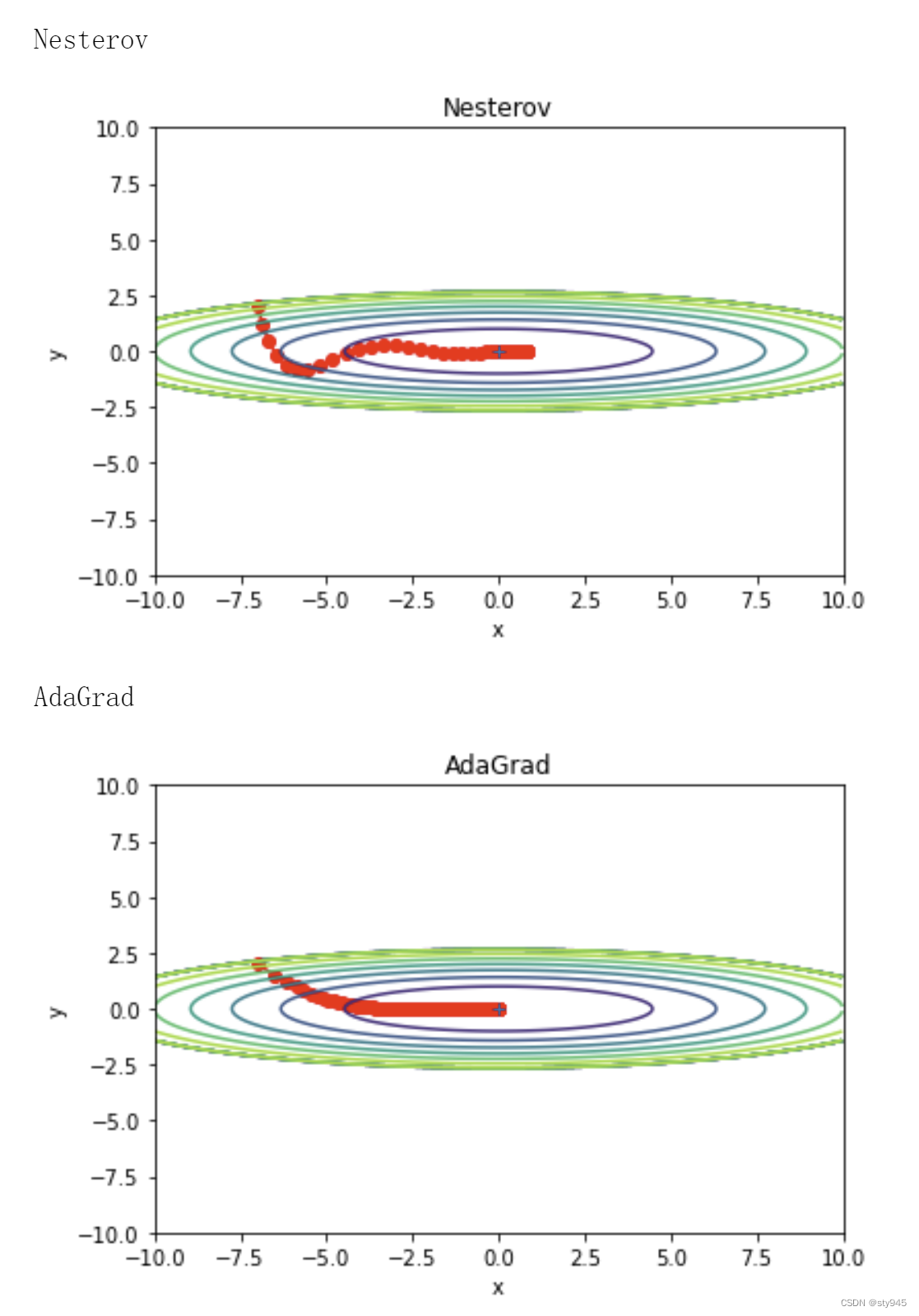
在这里插入图片描述

最后

通过对优化器的细节进行一番了解，收获良多，但是还是有很多需要学习的地方，比如优化器中的参数如何设置比较合适、什么情况该选择怎样的优化器，这些都是需要认真考虑的地方。

希望上述知识也能对大家有所帮助，如果觉得不错，可以点赞支持。

如果有不足之处，欢迎评论区进行交流

参考

详解随机梯度下降法（Stochastic Gradient Descent，SGD）通俗形象的解释
随机梯度下降SGD算法理解
 Nesterov加速和Momentum动量方法
 ADVANCES IN OPTIMIZING RECURRENT NETWORKS
从 SGD 到 Adam —— 深度学习优化算法概览(一)
cs231 First-order (SGD), momentum, Nesterov momentum
关于深度学习的优化器选择
 TensorFlow momentum SGD实现
 Deep Learning 之最优化方法
 优化器(Optimizer)（SGD、Momentum、AdaGrad、RMSProp、Adam）包含pytorch引用
An overview of gradient descent optimization algorithms
Practical Recommendations for Gradient-Based Training of Deep Architectures from Yoshua Bengio

相关阅读:
C++ 多态
Android 左右滑屏，实现Back按键
docker启动已存在容器
专车数据层架构进化往事：好的架构是进化来的，不是设计来的
GEE错误——Image.select: Pattern ‘MDF‘ did not match any bands
Flink部署——细粒度资源管理
打家劫舍3(二叉树型)Java
C++ Reference: Standard C++ Library reference: C Library: cwchar: wcscmp
Assertion介绍
学习Java基础面试题第五天

原文地址：https://blog.csdn.net/sty945/article/details/125975665