王道数据结构【二叉树】部分代码实现（C语言）

在顺序存储的二叉树中寻找两个节点的最近公共祖先

//sequenceTree.cpp
/*
	采用顺序存储保存一个二叉树，我们要将一个普通的树转换成一颗完全二叉树，将不存在的节点用9999代替
*/
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
void createBiTree(int *arr,int count) {
	int i = 1,data;
	//int *arr = (int *)malloc(sizeof(int)*(count+2));//下标为0我们不存，最后要有结束标识符
	while (count--) {
		printf("请输入第%d个节点:",i);
		scanf("%d",&data);
		*(arr + i) = data;
		i++;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

/*
	已知一课二叉树按顺序存储结构进行存储，设计一个算法，求编号分别为i和j的两个节点的最近的公共祖先节点的值
	分析：
		利用数组存储一颗二叉树，一般来说我们用这种方式存储一颗完全二叉树，不浪费空间
*/
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
int findCommonAncestor(int *arr,int i,int j) {
	while (i!=j) {
		i > j ? i = i / 2: j = j / 2;
	}
	return *(arr + i);
}
int main() {
	void createBiTree(int *,int);
	int count,i,j;
	printf("请输入所要创建的二叉树，其转换为完全二叉树的最少节点数：count=");
	scanf("%d",&count);
	int *arr = (int *)malloc(sizeof(int)*(count + 2));//下标为0我们不存
	createBiTree(arr,count);
	printf("请输入要查找公共节点的两个节点的编号,编号<=%d:\n",count);
	printf("i=");
	scanf("%d",&i);
	printf("\n");
	printf("j=");
	scanf("%d", &j);
	while (i>count || j>count || *(arr+i)==9999||*(arr+j)==9999 ){
		printf("编号有误，请重新输入：\n");
		printf("i=");
		scanf("%d", &i);
		printf("\n");
		printf("j=");
		scanf("%d", &j);
	}
	count = findCommonAncestor(arr,i,j);
	printf("公共祖先的值为:%d",count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

中序非递归遍历

/*
	是写出中序遍历的非递归算法
	分析：
		如果采用非递归，我们就需要用到栈这个数据结构了，具体流程为：从根节点一路往下找左孩子并将其入栈直至左孩子为空
		然后依次出栈，并判断是否存在右孩子，如果有，右孩子入栈，继续往下找左孩子，如此重复直至栈空
*/
struct biTree {//树的结构体
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {//栈的结构体
	char* arr;	//内存首地址
	int  len;	//栈的容量
	int top; 	//栈的下标
};
#include 
#include 
void inOrder(biTree *T,Stack *s) {//中序遍历
	biTree *p = T;
	bool empty(Stack *);
	bool push(Stack *,biTree * );
	biTree *top(Stack *);
	bool pop(Stack *);
	while (p||!empty(s)) {
		if (p) {//一路向左
			push(s,p);
			p = p->lchild;
		}
		else {
			p = top(s);
			printf("%c ",p->data);//打印栈顶元素
			pop(s);//栈顶元素出栈
			p = p->rchild;//向右寻找
		}
	}
}
int main() {
	int count=0;//计数器，二叉树节点个数
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Stack *s = (struct Stack*)malloc(sizeof(struct Stack));
	biTree *create(biTree*);
	void nodeNum(biTree *,int *);
	Stack *createStack(int);

	T = create(T);
	nodeNum(T,&count);

	s = createStack(count);//创建二叉树节点个数大小的栈

	inOrder(T,s);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

先序非递归遍历

/*
	试写出先序遍历（非递归算法）
	分析：
		和中序遍历大同小异，唯一的差别在于每次先访问节点，在判断有没有左孩子，有则入栈，然后出栈，往右走。直至栈空。
*/
struct biTree {//树的结构体
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {//栈的结构体
	char* arr;	//内存首地址
	int  len;	//栈的容量
	int top; 	//栈的下标
};
#include 
#include 
void preOrder(biTree *T, Stack *s) {//先序遍历
	biTree *p = T;
	bool empty(Stack *);
	bool push(Stack *, biTree *);
	biTree *top(Stack *);
	bool pop(Stack *);
	while (p || !empty(s)) {
		if (p) {//一路向左
			printf("%c ", p->data);//打印当前元素
			push(s, p);
			p = p->lchild;
		}
		else {
			p = top(s);
			pop(s);//栈顶元素出栈
			p = p->rchild;//向右寻找
		}
	}
}
int main() {
	int count = 0;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Stack *s = (struct Stack*)malloc(sizeof(struct Stack));
	biTree *create(biTree*);
	void nodeNum(biTree *, int *);
	Stack *createStack(int);

	T = create(T);
	nodeNum(T, &count);

	s = createStack(count);//创建二叉树节点个数大小的栈

	preOrder(T, s);
	return 0;
}
//一名谦虚的学生
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

后序非递归遍历

/*
	试写出非递归的后序遍历算法
	分析：
		非递归的后续遍历较中序和先序而言，稍微复杂一点，首先我们需要一直从根节点往下寻找左孩子并入栈，之后访问栈顶元素，
		并判断是否有右孩子，如果有右孩子入栈，并继续往左孩子找，直到某节点为单节点，出栈并访问。需要注意的是因为有可能一个节点我们
		会访问多次，所以我们设置一个指针r用来表示上一次被访问过得节点



*/
struct biTree {//树的结构体
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {//栈的结构体
	biTree** arr;	//内存首地址
	int  len;	//栈的容量
	int top; 	//栈的下标
};
#include 
#include 
void postOrder(biTree *T, Stack *s) {//后序遍历
	biTree *p = T;
	biTree *r = (struct biTree*)malloc(sizeof(struct biTree));
	bool empty(Stack *);
	bool push(Stack *, biTree *);
	biTree *top(Stack *);
	bool pop(Stack *);
	while (p || !empty(s)) {
		if (p) {//一路向左
			push(s, p);
			p = p->lchild;
		}
		else {
			p = top(s);
			if (p->rchild&&r != p->rchild) {
				p = p->rchild;
				push(s, p);
				p = p->lchild;
			}
			else {
				printf("%c ", p->data);//打印栈顶元素
				r = p;
				pop(s);//栈顶元素出栈
				p = NULL;//这里一定要将p设为NULL，因为p的孩子已经遍历过了，不设置为NUll的话，又会将左孩子压入栈
			}

		}
	}
}
int main() {
	int count = 0;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Stack *s = (struct Stack*)malloc(sizeof(struct Stack));
	biTree *create(biTree*);
	void nodeNum(biTree *, int *);
	Stack *createStack(int);

	T = create(T);
	nodeNum(T, &count);

	s = createStack(count);//创建二叉树节点个数大小的栈

	postOrder(T, s);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

层序遍历

/*
	试写出层次遍历的算法
	分析：
		正如名字所表现的那样，要一层一层的遍历，这里我们就需要用到队列这种数据结构了，具体做法是：
		先将根节点入队，然后根节点出队，并依次将根节点的左孩子、右孩子入队。后续如此循环，直至队空
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Squeue {
	biTree *arr;
	int front, rear;
};
#include 
#include 
void levelOrder(biTree *T,Squeue *sq,int maxSize) {
	struct biTree *p = T;
	struct biTree *r = (struct biTree *)malloc(sizeof(struct biTree));
	bool enQueueS(Squeue *, biTree *, int);
	bool isEmpty(Squeue *);
	bool deQueueS(Squeue *, biTree *,int);
	enQueueS(sq,p,maxSize);
	while (!isEmpty(sq)) {
		deQueueS(sq,r,maxSize);
		printf("%c ",r->data);
		if(r->lchild)enQueueS(sq, r->lchild, maxSize);
		if (r->rchild)enQueueS(sq, r->rchild, maxSize);
	}
}
int main() {
	int count = 0;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Squeue *sq = (struct Squeue *)malloc(sizeof(struct Squeue));

	biTree *create(biTree *);
	void nodeNum(biTree *,int *);

	Squeue *createQueue(int);
	T = create(T);//创建一颗二叉树
	nodeNum(T,&count);//统计二叉树节点个数
	sq = createQueue(count);

	levelOrder(T,sq,count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

构建线索二叉树

/*
	该文件用于创建三类线索二叉树，即中序线索二叉树、先序线索二叉树、后序线索二叉树
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
	int ltag, rtag;//用于进行标记
};
#include 

void inThread(biTree *p, biTree *pre ) {//中序线索二叉树
	if (p!=NULL) {
		inThread(p->lchild,pre);
		if (p->lchild==NULL) {//如果左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if (pre!=NULL && pre->rchild==NULL) {//建立前驱结点的后继线索
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;
		inThread(p->rchild,pre);
	}
}
void preThread(biTree *p, biTree *pre) {//先序线索二叉树
	if (p != NULL) {

		if (p->lchild == NULL) {//如果左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if (pre != NULL && pre->rchild == NULL) {//建立前驱结点的后继线索
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;
		inThread(p->lchild, pre);
		inThread(p->rchild, pre);
	}
}
void postThread(biTree *p, biTree *pre) {//后序线索二叉树
	if (p != NULL) {
		inThread(p->lchild, pre);
		inThread(p->rchild, pre);
		if (p->lchild == NULL) {//如果左子树为空，建立前驱线索
			p->lchild = pre;
			p->ltag = 1;
		}
		if (pre != NULL && pre->rchild == NULL) {//建立前驱结点的后继线索
			pre->rchild = p;
			pre->rtag = 1;
		}
		pre = p;
		
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

自下而上，从右到左的层次遍历

/*
	试给出二叉树的自下而上、从右到左的层次遍历算法
	分析：
		我们只需要在层次遍历的基础上加入栈的使用，我们每次出队后的数据将其入栈，队列空了时，再去依次访问栈中元素，即可达到要求

*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Squeue {
	biTree *arr;
	int front, rear;
};
struct Stack {
	biTree *arr;
	int len;
	int top;
};
#include 
#include 
void levelOrder2(biTree *T, Squeue *sq, int maxSize) {
	struct Stack *s = (struct Stack *)malloc(sizeof(struct Stack));
	struct biTree *p = T;
	struct biTree *r = (struct biTree *)malloc(sizeof(struct biTree));
	bool enQueue(Squeue *, biTree *, int);
	bool isEmpty(Squeue *);
	bool deQueue(Squeue *, biTree **, int);

	Stack *createStack(int);
	bool push(Stack *,biTree *);
	bool empty(Stack *);
	biTree *top(Stack *);
	bool pop(Stack *);

	s = createStack(maxSize);
	enQueue(sq, p, maxSize);
	while (!isEmpty(sq)) {
		deQueue(sq, &r, maxSize);
		push(s,r);
		if (r->lchild)enQueue(sq, r->lchild, maxSize);
		if (r->rchild)enQueue(sq, r->rchild, maxSize);
	}
	while (!empty(s)) {
		r = top(s);
		printf("%c ",r->data);
		pop(s);
	}

}
int main() {
	int count = 0;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Squeue *sq = (struct Squeue *)malloc(sizeof(struct Squeue));

	biTree *create(biTree *);
	void nodeNum(biTree *, int *);

	Squeue *createQueue(int);
	T = create(T);//创建一颗二叉树
	nodeNum(T, &count);//统计二叉树节点个数
	sq = createQueue(count);

	levelOrder2(T, sq, count);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

非递归算法求解二叉树高度

/*
	假设二叉树采用二叉链表存储结构，设计一个非递归算法求二叉树的高度
	分析：
		若要采用非递归的方式来求得二叉树的高度，我们采用层次遍历是最合适的，因为这一层一层的不就很好数吗哈哈。具体实现：
		这里唯一的难点就在于我们如何得知高度该加一了；我们可以设置一个标志num用来记录每一层入栈的节点个数，当我们出栈数
		达到该数值时也就意味着我们的高度该加一了
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Squeue {
	biTree *arr;
	int front, rear;
};

#include 
#include 

int getHigh(biTree *T,Squeue *sq,int maxSize) {
	int oldNum=0,curNum=0,high=0;//记录一层有多少节点
	struct biTree *p = T;
	struct biTree *r=(struct biTree *)malloc(sizeof(struct biTree));
	bool enQueue(Squeue *, biTree *, int );
	bool isEmpty(Squeue *);
	bool deQueue(Squeue *, biTree **, int);

	enQueue(sq,p,maxSize);//将根节点入队
	oldNum++;//此时队列中只有一个节点

	while (!isEmpty(sq)) {
		deQueue(sq,&r,maxSize);//取出队首元素
		if (r->lchild) {
			curNum++;//下一层的节点数+1
			enQueue(sq, r->lchild, maxSize);//将节点入队
		}
		if (r->rchild) {
			curNum++;//下一层的节点数+1
			enQueue(sq, r->rchild, maxSize);//将节点入队
		}
		if (!--oldNum) {//如果一层的元素已取完，高度+1
			high++;
			oldNum = curNum;//当oldNum=0时，将下一层的节点数赋给它
			curNum = 0;//下一层节点归零
		}
		
	}
	return high;
}
int main() {
	int count=0;
	//创建二叉树、队列
	struct biTree *T=(struct biTree *)malloc(sizeof(struct biTree));
	struct Squeue *sq;
	biTree *create(biTree *);
	void nodeNum(biTree *,int *);
	Squeue *createQueue(int);
	T = create(T);
	nodeNum(T,&count);
	sq = createQueue(count);//创建一个大小为树节点个数的队列

	printf("该二叉树的高度为：%d",getHigh(T, sq, count));
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

根据先序和后序序列求解二叉树

/*
	设一个二叉树各节点的值互不相同，其先序遍历序列和中序遍历序列分别存于两个一维数组A、B中，试编写算法建立该二叉树的二叉链表
	分析：
		这是一个典型的已知中序和先序求二叉树的案例，具体实现步骤如下：
		1、先根据先序序列确定树的根节点
		2、根据根节点在中序在中序序列中划分出二叉树的左右子树包含哪些节点，然后根据左右子树节点在先序序列中的次序确定子树的
		的根节点，即回到步骤一。
		如此重复，直到每颗子树仅有一个节点为止
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#include 
#include 
biTree *preInCreate(char *arrIn,char *arrPre,int l1,int h1,int l2,int h2) {
	//l1 h1 为中序的第一和最后一个节点下标，l2 h2 为先序的第一和最后一个节点下标
	int llen, rlen,i;//左子树、右子树长度
	struct biTree *root = (struct biTree *)malloc(sizeof(struct biTree));
	root->data = *(arrPre + l2);
	for (i = l1; *(arrIn + i) != root->data; i++);//找到根节点在中序序列的位置
	
	llen = i - l1;//记录左边节点个数
	rlen = h1 - i;//记录根节点右边节点个数
	if (llen) {
		root->lchild = preInCreate(arrIn,arrPre,l1,l1+llen-1,l2+1,l2+llen);//把左边的序列有看做一个新的继续找根节点
	}
	else {
		root->lchild = NULL;
	}
	if (rlen) {
		root->rchild = preInCreate(arrIn, arrPre, h1-llen+1, h1, h2-llen+1, h2);//把右边的序列有看做一个新的继续找根节点
	}
	else {
		root->rchild = NULL;
	}
	return root;
}
int main() {
	char arrIn[] = { 'D','B','E','A','F','C','G' }, 
		arrPre[] = {'A','B','D','E','C','F','G'};
	struct biTree *root;
	void inOrder(biTree *);
	void preOrder(biTree *);
	root = preInCreate(arrIn,arrPre,0,6,0,6);
	inOrder(root);
	printf("\n");
	preOrder(root);

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

判断一颗树是否是完全二叉树

/*
	一颗二叉树以二叉链表的形式存储，编写一个算法判断其是否是一个完全二叉树
	分析：
		我们仍然可以借助队列来完成这件事，具体做法为：我们依次将二叉树从上到下，从左到右入栈，包括空节点，如遇空节点，
		若队列非空，则判断其后是否还存在节点，若有，则该树为非完全二叉树。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Squeue {
	biTree data;
	int front, rear;
};
#include 
#include 
bool isComplete(biTree *T, Squeue *sq, int maxSize) {
	if (!T)return true;
	bool enQueue(Squeue *, biTree *, int maxSize);
	bool deQueue(Squeue *, biTree **, int maxSize);
	bool isEmpty(Squeue *);
	struct biTree *p = T;
	struct biTree *r = (struct biTree*)malloc(sizeof(struct biTree));
	enQueue(sq, p, maxSize);//根节点入队
	while (!isEmpty(sq)) {
		deQueue(sq, &r, maxSize);//取出队首元素
		if (r) {
			enQueue(sq, r->lchild, maxSize);
			enQueue(sq, r->rchild, maxSize);
		}
		else {
			while (!isEmpty(sq)) {//如果已经来到了空节点，判断后续是否还有节点
				deQueue(sq, &r, maxSize);//取出队首元素
				if (r) {
					return false;
				}
			}
		}
	}
	return true;
}
int main() {
	int count = 0;
	bool isCom;
	struct biTree *T = (struct biTree*)malloc(sizeof(struct biTree));
	struct Squeue *sq;

	biTree *create(biTree *);
	void nodeNum(biTree *, int *);

	Squeue *createQueue(int);


	T = create(T);//创建一颗二叉树
	nodeNum(T, &count);//统计二叉树节点数量
	sq = createQueue(count);//创建容量为二叉树节点个数大小的队列

	isCom = isComplete(T, sq, count);
	isCom ? printf("该二叉树是完全二叉树") : printf("该二叉树不是完全二叉树");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

统计双分支节点个数

/*
	假设二叉树采取二叉链表存储结构存储，试设计一个算法，计算一颗给定的二叉树所有的双分支节点个数
	分析：
		其实二叉树各类操作都十分适合递归，这里我们同样可以采取递归的做法来进行统计双分支节点的个数。具体做法，我们
		最开始便定义一个静态变量，递归出口既是无左右孩子。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#include 
#include 
int doubleNode(biTree *T) {
	static int num = 0;//注意这里一定要使用静态变量，不然每一次进入递归都会初始化num
	if (!T)num = 0;
	if (T->lchild&&T->rchild) {
		num++;
		doubleNode(T->lchild);
		doubleNode(T->rchild);
	}
	else {
		if (T->lchild)doubleNode(T->lchild);
		if (T->rchild)doubleNode(T->rchild);
	}
	return num;
}
int main() {
	int num;
	struct biTree *T = (struct biTree*)malloc(sizeof(struct biTree));
	biTree *create(biTree *);
	T = create(T);//创建一颗二叉树
	num = doubleNode(T);
	printf("该二叉树中的双分支节点个数有：%d",num);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

交换左右子树

/*
	试编写一个算法将一颗二叉树的所有节点的左右子树进行交换。
	分析：
		我们仍然可以采用递归的方式进行交换
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#include 
#include 
void swapTree(biTree *T) {//其本质就是从叶子节点开始进行交换，一路推进到根节点
	struct biTree *p = T,*t;
	if (!p) return;
	if (!p->lchild&&!p->rchild) {//如果没有左右孩子，就不需要交换了，直接返回
		return;
	}
	else {
		swapTree(p->lchild);//交换左子树
		t = p->lchild;
		p->lchild = p->rchild;
		p->rchild = t;
		swapTree(p->rchild);//交换右子树
	}
}
int main() {
	int num;
	struct biTree *T = (struct biTree*)malloc(sizeof(struct biTree));
	biTree *create(biTree *);
	void inOrder(biTree *);
	T = create(T);//创建一颗二叉树
	inOrder(T);
	printf("\n");
	swapTree(T);
	inOrder(T);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

寻找先序遍历第k个节点

/*
	假设二叉树是用二叉链表存储，试设计一个算法,求先序遍历中第k（1<=k<=二叉树的节点个数）个节点的值
	分析：
		很简单，每遍历一个节点，计数器便加一，直至等于k
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
biTree *preK(biTree *T, int k) {
	static int num = 0;
	static biTree *r;
	if (!T) return NULL;
	if (++num == k) {//找到后，记录下来
		r = T;
	}
	else {
		preK(T->lchild, k);
		preK(T->rchild, k);
	}

	return r;
}
int main() {
	int k, count = 0;
	struct biTree *T = (struct biTree*)malloc(sizeof(struct biTree));
	T->lchild = NULL;
	T->rchild = NULL;
	T->data = NULL;
	struct biTree *r;
	biTree *create(biTree *);
	void inOrder(biTree *);
	void nodeNum(biTree *, int *);
	T = create(T);//创建一颗二叉树
	nodeNum(T, &count);
	if (!count) {
		printf("该二叉树是空树");
	}
	else {
		printf("请输入要寻找的k值（1<=k<=%d）：k=", count);
		scanf("%d", &k);
		while (k<1 || k>count) {
			printf("输入有误，请重输 k=");
			scanf("%d", &k);
		}
		r = preK(T, k);
		printf("第%d个节点值为%c", k, r->data);
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

删除以x为值的节点的子树

/*
	已知二叉树以二叉链表存储，编写算法完成：对于树中每一个元素值为x的结点，删除以它为根的子树，并释放相应的空间
	分析：
		因为我们要删除以寻找到的元素为根的子树，所以我们删除时应采用递归后序遍历进行删除释放，寻找x采用先序遍历
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
void del(biTree *T) {//释放结点函数
	if (T) {
		if (T->lchild)del(T->lchild);
		if (T->rchild)del(T->rchild);
		free(T);
	}

}
void delXsub(biTree *T, int x) {//这里设置一个父节点指针，因为free只会释放所在节点里面的内容，并不会置空
	struct biTree *p = T;
	if (p->lchild && p->lchild->data == x) {
		del(p->lchild);
		p->lchild = NULL;
	}
	if (p->rchild && p->rchild->data == x) {
		del(p->rchild);
		p->rchild = NULL;
	}
	if (p->lchild) delXsub(p->lchild, x);
	if (p->rchild) delXsub(p->rchild, x);


}
int main() {
	char x;
	struct biTree *T = (struct biTree*)malloc(sizeof(struct biTree));
	biTree *create(biTree *);
	void inOrder(biTree *);
	T = create(T);//创建一颗二叉树
	printf("请输入要寻找的x值：x=");
	scanf("%c", &x);
	if (T->data == x) {
		del(T);
	}
	else {
		delXsub(T, x);
	}
	inOrder(T);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

寻找值为x的节点的所有祖先

/*
	在二叉树中查找值为x的节点，试编写算法打印值为x的节点的所有祖先，假设x的值不多于一个。
	分析：
		这里我们采用后序遍历（非递归），因为在我们遇到x之前我们会把它的祖先节点全部入栈，当我们找到x时，再依次取出栈中元素
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {
	biTree *arr;
	int len;
	int top;
};
#include 
#include 
void findAllAncestor(biTree *T, Stack *s, char x) {
	struct biTree *p = T;
	struct biTree *r = (struct biTree *)malloc(sizeof(struct biTree));
	struct biTree *tp = (struct biTree *)malloc(sizeof(struct biTree));

	bool push(Stack *, biTree*);
	bool pop(Stack *);
	biTree *top(Stack *);//返回得是一个指针
	bool empty(Stack *);
	while (p || !empty(s)) {
		if (p) {//一路将所有左孩子入栈
			push(s, p);
			p = p->lchild;
		}
		else {//没有左孩子，
			p = top(s);
			if (p->rchild && p != r) {//将右子树的所有左孩子入栈
				r = p;
				p = p->rchild;
			}
			else {//当既没有左孩子也没有右孩子时，该出栈了
				pop(s);//被查找元素先出栈
				if (p->data == x) {//找到了，那么如果栈中有元素，那全都是它的祖先
					printf("祖先元素有:");
					while (!empty(s)) {
						tp = top(s);
						printf("%c ", tp->data);
						pop(s);
					}

				}
				p = NULL;//一定要将p置空，不然又会把p的左孩子入栈
			}
		}


	}
}
int main() {
	int count = 0, x;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	struct Stack *s;

	biTree *create(biTree *);
	void nodeNum(biTree *, int *);

	Stack *createStack(int);

	T = create(T);
	nodeNum(T, &count);
	s = createStack(count);
	printf("请输入要查找的元素：x=");
	x = getchar();
	findAllAncestor(T, s, x);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

寻找最近公共祖先

/*
	p、q分别为指向该二叉树中任意两个节点的指针，试编写算法ancestor(root,p,q,r),找到p、q的最近公共祖先节点r
	分析：
		上一道题其实可以给我们一些启示，就是我们可以将任意节点的祖先存起来，那这里我们也可以用两个栈，分别将p、q
		的祖先存在栈中，因为栈顶是最近的祖先节点，所以我们可以一次往下寻找相同节点，第一次找到的相同节点便是最近公共
		祖先节点。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {
	biTree *arr;
	int len;
	int top;
};
#include 
#include 
void findAncestor(Stack *s, biTree *m, biTree *x) {
	struct biTree *r = (struct biTree *)malloc(sizeof(struct biTree));
	bool empty(Stack *);
	bool push(Stack *, biTree*);
	bool pop(Stack *);
	biTree *top(Stack *);//返回得是一个指针
	
	while (m || !empty(s)) {
		if (m) {//一路将所有左孩子入栈
			push(s, m);
			m = m->lchild;
		}
		else {//没有左孩子，
			m = top(s);
			if (m->rchild&&r != m->rchild) {
				m = m->rchild;
				push(s, m);
				m = m->lchild;
			}
			else {//当既没有左孩子也没有右孩子时，该出栈了
				pop(s);//被查找元素先出栈
				if (m->data == x->data) {//找到了，那么如果栈中有元素，那全都是它的祖先
					break;
				}
				r = m;
				m = NULL;//一定要将p置空，不然又会把m的左孩子入栈
			}
		}
	}
}
void findNearestAncestor(biTree *T, biTree *p, biTree *q, biTree **r) {
	int count = 0;
	struct biTree *m = T;//另起指针m，指向根节点
	void nodeNum(biTree *, int *);
	nodeNum(T, &count);//统计节点个数
	struct Stack *sp, *sq;
	Stack *createStack(int);
	sp = createStack(count);
	sq = createStack(count);

	
	findAncestor(sp, m, p);//寻找p节点的祖先,放到栈中
	findAncestor(sq, m, q);//寻找q节点的祖先

	//经过上面的操作，栈sp和sq里面已经存好了p、q各自的祖先，接下来便是寻找最近祖先
	bool contain(Stack *,biTree *);
	bool empty(Stack *);
	bool push(Stack *, biTree*);
	bool pop(Stack *);
	biTree *top(Stack *);//返回得是一个指针
	while (!empty(sp)) {//当sp不空
		*r = top(sp);
		if (contain(sq,*r)) {//判断sq中知否包含d
			break;
		}
		pop(sp);
	}
}
int main() {
	int count = 0;
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree)), *p, *q;
	struct biTree *r = (struct biTree *)malloc(sizeof(struct biTree));
	biTree *create(biTree *);

	T = create(T);
	p = T->lchild->lchild->rchild;//手动指定一个节点，切记不要指成NULL了
	q = T->rchild->rchild;
	//p = T->lchild;
	//q = T->rchild;
	findNearestAncestor(T, p, q, &r);//记得这里要将r的地址传过去，才能进行改变
	printf("p q最近公共结点为值为：%c",r->data);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

求二叉树宽度

/*
	假设二叉树采用二叉链表存储结构，设计一个算法，求非空二叉树的宽度（即具有节点数最多的那一层的节点个数）
	分析：
		这道题和求高度那道题大同小异。我们仍然可以采取层次遍历，统计每一层的节点个数，找到宽度最大的那一层。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;

};
struct LinkQueue {//上次求高度采用的是顺序队列，这次采用链式队列，雨露均沾哈哈
	struct Link *front, *rear;
};

#include 
#include 

int getWidth(biTree *b, LinkQueue *lq) {
	int oldNum = 0, curNum = 0, width = 0;;
	bool enQueue(LinkQueue *lq, biTree *node);
	bool deQueue(LinkQueue *lq, biTree **node);
	bool isEmpty(LinkQueue *lq);
	struct biTree *p = b;
	struct biTree *r=(struct biTree*)malloc(sizeof(struct biTree));
	if (p) {
		enQueue(lq, p);//入队
		oldNum++;
		width = 1;
		while (!isEmpty(lq)) {
			while (oldNum--) {
				deQueue(lq, &r);//队首元素出队
				if (r->lchild) {//若有左孩子，将左孩子入队
					enQueue(lq, r->lchild);
					curNum++;//当前队列元素加1
				}
				if (r->rchild) {//若有右孩子，将右孩子入队
					enQueue(lq, r->rchild);
					curNum++;//当前队列元素加1
				}
			}
			curNum > width ? width = curNum : NULL;//如果当前队列元素多于之前的，宽度变更
			oldNum = curNum;//继续进行操作
			curNum = 0;

		}

	}
	return width;
}
int main() {
	struct biTree *b = (struct biTree*)malloc(sizeof(struct biTree));
	struct LinkQueue *lq;

	biTree *create(biTree *);
	b = create(b);//创建一颗二叉树

	LinkQueue *create();
	lq = create();//创建链式队列

	printf("该二叉树的宽度为：%d",getWidth(b, lq));
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

preToPost

/*
	设有一颗满二叉树（所有节点值均不同），已知其先序序列为pre，设计一个算法求其后序序列post
	分析：
		题目已经告诉我们是一颗满二叉树，那我们就可以从先序序列推出后序序列，因为满二叉树总是对半分的，具体操作：
		1、找出先序序列的根节点，将其放入后序序列数组末尾；
		2、将根节点之后的节点分成左右两堆，在分别执行上一步
		3、直至全部处理完
*/

#include 

void preToPost(char *arrPre,char *arrPost,int l1,int h1,int l2,int h2) {
	//l1,h1,l2,h2代表arrPre和arrPost的起点和末尾
	int half;
	if (l1 <= h1) {
		half = (h1 - l1) / 2;
		*(arrPost + h2) = *(arrPre + l1);
		preToPost(arrPre, arrPost, l1 + 1, l1 + half, l2, l2 + half - 1);//左边
		preToPost(arrPre, arrPost, l1 + half + 1, h1, l2+ half, h2-1);//右边
	}

}
int main() {
	char arrPre[] = {'A','B','D','M','C','F','G'},arrPost[7];
	preToPost(arrPre,arrPost,0,6,0,6);
	for (int i = 0; i < 7;i++) {
		printf("%c ",*(arrPost+i));
	}
	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

单链表连接叶节点

/*
	设计一个算法将二叉树的叶节点按从左到右的顺序连成一个单链表，表头指针为head。二叉树按二叉链表方式存储，连接时用叶节点的
	右指针来存放单链表指针。
	分析：
		我们要将叶节点连起来，那么我们首先要按从左至右的顺序找出叶节点，要满足这样的出场顺序，可以采用先序，中序，后序，
		这里我们采用中序遍历。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
struct Stack {
	biTree *arr;
	int len;
	int top;
};
#include 
#include 
struct biTree *h = (struct biTree *)malloc(sizeof(struct biTree));//创建一个头结点
struct biTree *pre = h;
biTree *leafLink(biTree *b) {//将二叉树b中的所有叶子结点连起来
	if (b) {
		leafLink(b->lchild);//中序遍历左子树
		if (!b->lchild && !b->rchild) {//叶节点
				pre->rchild = b;
				pre = b;
			
		}
		leafLink(b->rchild);//中序遍历右子树
		pre->rchild = NULL;//设置链表尾
	}
	return h;
}
int main() {
	struct biTree *b = (struct biTree *)malloc(sizeof(struct biTree ));
	biTree *create(biTree *);
	b = create(b);//创建一颗二叉树
	leafLink(b);
	while (h->rchild) {
		printf("%c ", h->rchild->data);
		h = h->rchild;
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

判断两颗二叉树是否相似

/*
	试设计判断两课二叉树是否相似的算法。所谓二叉树T1和T2相似，指的是T1和T2都是空的二叉树或只有一个根节点；或二者左子树相似
	且左子树相似
	分析：
		典型的要采取递归来处理
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
};
#include 
#include 
bool isSimilar(biTree *T1, biTree *T2) {
	if (!T1 && !T2) {//T1,T2都是空的二叉树
		return true;
	}
	else if (!T1 || !T2) {//T1,T2只有一个为空，则不相似
		return false;
	}
	else {
		if (isSimilar(T1->lchild, T2->lchild) && isSimilar(T1->rchild, T2->rchild))//左右子树均相似，才相似
			return true;
		else
			return false;
	}

}
int main() {
	struct biTree *T1 = (struct biTree *)malloc(sizeof(struct biTree));
	struct biTree *T2 = (struct biTree *)malloc(sizeof(struct biTree));

	biTree *create(biTree *);
	printf("第一棵树数据：\n");

	T1 = create(T1);
	printf("\n");
	printf("第二棵树数据：\n");
	T2 = create(T2);

	isSimilar(T1, T2) ? printf("相似") : printf("不相似");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

中序线索二叉树中寻找某个节点的后序前驱

/*
	写出在中序线索二叉树里查找指定节点在后序的前驱结点的算法
	分析：
		在后序序列中，若节点p有右子女，则右子女是其前驱，若无右子女而有左子女，则左子女是其前驱。若节点p左右子女均无，
		设其中序左线索指向某祖先节点f(p是f右子树中按中序遍历的第一个节点)，若f有左子女，则其左子女是节点p在后序中的前驱；
		若f无左子女，则顺其前驱找双亲的双亲，一直找到双亲有左子女（此时左子女是p的前驱）。还有一种情况，若p是中序遍历的第
		一个节点，则节点p在中序和后序下均没有前驱。
*/
struct biTree {
	char data;
	struct biTree *lchild;
	struct biTree *rchild;
	int ltag, rtag;
};
#include 
#include 
biTree *findPre(biTree *T,biTree *p) {//返回前驱结点
	struct biTree *f;
	if (p->rchild&&p->rtag==0) {//若该节点有右孩子，那么右子女是其前驱
		return p->rchild;
	}
	else if(p->ltag==0&&p->lchild) {//若该节点只有左子女则左子女是其前驱
		return p->lchild;
	}
	else {
		f = p->lchild;//此时左线索指向某祖先节点
		while (f&&f->ltag) {//如果该祖先节点没有左子女，继续找前驱
			f = f->lchild;
		}
		if (f) {
			return f->lchild;
		}
		else {
			return NULL;
		}
	}
}
int main() {
	struct biTree *T = (struct biTree *)malloc(sizeof(struct biTree));
	biTree *create(biTree *);
	T = create(T);
	void inThread(biTree *,biTree *);
	inThread(T,NULL);//中序遍历建立线索

	struct biTree *p = T->rchild->lchild,*pre=NULL;//手动指定一个节点
	pre=findPre(T,p);
	if (pre) {
		printf("节点p%c的前驱结点值为：%c",p->data,pre->data);
	}
	else {
		printf("节点p没有前驱结点");
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

求叶节点带权路径长度-2014

/*
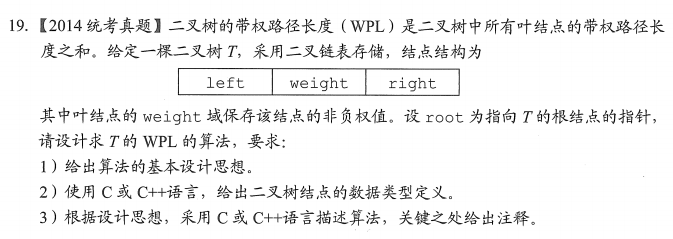
	二叉树的带权路径长度（WPL）是二叉树中所有叶节点的带权路径长度之和。给定一颗二叉树T,采用二叉链表存储，节点结构为
	left weight right
	试设计求T的WPL的算法
	分析：
		我们求带权路径长度，既需要知道叶节点的权值，也需要知道其经过的路径，我们可以设置一个变量depth代表深度，也就是
		路径长度，设置一个静态变量weight累加带权路径，会使用到递归。
*/
struct tree {
	int weight;
	struct tree *left, *right;
};
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
tree *create(tree *T) {//建立一颗二叉树
	int weight;
	printf("请输入当前节点权值：weight=");
	scanf("%d", &weight);
	getchar();
	if (weight != -1) {
		T = (tree *)malloc(sizeof(tree));
		T->weight = weight;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
int countWPL(tree *T, int depth) {
	static int totalWeight = 0;//设置静态变量
	if (T) {
		if (!T->left && !T->right) {//已经是叶节点
			totalWeight += T->weight*depth;//计算带权路径
		}
		else {
			countWPL(T->left, depth + 1);//左子树
			countWPL(T->right, depth + 1);//右子树
		}
	}
	return totalWeight;
}
int main() {
	struct tree *T = (struct tree *)malloc(sizeof(struct tree));
	T = create(T);
	int depth = 0;
	int totalW;
	totalW = countWPL(T, depth);
	printf("该二叉树的带权路径长度为：%d", totalW);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

中序输出表达式-2017

/*
	请设计一个算法，将给定的表达式树，转换成等价的中缀表达式并输出。
	分析：
		题目已然说明我们要采取中序遍历，进而输出该表达式，那么需要注意的点便是我们的括号在哪里加，其中根节点处和叶子结点
		处不需要添加括号，其余情况在访问左子树前加左括号，访问右子树后添加右括号
*/
struct BTree {
	char data;
	struct BTree *left, *right;
};
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

BTree *create(BTree *T) {//先序建立二叉树
	char data;
	printf("请输入当前节点值：data=");
	scanf("%c", &data);
	getchar();
	if (data != '#') {
		T = (BTree *)malloc(sizeof(BTree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
void putInExp(BTree *T,int deep) {
	if (T==NULL) {
		return;
	}
	if (!T->left&&!T->right) {//若为叶节点，直接输出操作数
		printf("%c",T->data);
	}
	else {
		if (deep > 1) printf("(");//非根节点，添加左括号
		putInExp(T->left,deep+1);
		printf("%c",T->data);
		putInExp(T->right, deep + 1);
		if (deep > 1) printf(")");

	}
}
int main() {
	struct BTree *T = (BTree *)malloc(sizeof(BTree));
	T = create(T);
	printf("中缀表达式为：");
	putInExp(T,1);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

孩子兄弟表示法的森林叶节点个数

/*
	编程求以孩子兄弟表示法存储的森林的叶子结点数
	分析：
			我们可以试想一个节点它如果有左孩子，那么根据孩子兄弟表示法的规则，那它一定不是叶节点，相反如果没有左孩子，那么
			它一定是叶子结点，其右孩子即它的兄弟，同样应该这样去判断。
*/
typedef struct node {
	char data;
	node *fch, *nsib;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

Tree *create(Tree *T) {//先序创建一颗二叉树
	char data;
	printf("请输入当前节点值：data=");
	scanf("%c", &data);
	getchar();
	if (data != '#') {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->fch = NULL;
		T->nsib = NULL;
		T->fch = create(T->fch);
		T->nsib = create(T->nsib);
	}
	return T;
}
int frostLeaf(Tree *T) {
	if (!T) {//空则返回0，也是递归的出口
		return 0;
	}
	else {
		if (!T->fch) {//没有左孩子，该节点为叶子结点
			return 1 + frostLeaf(T->nsib);
		}
		else {//有左孩子，该节点不是叶子结点
			return frostLeaf(T->fch) + frostLeaf(T->nsib);
		}
	}
}
int main() {
	Tree *T = (Tree *)malloc(sizeof(Tree *));
	T = create(T);
	printf("该森林的叶子结点个数为：%d", frostLeaf(T));
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

孩子兄弟链表法存储的树求高度

/*
	以孩子兄弟链表为存储结构，请设计递归算法求树的高度
	分析：
		如果只有根节点，那么高度为1，如果有左孩子，那么高度由左孩子的左子树和右子树决定，取其大者。
*/
typedef struct node {
	char data;
	node *fch, *nsib;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

Tree *create(Tree *T) {//先序创建一颗二叉树
	char data;
	printf("请输入当前节点值：data=");
	scanf("%c", &data);
	getchar();
	if (data != '#') {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->fch = NULL;
		T->nsib = NULL;
		T->fch = create(T->fch);
		T->nsib = create(T->nsib);
	}
	return T;
}
int getHigh(Tree *T) {
	int lhigh, rhigh;
	if (!T) {//空返回当前高度，这是递归的出口
		return 0;
	}
	else {
		lhigh = getHigh(T->fch);//记录左子树高度
		rhigh = getHigh(T->nsib);//记录右兄弟的高度，注意这里high不能再加一，因为他们是兄弟，平级
		if (lhigh + 1 > rhigh) {
			return lhigh + 1;
		}
		else {
			return rhigh;
		}
	}
}
int main() {
	Tree *T = (Tree *)malloc(sizeof(Tree *));
	T = create(T);
	int high = 0;
	high = getHigh(T);
	printf("树的高度为：%d", high);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

已知树的层次序列及各节点的度，构造孩子兄弟链表

/*
	从所给的树的层次遍历及其节点度数，构造孩子兄弟链表
	分析：
		这里设计到层次遍历，还有孩子-兄弟链表，较为复杂。我们可以设立一个类型为树节点的数组，
		将层次序列里面的所有值放到该数组中，将其所有节点的fch和sub值为空
		然后一次去遍历节点，取出度数d，若d>0,说明该节点有孩子，将第一个孩子放到左指针fch，其他孩子
		一次放到sub中，注意这里会有变化，代码里再详说
*/
typedef struct node {
	char data;
	node *fch, *nsib;
}Tree;
#include
#include 
void createCSTree_degree(char *level, int *degree, node **pointer, int n) {
	int k = 0;//判断到了哪个节点
	for (int i = 0; i < n; i++) {//初始化pointer
		pointer[i]->data = level[i];
		pointer[i]->fch = NULL;
		pointer[i]->nsib = NULL;
	}
	for (int i = 0; i < n; i++) {
		int d = degree[i];
		if (d) {
			k++;//k为子女节点序号
			pointer[i]->fch = pointer[k];
			for (int j = 0; j < d - 1; j++) {
				k++;
				pointer[k - 1]->nsib = pointer[k];
			}
		}
	}

}
void inOrder(node *T) {
	if (T) {
		inOrder(T->fch);
		printf("%c ", T->data);
		inOrder(T->nsib);
	}
};
int main() {
	char level[6] = { 'A','B','E','G','D','F' };//层次遍历，用数组存储
	int degree[] = { 3,2,0,0,0,0 };
	node* *pointer = (node* *)malloc(sizeof(node*) * 6);
	for (int i = 0; i < 6; i++) {
		pointer[i] = (node*)malloc(sizeof(node*));
	}
	createCSTree_degree(level, degree, pointer, 6);
	inOrder(pointer[0]);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

判断是否是一颗二叉排序树

/*
	编写一个算法判断给定的二叉树是否是二叉排序树
	分析：
		二叉排序树的中序序列是升序序列，我们可以根据这一特性来进行判定
*/
typedef struct node {
	int data;
	node *left, *right;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
Tree *create(Tree *T) {//先序创建一颗二叉树
	int data;
	printf("请输入当前节点值：data=");
	scanf("%d", &data);
	getchar();
	if (data != -1) {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
bool isSortTree(Tree *T) {
	static int min = -32768;//最开始设定min为最小值，确保第一个节点能够进行下去
	static bool flag = true;//作为是否是升序的标记，采用静态变量，不然每次都会初始化
	if (T) {
		isSortTree(T->left);
		if (T->data < min)
			flag = false;
		else
			min = T->data;//min 1
		isSortTree(T->right);
	}
	return flag;
}
int main() {
	//先创建一颗二叉树
	Tree *T = (Tree *)malloc(sizeof(Tree *));
	T = create(T);
	isSortTree(T) ? printf("是二叉排序树") : printf("不是二叉排序树");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

求指定节点在二叉排序树中的层次

/*
	设计一个算法，求出指定节点在给定二叉排序树中的层次
	分析：
		我们可以根据二叉排序树的性质，从根节点一直向下查找，每查找一次，层次便加一
*/
typedef struct node {
	int data;
	node *left, *right;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

Tree *create(Tree *T) {//先序创建一颗二叉树
	int data;
	printf("请输入当前节点值：data=");
	scanf("%d", &data);
	getchar();
	if (data != -1) {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
void findLevel(Tree *T, int p,int &depth) {
	if (T) {
		if (T->data < p) {
			depth++;
			findLevel(T->right, p,depth);
		}
		else if(T->data > p){
			depth++;
			findLevel(T->left, p,depth);
		}
	}
}
int main() {
	//创建一颗二叉排序树
	Tree *T = (Tree *)malloc(sizeof(Tree *));
	T = create(T);
	int p = 7,depth=1;//手动指定节点值
	findLevel(T,p,depth);
	printf("该节点所在的层次为第%d层",depth);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

判断一颗二叉树是否是平衡二叉树

/*
	利用二叉树遍历的思想编写一个判断二叉树是否是二叉平衡树的算法
	分析：
		我们可以采取后序遍历来完成该算法，因为后序遍历不会含有重复计算。
		我们对每一个节点进行判断，如果左右子树均平衡且左右子树高度差小于等于1，则该节点平衡

*/
struct Tree {
	int data;
	Tree *left, *right;
};
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
Tree *create(Tree *T) {//先序创建一颗二叉树
	int data;
	printf("请输入当前节点值：data=");
	scanf("%d", &data);
	getchar();
	if (data != -1) {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
bool isAVL(Tree *T, int *depth) {
	if (!T) {//空节点，为平衡二叉树
		*depth = 0;
		return true;
	}
	int left = 0, right = 0;
	if (isAVL(T->left, &left) && isAVL(T->right, &right)) {//判断左右子树是否为平衡二叉树
		int diff = left - right;//左右子树的高度差
		if (abs(diff) <= 1) {//满足小于等于1,那就是平衡二叉树
			*depth	= (1 + (left > right ? left : right));
			return true;
		}
	}
	return false;//前面一直未返回true，那就不是平衡二叉树
}
int main() {
	Tree *T = (Tree *)malloc(sizeof(Tree *));
	T = create(T);//创建一颗二叉树
	int depth = 0;
	isAVL(T, &depth) ? printf("是二叉平衡树"):printf("不是二叉平衡树");
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

查找二叉平衡树中第k小的元素

/*
	编写一个递归算法，在一棵有n个节点的、随机建立起来的二叉排序树上查找第k小的元素，并返回指向该节点的指针，要求算法的平均
	时间复杂度为O(logn)。二叉排序树的每个节点中除了data、lchild、rchild等数据成员外，增加一个count成员，保存以该节点为根的
	子树的节点个数
	分析：
		这里要求时间复杂度为O(ln)，我们就不能采用常规的方法了，这里我们需要利用递归的思想，将各种情况罗列清楚
		一、t->lchild 为空
		①如果t->rchild 非空 且 k=1，那么根据二叉排序树的特性 t即为第k小
		②如果t->rchild 非空 且 k!=1，那么第k小的数肯定在右子树中
		二、如果t->lchild 非空
		①如果t->lchild->count ==k-1,那么t即为第k小
		②如果t->lchild->count > k-1,那么第k小在左子树
		③如果t->lchild->count < k-1,那么第k小在右子树，寻找第k-(t->lchild->count +1)小的元素

		这道题的那点就在于对问题的分析，我们很容易就遗漏某些情况，导致代码逻辑有问题，需要注意


*/

typedef struct node {
	int data;
	int count;//子树节点个数
	struct node *left, *right;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

Tree *create(Tree *T) {//先序创建一颗排序二叉树
	int data;
	printf("请输入当前节点值：data=");
	scanf("%d", &data);
	getchar();
	if (data != -1) {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
int getCount(Tree *T) {//统计每个节点的以它为根的子树上的节点个数
	if (!T)return 0;
	int lcount, rcount;
	lcount = getCount(T->left);
	rcount = getCount(T->right);
	T->count = lcount + rcount + 1;
	return lcount + rcount + 1;
}
Tree *findKth(Tree *T, int k) {
	if (k<1 || k>T->count)return NULL;
	if (!T->left) {
		if (k == 1) return T;
		else return findKth(T->right, k - 1);

	}
	else {
		if (T->left->count == k - 1) return T;
		if (T->left->count > k - 1) return findKth(T->left, k);

		if (T->left->count < k - 1) return findKth(T->right, k - (T->left->count + 1));
	}
}
int main() {
	Tree *T = (Tree *)malloc(sizeof(Tree));
	Tree *p;
	int k = 5;
	T = create(T);
	getCount(T);
	p = findKth(T, k);
	if (p) {
		printf("第 %d 小的节点值为 %d",k,p->data);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

0G6uyVf-1658998825489)]

/*
	编写一个递归算法，在一棵有n个节点的、随机建立起来的二叉排序树上查找第k小的元素，并返回指向该节点的指针，要求算法的平均
	时间复杂度为O(logn)。二叉排序树的每个节点中除了data、lchild、rchild等数据成员外，增加一个count成员，保存以该节点为根的
	子树的节点个数
	分析：
		这里要求时间复杂度为O(ln)，我们就不能采用常规的方法了，这里我们需要利用递归的思想，将各种情况罗列清楚
		一、t->lchild 为空
		①如果t->rchild 非空 且 k=1，那么根据二叉排序树的特性 t即为第k小
		②如果t->rchild 非空 且 k!=1，那么第k小的数肯定在右子树中
		二、如果t->lchild 非空
		①如果t->lchild->count ==k-1,那么t即为第k小
		②如果t->lchild->count > k-1,那么第k小在左子树
		③如果t->lchild->count < k-1,那么第k小在右子树，寻找第k-(t->lchild->count +1)小的元素

		这道题的那点就在于对问题的分析，我们很容易就遗漏某些情况，导致代码逻辑有问题，需要注意


*/

typedef struct node {
	int data;
	int count;//子树节点个数
	struct node *left, *right;
}Tree;
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

Tree *create(Tree *T) {//先序创建一颗排序二叉树
	int data;
	printf("请输入当前节点值：data=");
	scanf("%d", &data);
	getchar();
	if (data != -1) {
		T = (Tree *)malloc(sizeof(Tree));
		T->data = data;
		T->left = NULL;
		T->right = NULL;
		T->left = create(T->left);
		T->right = create(T->right);
	}
	return T;
}
int getCount(Tree *T) {//统计每个节点的以它为根的子树上的节点个数
	if (!T)return 0;
	int lcount, rcount;
	lcount = getCount(T->left);
	rcount = getCount(T->right);
	T->count = lcount + rcount + 1;
	return lcount + rcount + 1;
}
Tree *findKth(Tree *T, int k) {
	if (k<1 || k>T->count)return NULL;
	if (!T->left) {
		if (k == 1) return T;
		else return findKth(T->right, k - 1);

	}
	else {
		if (T->left->count == k - 1) return T;
		if (T->left->count > k - 1) return findKth(T->left, k);

		if (T->left->count < k - 1) return findKth(T->right, k - (T->left->count + 1));
	}
}
int main() {
	Tree *T = (Tree *)malloc(sizeof(Tree));
	Tree *p;
	int k = 5;
	T = create(T);
	getCount(T);
	p = findKth(T, k);
	if (p) {
		printf("第 %d 小的节点值为 %d",k,p->data);
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77