-
Python数据分析与机器学习33-K-Means实例
一. 数据源介绍
数据源:
一个啤酒的数据源，为了方便演示，数据只有20行。
- name 啤酒的名称
- calories 啤酒的卡路里
- sodium 纳元素含量
- alcohol 酒精含量
- cost 价格
二. 使用K-means进行聚类
代码:
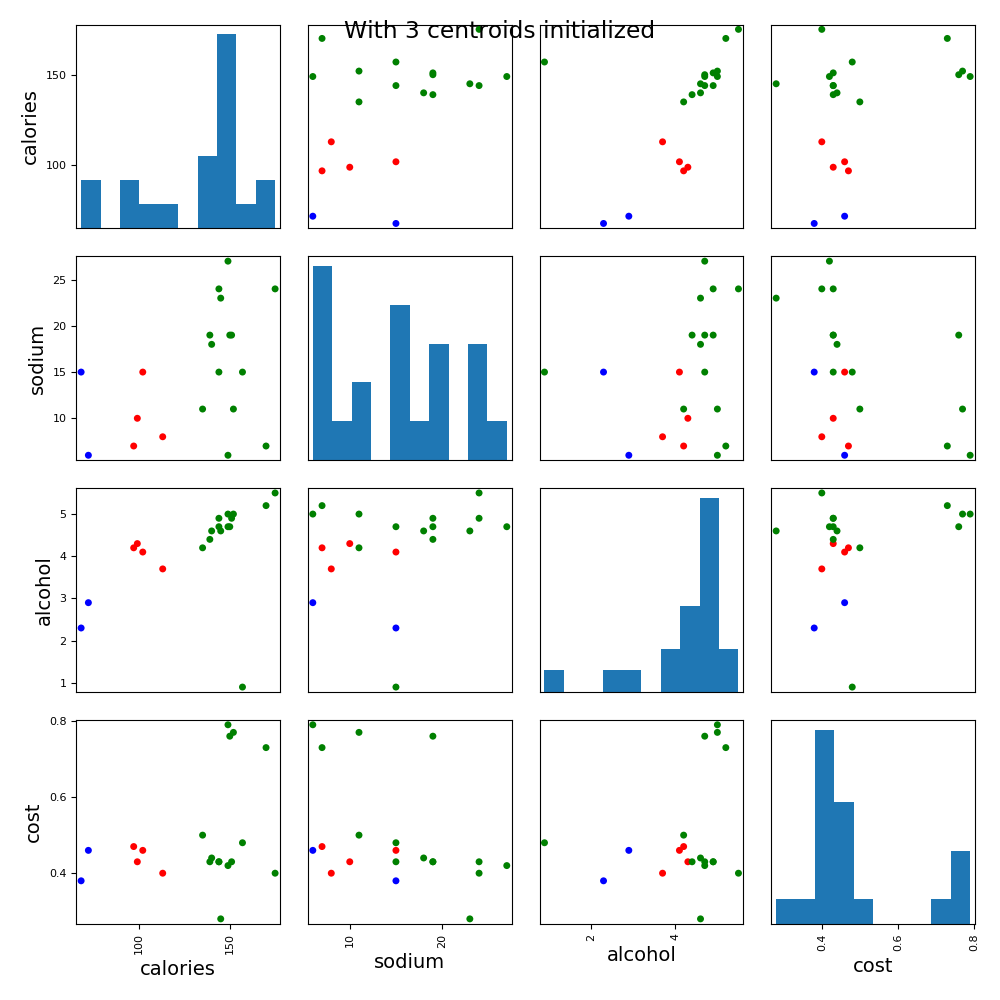
import pandas as pd from sklearn.cluster import KMeans from pandas.plotting import scatter_matrix import matplotlib.pyplot as plt import numpy as np # 读取数据源 beer = pd.read_csv('E:/file/data.txt', sep=' ') X = beer[["calories","sodium","alcohol","cost"]] # 训练两个模型，一个2个簇，一个3个簇 km = KMeans(n_clusters=3).fit(X) km2 = KMeans(n_clusters=2).fit(X) # 输出模型的label print ("模型的label:" , km.labels_) # 将标签新增到数据源上 beer['cluster'] = km.labels_ beer['cluster2'] = km2.labels_ print ("增加聚类标签后的数据:") print(beer.sort_values('cluster')) print ("输出聚类2各个特征值的均值:") print(beer.groupby("cluster2").mean()) # pandas 绘制散点图 cluster_centers = km.cluster_centers_ cluster_centers_2 = km2.cluster_centers_ centers = beer.groupby("cluster").mean().reset_index() plt.rcParams['font.size'] = 14 colors = np.array(['red', 'green', 'blue', 'yellow']) scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster"]], figsize=(10,10)) plt.suptitle("With 3 centroids initialized") plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
测试记录:
模型的label: [1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 2 1 1 2 0] 增加聚类标签后的数据: name calories sodium ... cost cluster cluster2 9 Budweiser_Light 113 8 ... 0.40 0 1 11 Coors_Light 102 15 ... 0.46 0 1 8 Miller_Lite 99 10 ... 0.43 0 1 19 Schlitz_Light 97 7 ... 0.47 0 1 4 Heineken 152 11 ... 0.77 1 0 5 Old_Milwaukee 145 23 ... 0.28 1 0 6 Augsberger 175 24 ... 0.40 1 0 7 Srohs_Bohemian_Style 149 27 ... 0.42 1 0 2 Lowenbrau 157 15 ... 0.48 1 0 10 Coors 140 18 ... 0.44 1 0 1 Schlitz 151 19 ... 0.43 1 0 12 Michelob_Light 135 11 ... 0.50 1 0 13 Becks 150 19 ... 0.76 1 0 14 Kirin 149 6 ... 0.79 1 0 16 Hamms 139 19 ... 0.43 1 0 17 Heilemans_Old_Style 144 24 ... 0.43 1 0 3 Kronenbourg 170 7 ... 0.73 1 0 0 Budweiser 144 15 ... 0.43 1 0 18 Olympia_Goled_Light 72 6 ... 0.46 2 1 15 Pabst_Extra_Light 68 15 ... 0.38 2 1 [20 rows x 7 columns] 输出聚类2各个特征值的均值: calories sodium alcohol cost cluster cluster2 0 150.000000 17.000000 4.521429 0.520714 1.000000 1 91.833333 10.166667 3.583333 0.433333 0.666667- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
三. 数据归一化
代码:
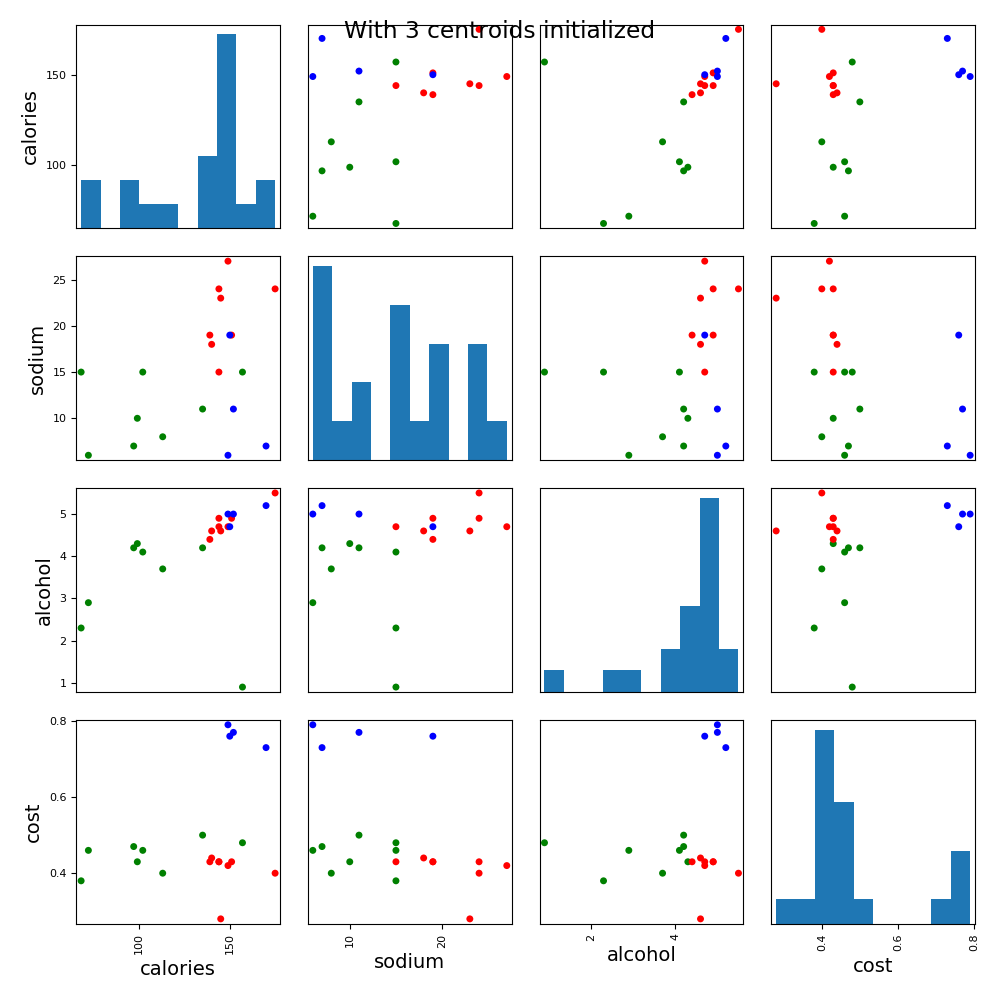
import pandas as pd from sklearn.cluster import KMeans from pandas.plotting import scatter_matrix import matplotlib.pyplot as plt import numpy as np from sklearn.preprocessing import StandardScaler # 读取数据源 beer = pd.read_csv('E:/file/data.txt', sep=' ') X = beer[["calories","sodium","alcohol","cost"]] # 对数据进行与处理 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) print ("归一化后的数据集:" ) print(X_scaled) # 训练两个模型，一个2个簇，一个3个簇 km = KMeans(n_clusters=3).fit(X_scaled) km2 = KMeans(n_clusters=2).fit(X_scaled) # 输出模型的label print ("模型的label:" , km.labels_) # 将标签新增到数据源上 beer['cluster'] = km.labels_ beer['cluster2'] = km2.labels_ print ("增加聚类标签后的数据:") print(beer.sort_values('cluster')) print ("输出聚类2各个特征值的均值:") print(beer.groupby("cluster2").mean()) # pandas 绘制散点图 cluster_centers = km.cluster_centers_ cluster_centers_2 = km2.cluster_centers_ centers = beer.groupby("cluster").mean().reset_index() plt.rcParams['font.size'] = 14 colors = np.array(['red', 'green', 'blue', 'yellow']) scatter_matrix(beer[["calories","sodium","alcohol","cost"]],s=100, alpha=1, c=colors[beer["cluster"]], figsize=(10,10)) plt.suptitle("With 3 centroids initialized") plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
测试记录:
归一化后的数据集: [[ 0.38791334 0.00779468 0.43380786 -0.45682969] [ 0.6250656 0.63136906 0.62241997 -0.45682969] [ 0.82833896 0.00779468 -3.14982226 -0.10269815] [ 1.26876459 -1.23935408 0.90533814 1.66795955] [ 0.65894449 -0.6157797 0.71672602 1.95126478] [ 0.42179223 1.25494344 0.3395018 -1.5192243 ] [ 1.43815906 1.41083704 1.1882563 -0.66930861] [ 0.55730781 1.87851782 0.43380786 -0.52765599] [-1.1366369 -0.7716733 0.05658363 -0.45682969] [-0.66233238 -1.08346049 -0.5092527 -0.66930861] [ 0.25239776 0.47547547 0.3395018 -0.38600338] [-1.03500022 0.00779468 -0.13202848 -0.24435076] [ 0.08300329 -0.6157797 -0.03772242 0.03895447] [ 0.59118671 0.63136906 0.43380786 1.88043848] [ 0.55730781 -1.39524768 0.71672602 2.0929174 ] [-2.18688263 0.00779468 -1.82953748 -0.81096123] [ 0.21851887 0.63136906 0.15088969 -0.45682969] [ 0.38791334 1.41083704 0.62241997 -0.45682969] [-2.05136705 -1.39524768 -1.26370115 -0.24435076] [-1.20439469 -1.23935408 -0.03772242 -0.17352445]] 模型的label: [0 0 1 2 2 0 0 0 1 1 0 1 1 2 2 1 0 0 1 1] 增加聚类标签后的数据: name calories sodium ... cost cluster cluster2 0 Budweiser 144 15 ... 0.43 0 1 1 Schlitz 151 19 ... 0.43 0 1 17 Heilemans_Old_Style 144 24 ... 0.43 0 1 16 Hamms 139 19 ... 0.43 0 1 5 Old_Milwaukee 145 23 ... 0.28 0 1 6 Augsberger 175 24 ... 0.40 0 1 7 Srohs_Bohemian_Style 149 27 ... 0.42 0 1 10 Coors 140 18 ... 0.44 0 1 15 Pabst_Extra_Light 68 15 ... 0.38 1 0 12 Michelob_Light 135 11 ... 0.50 1 1 11 Coors_Light 102 15 ... 0.46 1 0 9 Budweiser_Light 113 8 ... 0.40 1 0 8 Miller_Lite 99 10 ... 0.43 1 0 2 Lowenbrau 157 15 ... 0.48 1 0 18 Olympia_Goled_Light 72 6 ... 0.46 1 0 19 Schlitz_Light 97 7 ... 0.47 1 0 13 Becks 150 19 ... 0.76 2 1 14 Kirin 149 6 ... 0.79 2 1 4 Heineken 152 11 ... 0.77 2 1 3 Kronenbourg 170 7 ... 0.73 2 1 [20 rows x 7 columns] 输出聚类2各个特征值的均值: calories sodium alcohol cost cluster cluster2 0 101.142857 10.857143 3.2 0.440000 1.000000 1 149.461538 17.153846 4.8 0.523846 0.692308- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
四. 聚类评估：轮廓系数（Silhouette Coefficient ）
-
计算样本i到同簇其他样本的平均距离ai。ai 越小，说明样本i越应该被聚类到该簇。将ai 称为样本i的簇内不相似度。
-
计算样本i到其他某簇Cj 的所有样本的平均距离bij，称为样本i与簇Cj 的不相似度。定义为样本i的簇间不相似度：bi =min{bi1, bi2, …, bik}
-
si接近1，则说明样本i聚类合理
-
si接近-1，则说明样本i更应该分类到另外的簇
-
若si 近似为0，则说明样本i在两个簇的边界上。
代码:
import pandas as pd from sklearn.cluster import KMeans from pandas.plotting import scatter_matrix import matplotlib.pyplot as plt import numpy as np from sklearn.preprocessing import StandardScaler from sklearn import metrics # 读取数据源 beer = pd.read_csv('E:/file/data.txt', sep=' ') X = beer[["calories","sodium","alcohol","cost"]] # 对数据进行与处理 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 训练两个模型，一个是原始数据，一个是归一化后的数据 km = KMeans(n_clusters=3).fit(X) km2 = KMeans(n_clusters=2).fit(X_scaled) # 将标签新增到数据源上 beer['cluster'] = km.labels_ beer['scaled_cluster'] = km2.labels_ score_scaled = metrics.silhouette_score(X,beer.scaled_cluster) score = metrics.silhouette_score(X,beer.cluster) print("输出归一化评分及原始数据样本评分:") print(score_scaled, score) # 查看不同K值下的评分 scores = [] for k in range(2,20): labels = KMeans(n_clusters=k).fit(X).labels_ score = metrics.silhouette_score(X, labels) scores.append(score) print("查看不同K值评分:") print(scores) plt.plot(list(range(2,20)), scores) plt.xlabel("Number of Clusters Initialized") plt.ylabel("Sihouette Score") plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
测试记录:
输出归一化评分及原始数据样本评分: 0.5562170983766765 0.6731775046455796 查看不同K值评分: [0.6917656034079486, 0.6731775046455796, 0.5857040721127795, 0.422548733517202, 0.4559182167013377, 0.43776116697963124, 0.38946337473125997, 0.39746405172426014, 0.3915697409245163, 0.41282646329875183, 0.3459775237127248, 0.31221439248428434, 0.30707782144770296, 0.31834561839139497, 0.2849514001174898, 0.23498077333071996, 0.1588091017496281, 0.08423051380151177]- 1
- 2
- 3
- 4
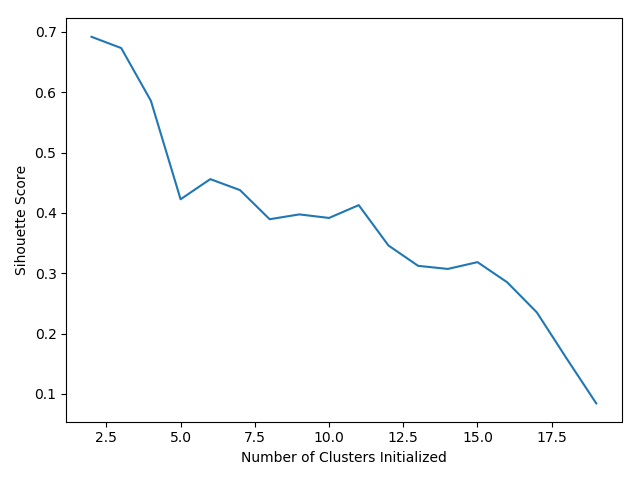
分析:
归一化之后，居然效果没有原始数据集好，估计是样本太简单了吧，多数情况下作了归一化之后，效果会有一定程度的提升。参考：
- https://study.163.com/course/introduction.htm?courseId=1003590004#/courseDetail?tab=1
-
相关阅读:
【数据可视化】动态条形图Python代码实现
秦简总经理王建忠：论都江堰泛计算操作系统的商业价值
Leecode 周赛318场
OSI七层参考模型和TCP/IP四层(五层)参考模型
SLAM从入门到精通（被忽视的基础图像处理）
PASS计算样本量（1）---完全随机设计时两样本率比较
基于Java的药品管理系统设计与实现(源码+lw+部署文档+讲解等)
HCIA-HarmonyOS设备开发V2.0证书
JAVA微服务知识概述
站点到站点的流量监控
- 原文地址：https://blog.csdn.net/u010520724/article/details/126029833