斐波那契数列的递归优化《备忘录递归》

暴力递归

斐波那契数列的数学形式就是递归，直接上代码：

public static int fibonacci(int n) {
        if (n <= 2) {
            return 1;
        }
        return fibonacci(n - 1) + fibonacci(n - 2);
    }
1
2
3
4
5
6

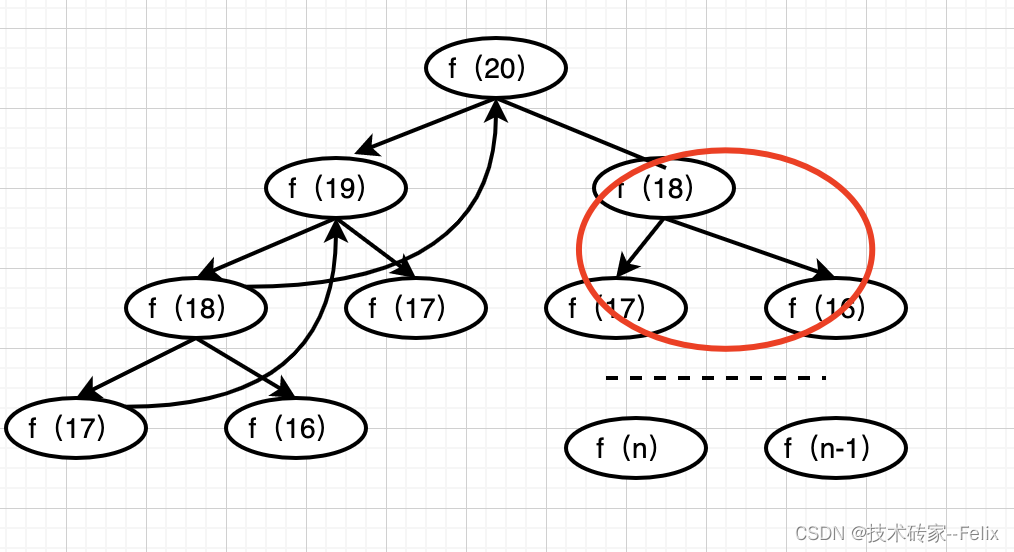
根据斐波那契数列的特性，我们画出他的递归树：

根据递归树，可以看出，要计算f（20）就得计算出f（19）+f（18），以此类推。遇到f(1),f(2)结果已知，这样递归树不再增长，可以直接返回结果。

递归的时间复杂度

时间复杂度=子问题的个数乘以解决一个子问题需要的时间。

递归树中节点的个数为 二叉树的节点，即2ⁿ⁺¹ 次方减1（n为树的高度），指数级别，所以求子问题的时间复杂度为O(2ⁿ).

在斐波那契的暴力递归中，解决子问题的时间没有循环，故时间复杂度为O(1).

最终得时间复杂度为出O(1)*O(2ⁿ)=O(2ⁿ)

但是根据递归树可以看出，f（18）被计算了两次，诸如此类，有很多大量的重复的计算，消耗时间，低效，就是动态规划的第一个性质重叠子问题。

带备忘录的递归算法

备忘录就是我们把重复的计算结果存储到备忘录里，遇到之后直接查出来，不再去计算（递归）一遍，一般可以用一个数组或者其他集合充当备忘录。

上代码：

    /**
     * 备忘录递归.
     *
     * @param memo 备忘录集合，每个元素被赋予0。
     * @param n 数列长度
     * @return 结果
     */
    public static int fibonacciMemo(List<Integer> memo, int n) {
        if (n <= 2) {
            return 1;
        }
        //直接返回备忘录里的值
        if (memo.get(n) != 0) {
            return memo.get(n);
        }
        //添加到备忘录
        memo.add(n, fibonacciMemo(memo, n - 1) + fibonacciMemo(memo, n - 2));
        return memo.get(n);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

加了备忘录的递归树：

带备忘录的递归算法就是把一颗巨大冗余的递归树通过剪裁，改造成了不冗余的递归图，减少子问题的解决

自顶向下

带备忘录的递归算法时间复杂度

根据时间复杂的公式：

子问题的求解时间复杂度等于 O(1)。

由于改造后不涉及冗余计算子问题的数量变成了线形的，为O(n).

最后的时间复杂度也为O(n).