在处理时序数据，已经有RNN循环神经网络和GRU神经网络两个比较经典的网络。当然还有一种LSTM神经网络，长短期记忆神经网络。
从发展历史来看，是现有LSTM再有GRU的，但是从复杂度来看，LSTM比GRU更加复杂。

先来回忆一下GRU，其有两个门（更新门和重置门），有一个记录历史信息的向量$H_t$。
而LSTM就更加复杂了，无论是在门的数量上还是记录历史信息的向量上。

LSTM神经网络

其一共有3个门，2个状态。

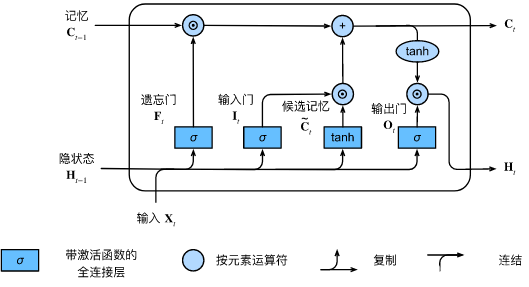
控制门

遗忘门

这个与GRU中的重置门非常类似，含义也是大致相同。
$$F_t=\Theta \left(X_t\cdot W_{xf}+H_{t-1}\cdot W_{hf}+b_f\right)$$
而后，$F_t$作用于记忆$C_{t-1}$，遗忘部分历史信息。

输入门

它与GRU中的更新门有点类似，但是却不完全一样。
因为LSTM有两个状态，它可以理解为$C_t$的更新门。
$$I_t=\Theta \left(X_t\cdot W_{xi}+H_{t-1}\cdot W_{hi}+b_i\right)$$
其后会作用于候选记忆$C_t^{\prime }$，更新得出新的$C_t$。

输出门

它与GRU中的更新门有点类似，但是却不完全一样。
因为LSTM有两个状态，它可以理解为$H_t$的更新门。
$$O_t=\Theta \left(X_t\cdot W_{xo}+H_{t-1}\cdot W_{ho}+b_o\right)$$
其后会作用于候选记忆$C_t$，更新得出新的$H_t$。

状态

记忆状态

从整个更新过程可以看到，$C_{t-1}$先遗忘部分信息，再与候选记忆（根据$X_t$）生成出的部分信息合并，得到$C_t$。
其的变化是较为缓慢的，也被成为长期记忆。

隐状态

$H_t$根据目前的输出（$X_t$与$H_{t-1}$的结果）与当前记忆$C_t$作用的结果。相比于$C_t$，$H_t$与$H_{t-1}$关系更弱，因此$H_t$变化更加的快。因此也被称为短期记忆。

结合上述两个状态：长期记忆与短期记忆，其就被称为长短期记忆神经网络。

代码实现

pytorch也提供了对于的LSTM层，可以十分方便的调用。
但是需要自己定义创始状态值（一个二元组）。

class LSMT_Net(nn.Module):
    def __init__(self, vocab_size, hidden_size, **kwargs):
        super(LSMT_Net, self).__init__(**kwargs)
        self.vocab_size = vocab_size
        self.hidden_size = hidden_size
        self.LSMTlayer = nn.LSTM(vocab_size , hidden_size, num_layers= 2)
        self.L1 = nn.Linear(hidden_size , vocab_size)
    def forward(self, inputs, state):
        X = F.one_hot(inputs.T.long(), self.vocab_size) # 转变成一个只有一个1，其余都是0的向量
        X = X.to(torch.float32)        
        Y , state = self.LSMTlayer(X , state)
        Y = Y.reshape((-1 , Y.shape[-1]))
        Y = self.L1(Y)
        return Y , state
    def begin_state(self , batch_size):
        return (torch.zeros(self.LSMTlayer.num_layers , batch_size , self.hidden_size),
               torch.zeros(self.LSMTlayer.num_layers , batch_size , self.hidden_size))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17