leetcode 剑指 Offer 63. 股票的最大利润

    因此，暴力法的时间复杂度为 O(n2) 。考虑使用动态规划降低时间复杂度，以下按照流程解题。

动态规划

    状态定义： 设动态规划列表 dp ，dp[i] 代表以 prices[i] 为结尾的子数组的最大利润（以下简称为 前 i日的最大利润 ）。
    转移方程： 由于题目限定 “买卖该股票一次” ，因此前 i 日最大利润 dp[i] 等于前 i−1 日最大利润 dp[i−1]和第 i 日卖出的最大利润中的最大值。

前i日最大利润=max⁡(前(i−1)日最大利润,第i日价格−前i日最低价格)

dp[i]=max⁡(dp[i−1],prices[i]−min⁡(prices[0:i]))

    初始状态： dp[0]=0dp[0] = 0dp[0]=0 ，即首日利润为 000 ；
    返回值： dp[n−1]dp[n - 1]dp[n−1] ，其中 nnn 为 dpdpdp 列表长度。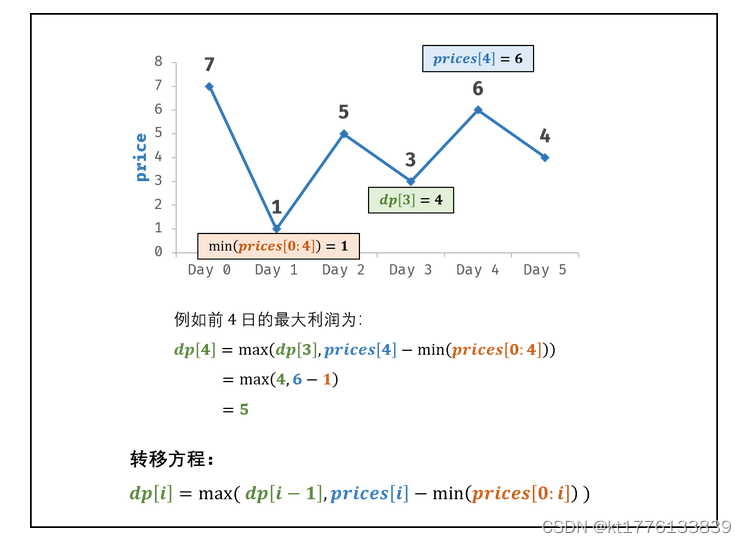

Java程序：

class Solution {
    public int maxProfit(int[] prices) {
        int cost = Integer.MAX_VALUE, profit = 0;
        for(int price : prices) {
            cost = Math.min(cost, price);
            profit = Math.max(profit, price - cost);
        }
        return profit;
    }
}