AVL树简介

AVL树是由GM Adelson - Velsky和EM Landis于1962年发明的。为了纪念其发明者，这树结构被命名为AVL。

AVL树可以定义为高度平衡二叉搜索树，其中每个节点与平衡因子相关联，该平衡因子通过从其左子树的子树中减去其右子树的高度来计算。

如果每个节点的平衡因子在-1到1之间，则称树是平衡的，否则，树将是不平衡的并且需要平衡。

平衡系数(k)=高度(左(k)) - 高度(右(k))

如果任何节点的平衡因子为1，则意味着左子树比右子树高一级。如果任何节点的平衡因子为0，则意味着左子树和右子树包含相等的高度。如果任何节点的平衡因子是-1，则意味着左子树比右子树低一级。

AVL树如下图所示。 可以看到，与每个节点相关的平衡因子介于-1和+1之间。 因此，它是AVL树的一个例子。

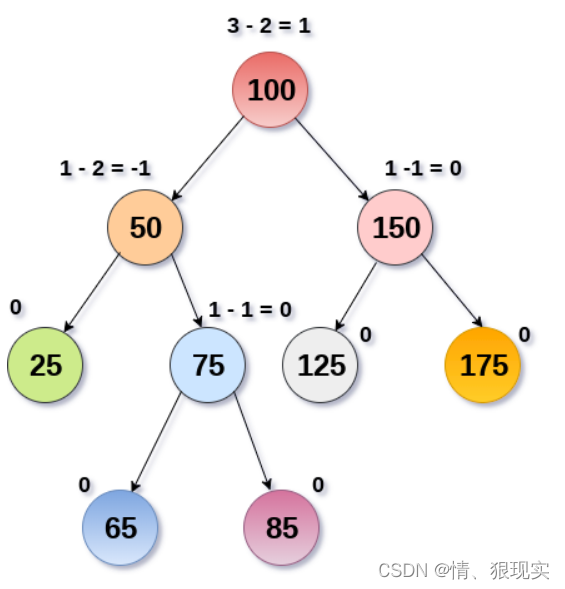
复杂性

AVL树插入元素

AVL树中的插入的执行方式与在二叉搜索树中执行的方式相同。 新节点作为叶节点添加到AVL树中。 但是，它可能会导致违反AVL树属性，因此树可能需要平衡。

可以通过应用旋转来平衡树。 仅当插入新节点时任何节点的平衡因子受到干扰时才需要旋转，否则不需要旋转。

根据插入的类型，旋转分为四类。

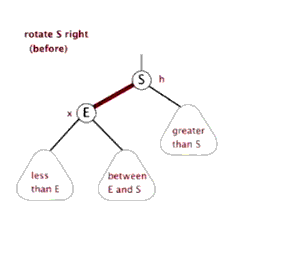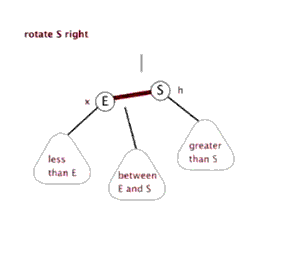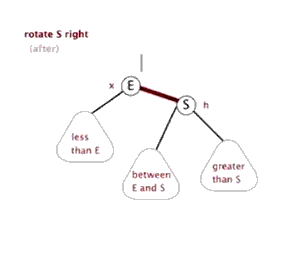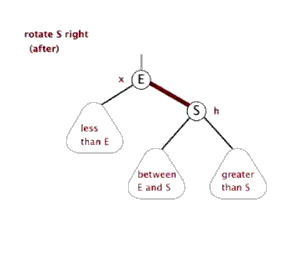
LL 右旋

新节点被插入到关键节点的左子树的左子树中

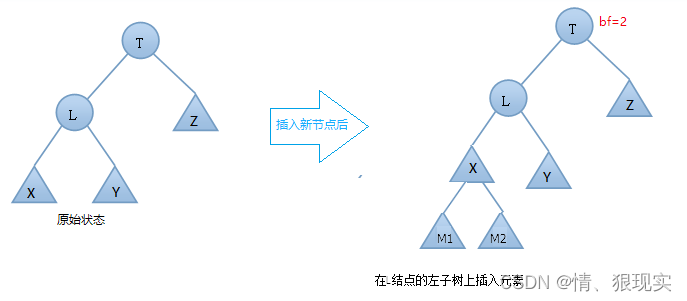
LL 右旋旋转步骤

• T向右旋转成为L的右节点
• L的右节点Y 移动到 T的左节点上

旋转中心是根节点T的左节点（L）

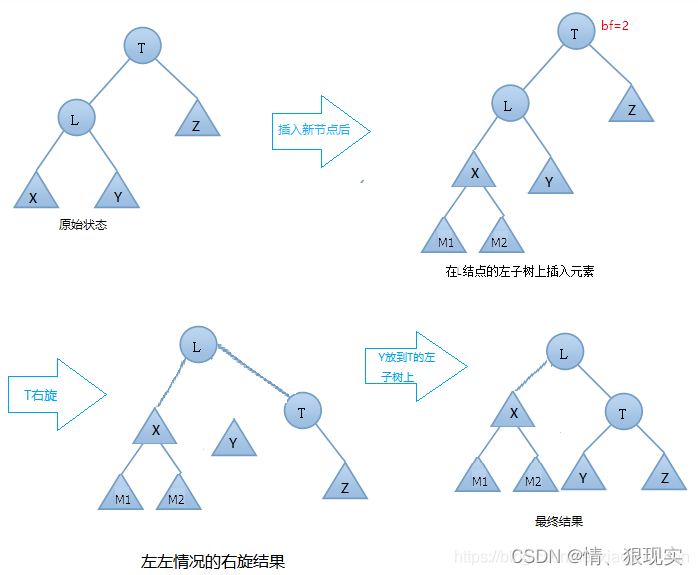
右旋动图

LR 左右旋

新节点被插入到关键节点的左子树的右子树中

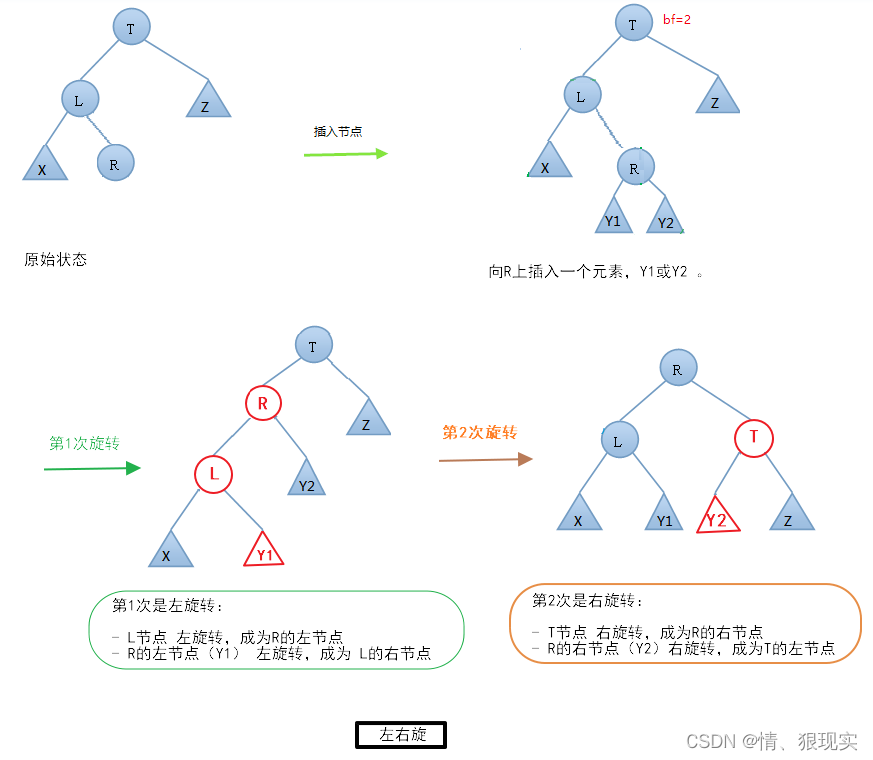
LR 左右旋 两次旋转步骤

1. 左旋转
   • L节点 左旋转，成为R的左节点
   • R的左节店(Y1)左旋转，成为L的右节点（左子节点左转）
2. 右旋转
   • T节点 右旋转，成为R的右节点
   • R的右节点(Y2)右旋转，成为T的左节点（右子节点右转）

旋转中心是根节点T的左节点（R）

RR 左旋

新节点被插入到关键节点的右子树的右子树中

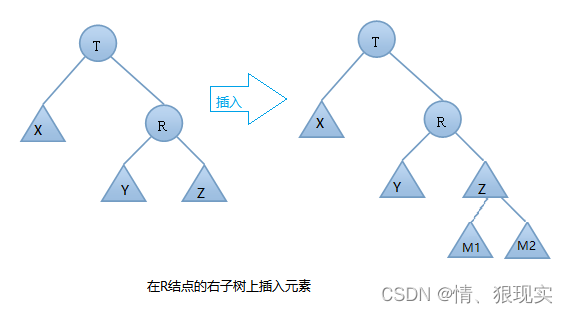
RR 左旋步骤

• T向左旋转成为R的左结点
• R的左节点Y放到T的右节点上

旋转中心是根节点T的右节点（R）。

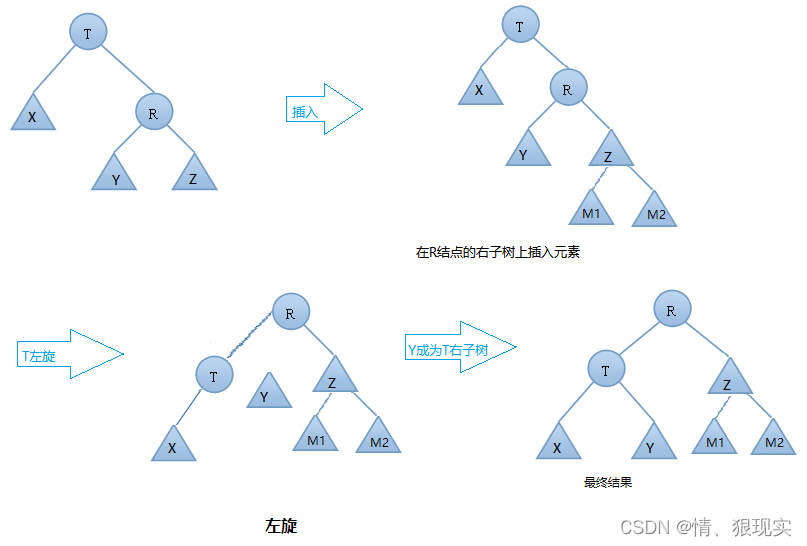
左旋动图

RL 右左旋

新节点被插入到关键节点的右子树的左子树中

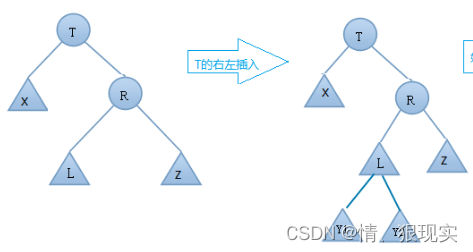
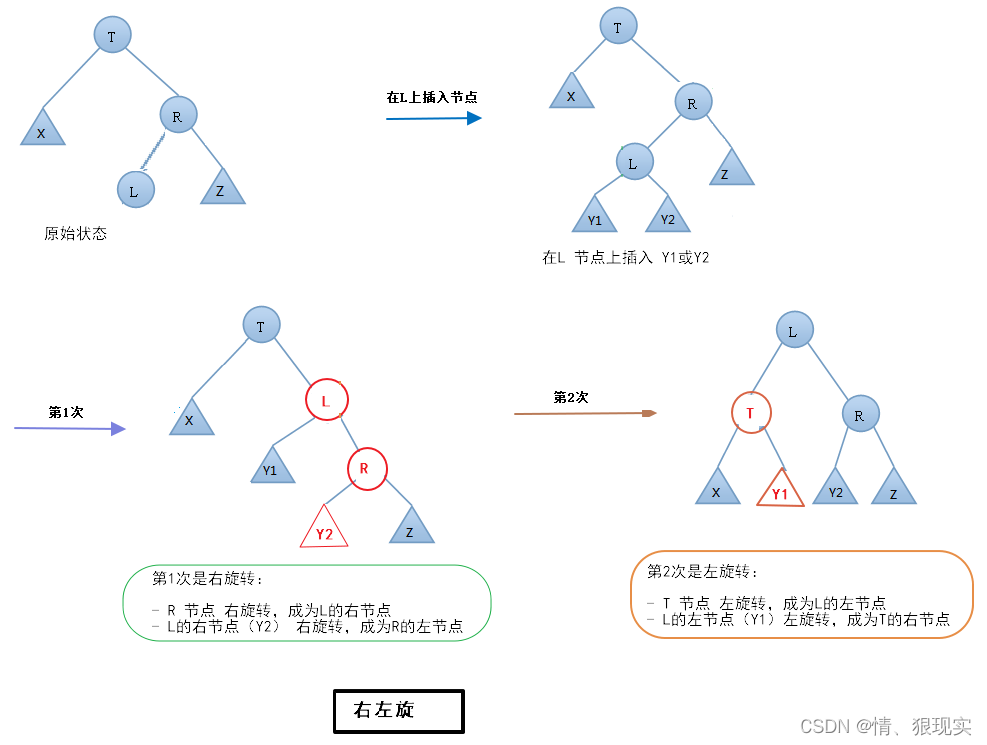
RL 右左旋 两次旋转步骤

1. 右旋转
   • R节点 右旋转，成为L的右节点
   • L的右节店(Y2)右旋转，成为R的左节点（右子节点右转）
2. 左旋转
   • T节点 左旋转，成为L的左节点
   • L的左节点(Y1)左旋转，成为T的右节点（左子节点左转）

旋转中心是根节点T的右节点（L）

ALV树删除元素

删除步骤

1. 寻找删除目标
2. 判断删除目标类型，使用转换思路，将其转换为删除叶子
3. 将删除元素目标与AVL树链接断开，调整平衡，完成删除

寻找删除目标

AVL树在搜寻删除目标的过程中，需要存储这条路径上的所有节点，以供后续回溯调整时使用。

Node parent = null;
Node p = t,  q = null;
Stack<Node> st;
//p是指向AVL树的根节点的一个指针
while (p) {		
	if (p.val == key)//当前节点就是删除目标
		break;
	parent = p;
	st.push(parent);//存储轨迹
	if (key > p.val)//删除目标在右树
		p = p.right;
	else//删除目标在左树
		p = p.left;
}
//执行到此处，p要么为预想的删除目标，要么为null（即不存在）
//下一步应该是判断删除目标的类型，进行转化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

判断删除类型，进行转化

删除目标存在两个子树或者子节点

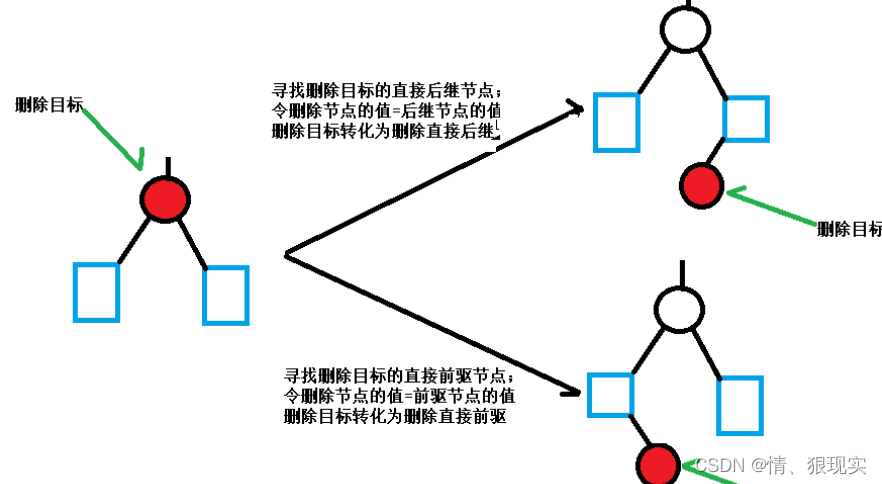
找到前驱或后驱节点，将值换成前驱或后驱节点值，最后替换掉该前驱或后驱节点

利用转化思想将非叶子节点转化为删除叶子节点，难度大大降低。

删除目标最多只有一个子节点

只有一个子节点，非常容易处理，我们只需要令删除目标的父节点链接删除目标的子节点，再删除目标即可。如下图所示：

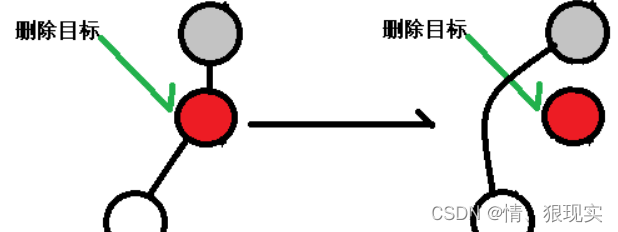
当然在这里面存在一种较特殊的情况，即整棵树只有两个节点，且删除目标是根节点。这种情况下我们直接令子节点成为根节点即可。如下：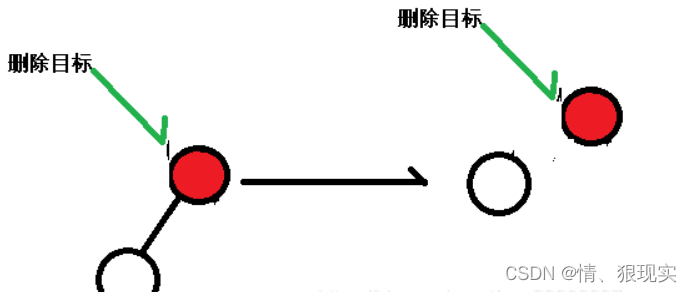

if (p==null)//删除目标不存在
	return false;
//删除节点
if (p.left && p.right) {//删除目标左右皆有
	parent = p;
	q = p.left;
	st.push(parent);
	while (q.right) {
		parent = q;
		st.push(parent);
		q = q.right;
	}
	p.val = q.val;
	p = q;//转化为删前驱
}
//p是删除目标,q是删除目标的子女节点
if (p.left)
	q = p.left;
else
	q = p.right;
if (parent==null)//删除目标是整棵AVL的根节点
	t = q;
else {
	//断开p节点，链接它的子女q
	if (parent.left == p) //删除目标是左孩子
		parent.left = q;
	else//删除目标是右孩子
		parent.right = q;
}
//下一步应该是调整平衡

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

调整平衡

上文可以得出本文在代码中是定义p为删除目标，因此下文沿用。

首先，我们应明白的是：

1. 若p是其父节点parent的左子女，删除p，引起左树高度降低，因此parent的平衡因子需要+1；
2. 若p是其父节点parent的右子女，删除p，引起右树高度降低，因此parent的平衡因子需要-1；
3. 因为parent的父节点也会受parent的影响，因此有可能也需要调整，所以有可能这个调整需要不断往上追溯。

parebt的平衡因子原来为0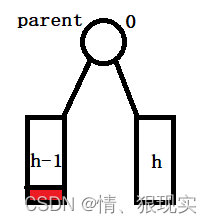

这种情况下，无论删除parent的左子树还是右子树上的节点，但是不会影响到以parent为父节点的子树高度，因此这种情况下只需要改变parent的平衡因子即可:0------>1/-1

parent的平衡因子原来绝对值为1，且被删节点位于较高的子树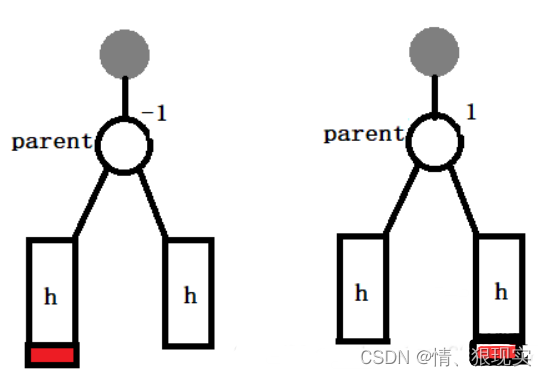

可以发现，该种情况下，删除支树上的节点将使得parent的平衡因子变为0。但由于删除使得该支树高度减1，因此需要向上平衡，沿着栈中存储的路径回溯。

因此，父节点平衡因子改动后并不意味着完成了平衡，而要追溯修改更上层的祖先节点。

parent的平衡因子原来绝对值为1，且被删节点位于较矮的子树

在这种情况下，删除较矮子树上的节点，parent的平衡因子会变为2/-2，parent失衡，光是调整平衡因子已经不能解决问题，而是需要旋转操作进行再平衡。

情况1：
parent的平衡因子为2，q的平衡因子为0，执行一次左单旋即可结束平衡工作；反之，parent的平衡因子为-2，q的平衡因子为0，执行一次右单旋即可结束平衡工作；

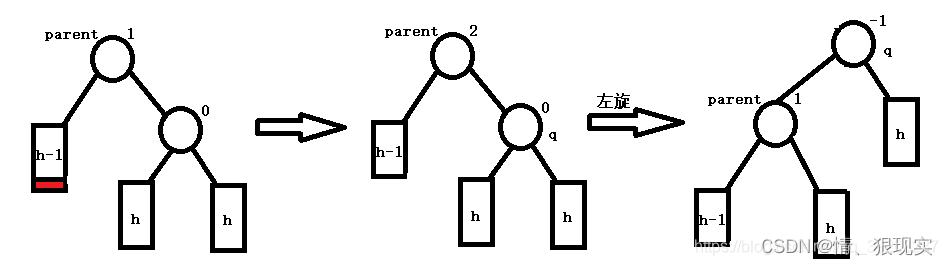
情况2：
parent的平衡因子与q的平衡因子同符号，则可以使用一个单旋转进行再平衡。如下图所示，二者皆为正，进行一次左旋即可平衡目前的支树结构。但由于旋转导致parent的父节点高度减1，所以需要继续向上考察路径中的平衡状态。

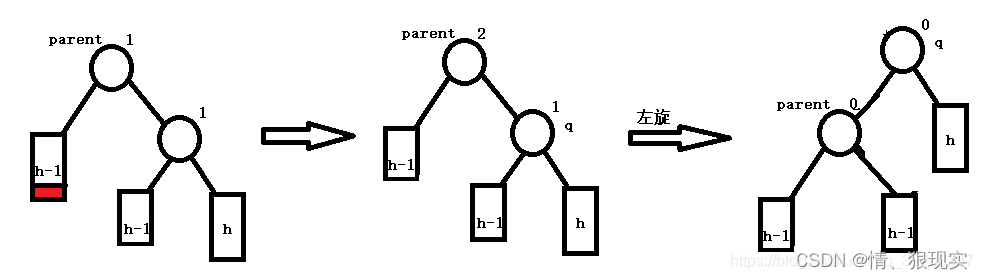
情况3：
parent的平衡因子与q的平衡因子异符号，则需要使用双旋转进行再平衡。但由于旋转导致parent的父节点高度减1，所以需要继续向上考察路径中的平衡状态。

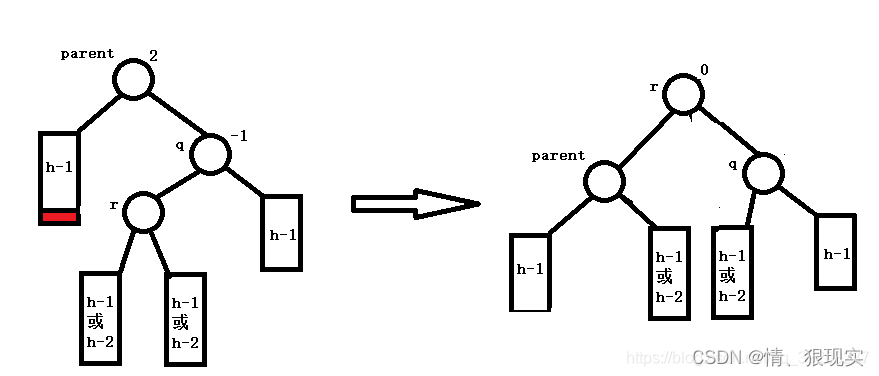
参考文章

数据结构 —— 图解AVL树(平衡二叉树)

易百教程-数据结构-AVL树

AVL树的删除