🔥快速排序

📖 1、图解算法

快速排序又叫quick sort，是一种比较高效的排序算法，其核心思想可以理解为是结合了分治法的排序

其基本的算法思路为：

①、先选择一个基数，这个基数可以是数组任意一个元素。
②、设定两个指针，一个指针指向数组的头部，一个指针指向数组的尾部
③、首先让尾指针向左移动，移动的条件是：如果左边的元素大于或等于基数，继续移动，否则，停止移动
④、当第三步的尾指针停止移动时，头指针才开始向右移动，如果右边的元素小于或等于基数，继续移动，否则，停止移动
⑤、如果头指针与尾指针都停止移动，而且两个指针没有相遇，则交换两个指针所指向数组的值，然后在现在的位置上继续重复第③、④、⑤步
⑥、最终，当两个指针发生相遇的时候，交换相遇处的值与基数的值，此时一轮排序结束
⑦、一轮排序结束后，此时基数被替换到了某个位置，假设为 i 位置，此时可以发现 i 左边的所有数都小于i所指向的数组值，同理 i 右边的都大于
⑧、此时将i左边和i右边的区域划分为两个子数组，继续重复上面的步骤，直到所有子序列都经过排序。
⑨、最终完成所有，数组排序成功。
值得一提的是，如果是数组从小到大排序，则比基数小的数放左边，比基数大的数放右边，如果是从大到小排序，则相反即可。

看上去有点复杂，没事，下面直接开始最通俗易懂的图解方法：
排序数组 [0,0,2,3,2,1,2,4]，排序方式：递增排序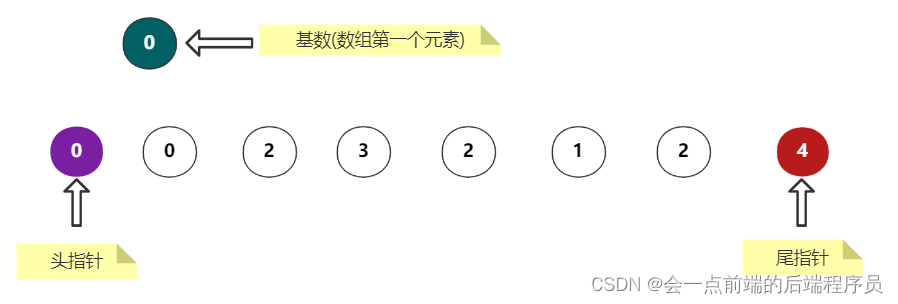

第一步，先让尾指针向前移动，直到找到第一个小于基数的数或者与i重合的时候才停止
很明显结果如下，停止的条件是i 和 j 重合了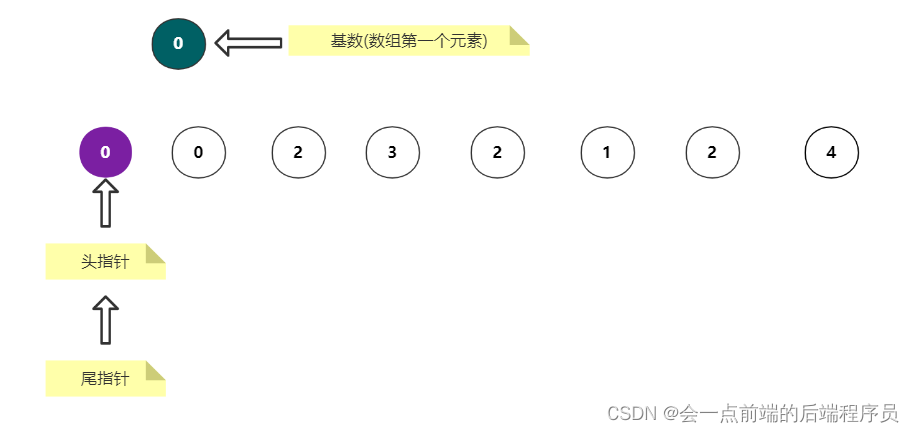

由于两个指针发生了相遇，所以此时应该交换相遇处的值与基数的值，发现基数值与 相遇的值是同一个位置的值，则忽略交换（因为此时交换没有任何意义）
接下来，划分子数组区域继续排列
此时 i = 0，j = 0 ，而划分区域的公式为: (len是原数组长度，而且此时 i 必然等于 j)
$$左边子区域[0,i-1]，右边的子区域[i+1,len-1]$$
划分的结果 $$左边子区域:[]，右边的子区域:[0,2,3,2,1,2,4]$$

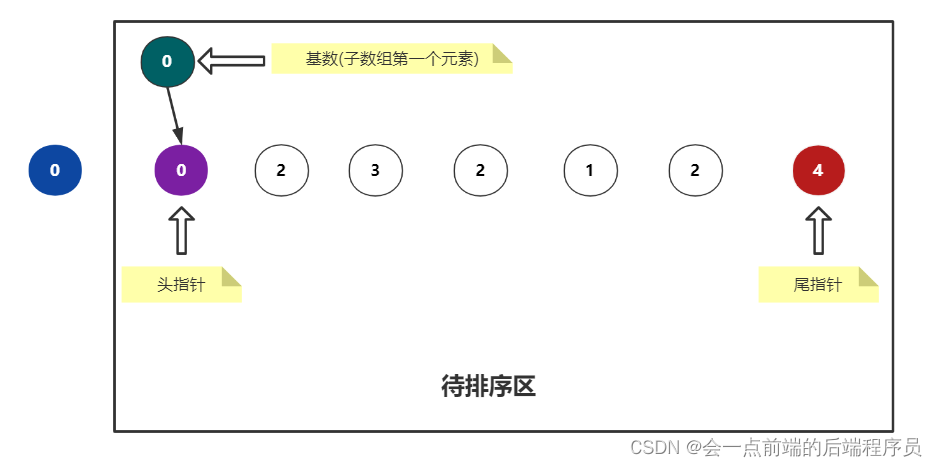
按照上面的方法，不难看出此时的排序结果为如下

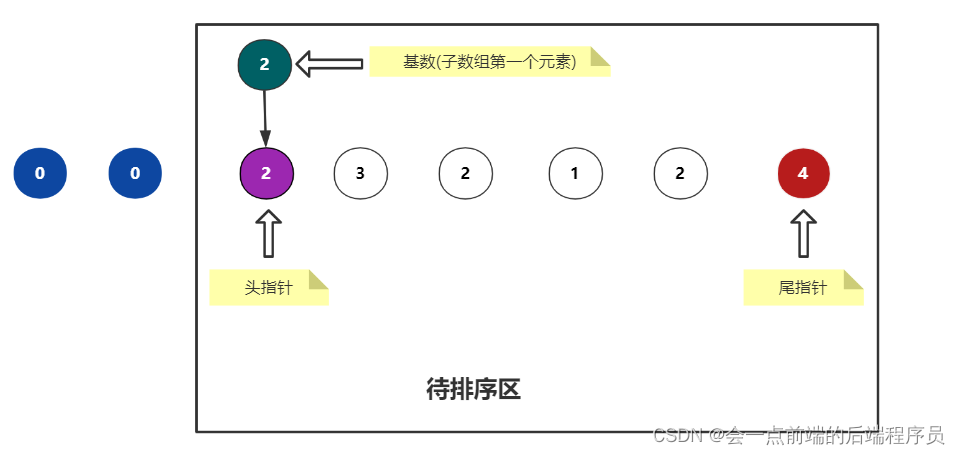
此时的排序结果我们就需要注意一下了，跟上面两种方法的排序结果不一样
首先尾指针左移，第一个小于基数的元素是1，此时 j 停下来不动
然后头指针右移，第一个大于基数的元素是3，此时 i 停下来不动
如下结果


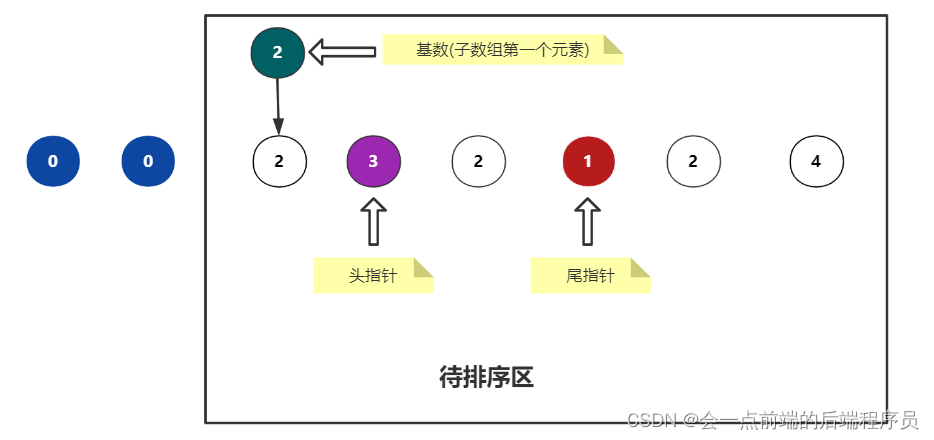
可以看到，此时的 i 与 j 并没有发生碰撞，怎么办呢，交换i和j的元素即可，交换后如下

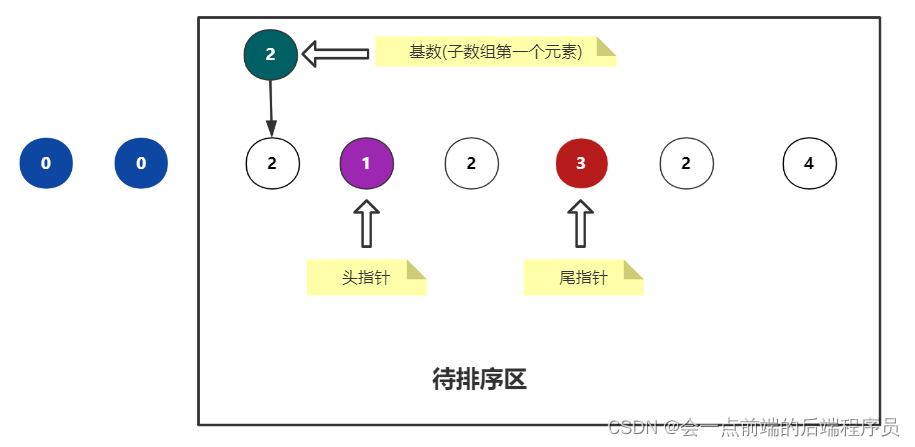继续让重复下面操作
首先尾指针左移，第一个小于基数的元素是1，此时 j 停下来不动
i 与 j 已经发生了碰撞，此时 i 不需要移动

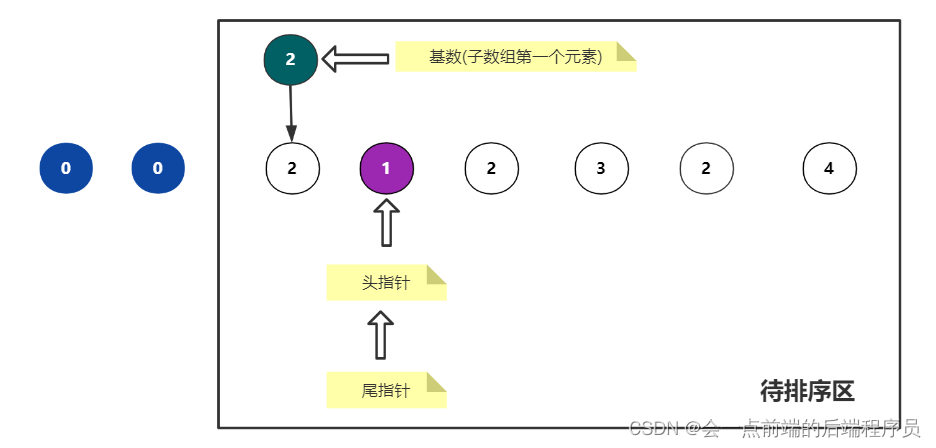
交换 i上的数与基数

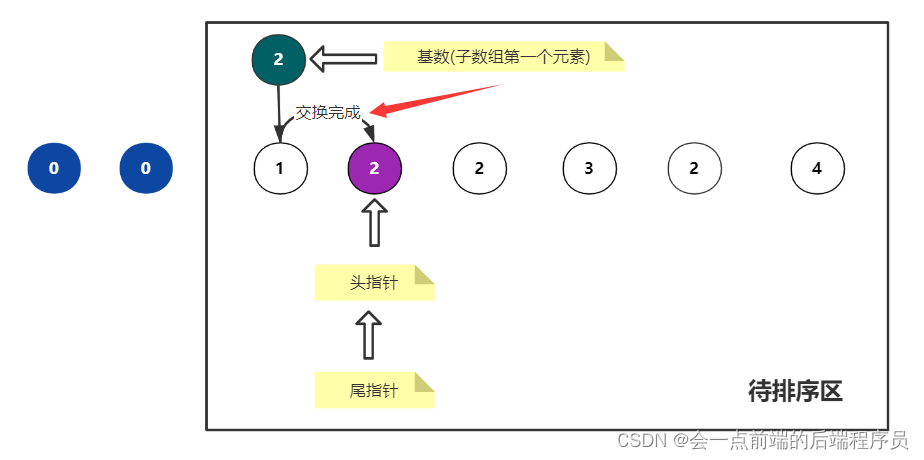
到这里，这一轮就交换完成了，下面我们继续在这个子数组的基础上再划分左右子数组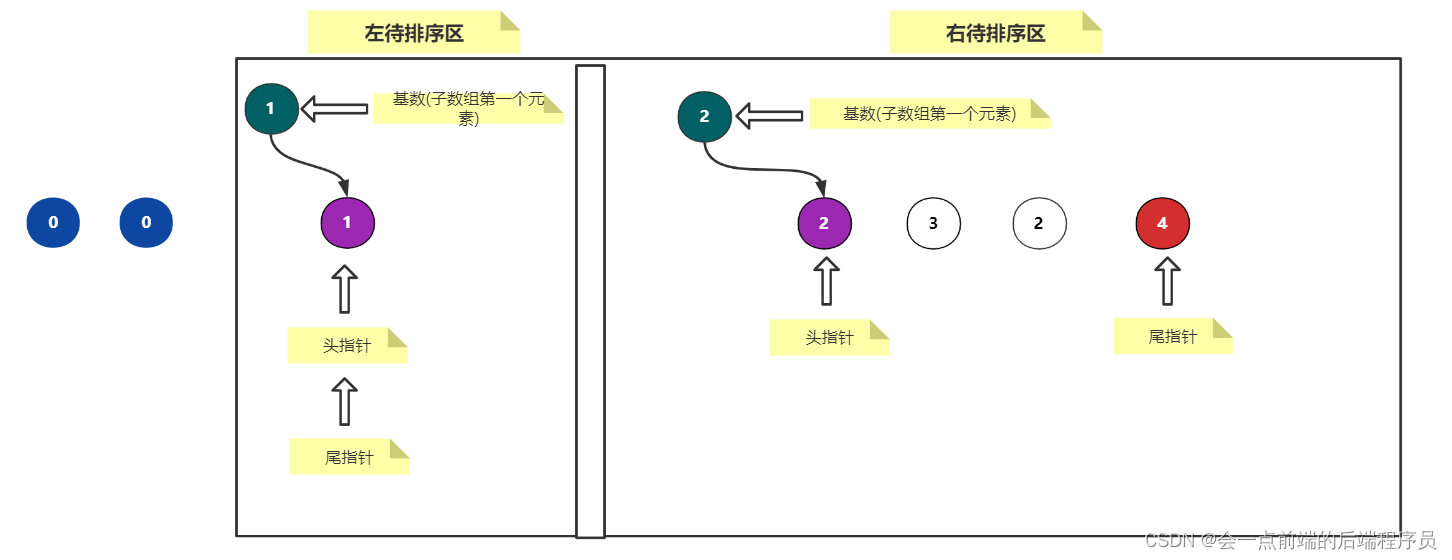

到这里相信大家差不多都了解了，有限划分左右子区，一直迭代下去，是一个递归的过去
接下来的步骤大家可以手动自己试试！ O(∩_∩)O哈哈~

C#与Sql连接字符串的公用类 DBHelper

txt 4星 超过85%的资源 1KB

下载

到处，快速排序的演示就结束了 😄

📖 2、算法代码

c++代码如下

// 快速排序
// arr 是数组， start 是子数组的起始位置，end 是子数组的结束位置，[start，end]
void get_partition(vector<int>& arr, int start,int end){
    if(start >= end) return;     
    int base = start, i = start,j = end;
    while(i < j){
        while(i < j && arr[j] >= arr[base]) --j;
        while(i < j && arr[i] <= arr[base]) ++i;
        if(i < j){
            swap(arr[i],arr[j]);
        }
    }
    swap(arr[base], arr[i]);
    get_partition(arr, start, i - 1);
    get_partition(arr, i + 1, end);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

📖 3、例题

剑指offer 40——最小的k个数

这道题目虽然最优解不是快速排序（其实是快速选择或者堆排序？？？），但是用快速排序可以练练手感。
but，我感觉，快速选择和快速排序在这道题目里面时间相差不大

我提交的 c++ 代码

快速排序
36ms

class Solution {
public:
    // 快速排序
    void get_partition(vector<int>& arr, int start,int end){
        if(start >= end) return;     
        int base = start, i = start,j = end;
        while(i < j){
            while(i < j && arr[j] >= arr[base]) --j;
            while(i < j && arr[i] <= arr[base]) ++i;
            if(i < j){
                swap(arr[i],arr[j]);
            }
        }
        swap(arr[base], arr[i]);
        get_partition(arr, start, i - 1);
        get_partition(arr, i + 1, end);
    }

    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> c;
        if(arr.size() == 0 || k == 0) return c;
        get_partition(arr,0,arr.size()-1);
        return vector<int>(arr.begin(),arr.begin() + k);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

自己写的堆排序，很低效哈哈哈，因为没有考虑维护堆内元素的数量 k
1768ms

class Solution {
public:
    // 已经排好的个数为k，默认为0
    // 小跟堆排序
    void heapify(vector<int>& arr,int k, vector<int>& res){
        int len = arr.size() - k;
        int flag = 0;
        for(int i = (len >> 1) - 1; i >= 0; --i){
            flag = 0;
            if(arr[i] > arr[(i << 1) + 1]){
                flag = 1;
            }
            if(
                    ((i+1) << 1) < len 
                    && arr[i] > arr[(i+1) << 1] 
                    && arr[(i << 1) + 1] > arr[(i+1) << 1] 
                )
            {
                flag = 2;
            }
            if(flag == 1){
                swap(arr[i], arr[(i << 1) + 1]);
            }else if(flag == 2){
                swap(arr[i], arr[(i+1) << 1]);
            }
        }
        res.push_back(arr[0]);
        swap(arr[0],arr[len-1]);
    }
    
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> res;
        if(arr.size() == 0 || k == 0) return res;
        // 将 arr 看作是一个堆
        int count = 0;
        while(k--){
            heapify(arr, count++, res);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

STL库的 nth_element函数
16ms

class Solution {
public:

    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        nth_element(arr.begin(),arr.begin()+k,arr.end());
        return vector<int>(arr.begin(),arr.begin() + k);
    }
};
1
2
3
4
5
6
7
8

📖 4、时空复杂度分析

最好的情况，时间复杂度为 $O(n\ast {\log }_{2}n).$

最坏的情况，刚好和你排序相反，每趟都要交换，时间复杂度即为 $O(n^2).$

无任何大容量额外空间，所以空间复杂度为 $O(1).$