-
self-attention学习笔记
1.引入Slef-Attention的原因
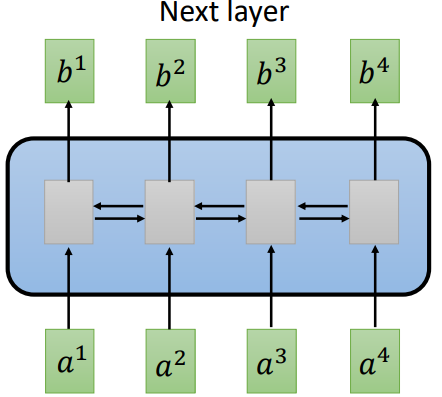
在自然语言处理中,使用RNN(这里指的的是LSTM)处理输入输出数据的时候,LSTM可以解决长文本依赖,因为他可以依赖于前面的文本,且不能够做并行计算,导致运算的速度非常慢。
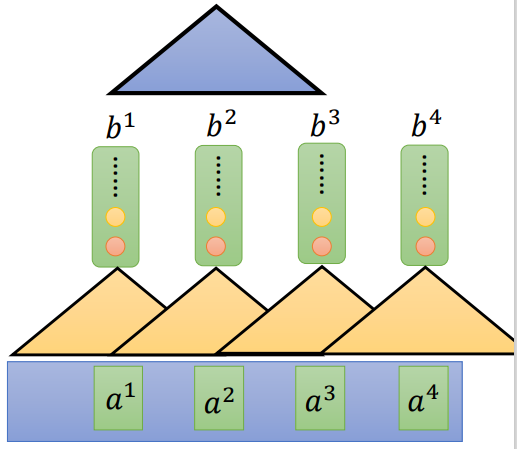
所以有很多学者就会使用CNN去替代RNN,CNN需要叠加许多层,就可以看到所有的序列信息,并且可以并行计算。但是存在一个问题,就是需要叠加很多层,这样也间接的导致了效率变低。
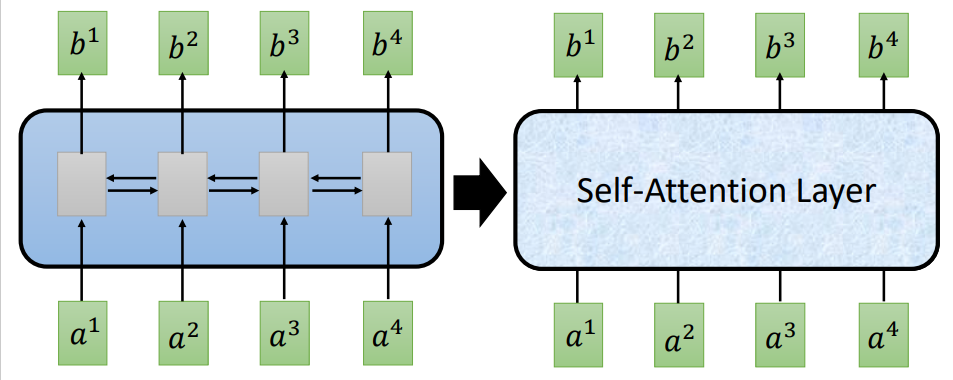
所以引入的self-attention机制,就可以解决这两个问题:- 1.看到每一个节点对所有节点的依赖
- 2.可以进行叠加运算
如右图所示,b1可以依赖于a1,a2,a3,a4,b2也是如此。
2.self-attention原理讲解
2.1大致原理讲解
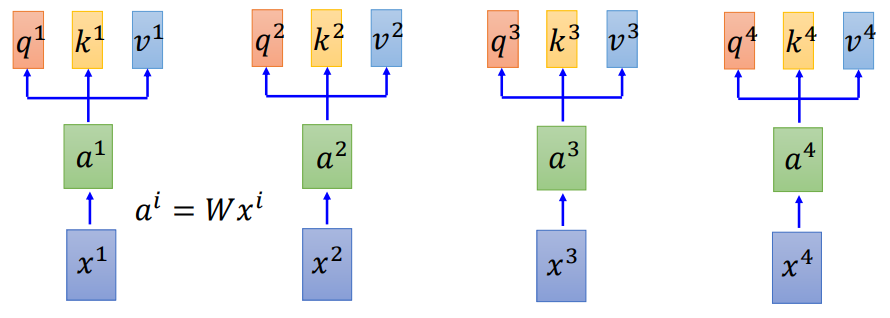
- 1.计算a
x1,x2,x3,x4会乘上一个矩阵W得到a1,a2,a2,a3。 - 2.计算q,k,v
通过a与一个矩阵w计算可以得到q,k,v,三个值
其中每个值的作用和计算过程如下:
q:query(用于去匹配其他值的), qi=Wqai
k:key(用于被匹配), ki=Wkai
v:抽取的信息, vi=Wvai - 3.计算
α
\alpha
α
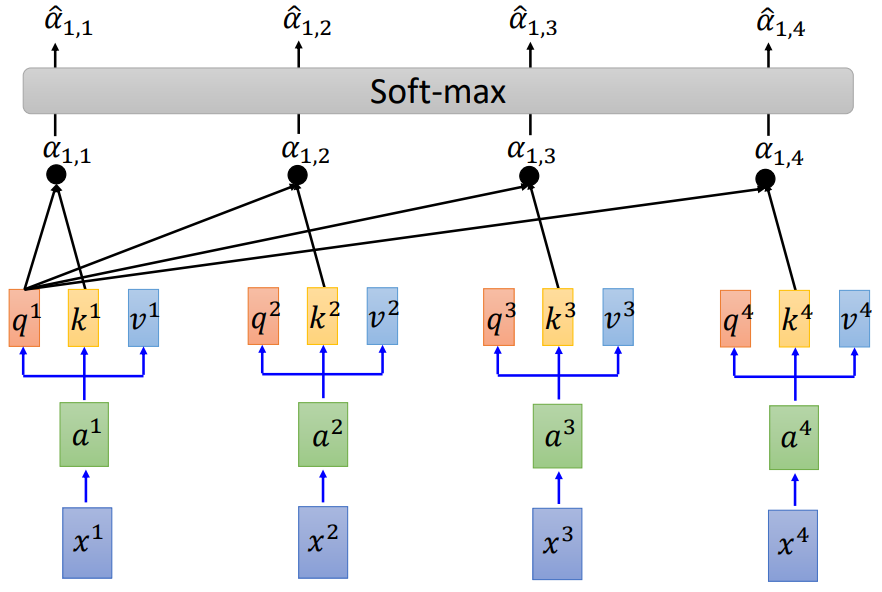
那每一个query q去对每一个key k做attention,其实就是q1与ki做点乘计算
其中: α \alpha α1,i=q1ki d \sqrt{d} d - 4.计算
α
^
\widehat{\alpha}
α
这个算法就是将所有的 α < s u b > 1 , i < / s u b > \alpha1,i α<sub>1,i</sub>相加在一起,然后进行一个soft-max输出,得到每一个 α \alpha α的概率分布。
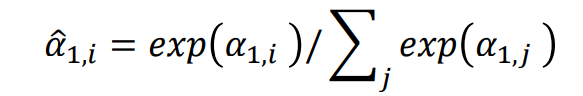
- 5.计算b
将的 α ^ \widehat{\alpha} α 与每个vi做一个点乘,然后再相加,就得到了b,也就最终的输出。
这整个过程就是self-attention机制,计算每个节点与其他节点之间的依赖.
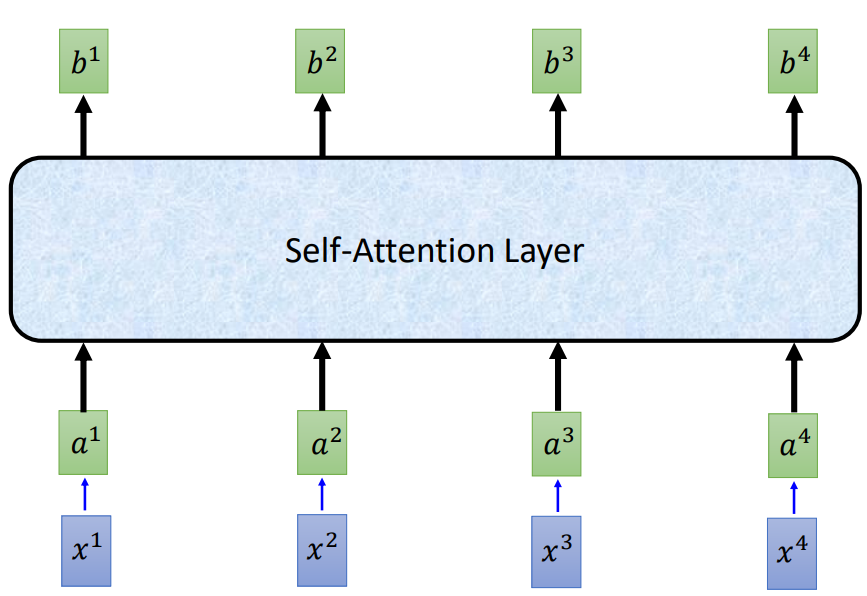
2.2 数学计算方式
- q,k,v的矩阵计算
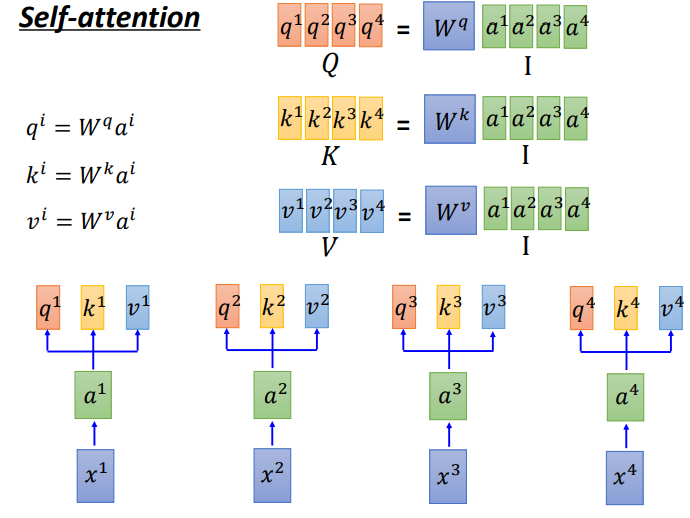
因为q是wq与每一个a进行点乘得到的,所以可以把所有的a看做一个矩阵,就是wq与a矩阵计算的结果,这样就达到了并行计算了.
k,v的计算过程也是如此. - 计算
α
\alpha
α
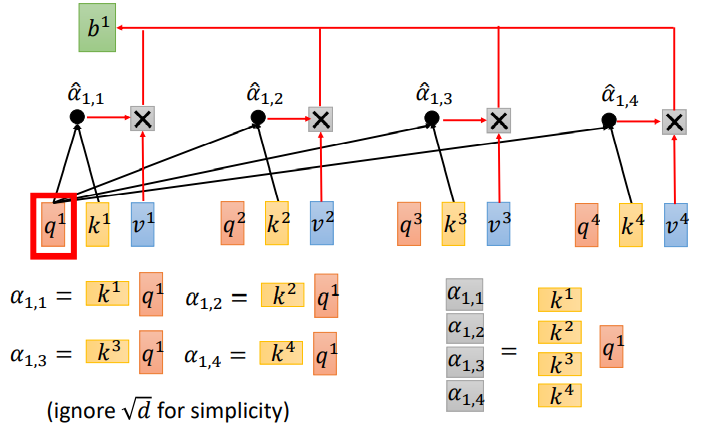
α \alpha α是由q1与每一个k计算的结果(忽略 d \sqrt{d} d),所以可以把所有的k看做一个矩阵,这样就是k矩阵与q的矩阵计算. - 计算
α
^
\widehat{\alpha}
α
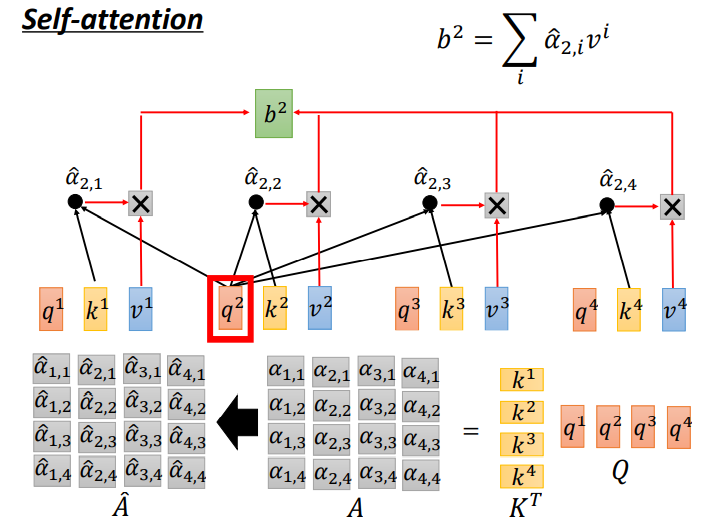
把之前计算的 α \alpha α放入一个soft-max函数得到 α ^ \widehat{\alpha} α - 计算b
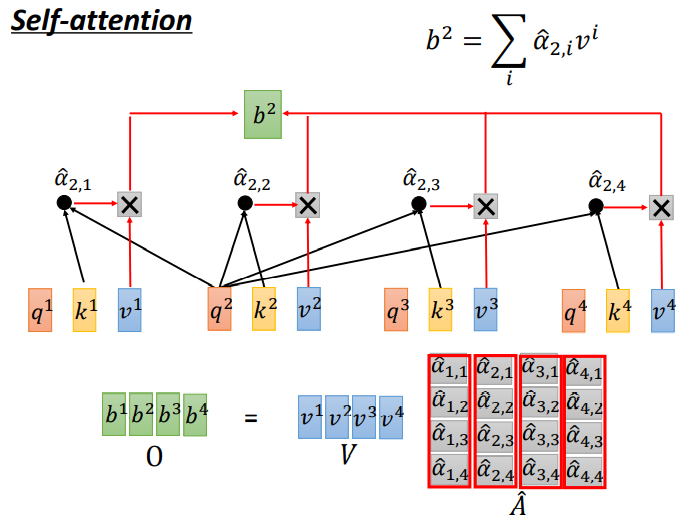
将 α ^ \widehat{\alpha} α 与v矩阵做点乘,然后把所有点乘的结果相加就得到了b
整个过程抽象化如下图所示:
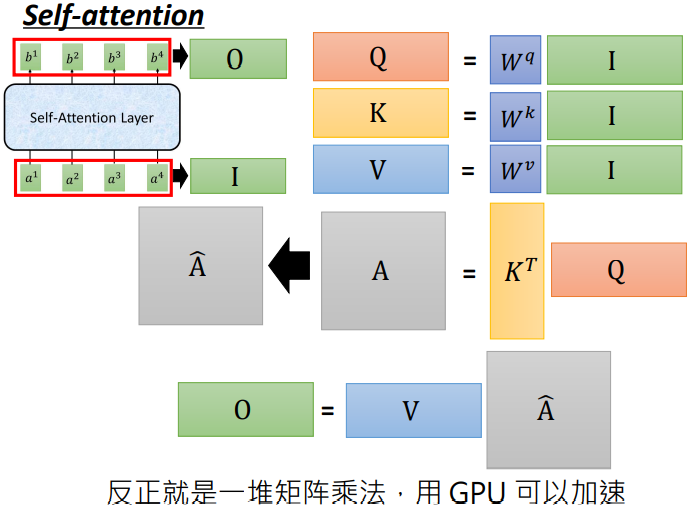
-
相关阅读:
b树(一篇文章带你 理解 )
揭秘 · 机器人酒店
基于数学模型水动力模拟、水质建模、复杂河网构建技术在环境影响评价、排污口论证及防洪评价中的实践技术应用
软件测试基本概念(1)
MTK OEM解锁步骤
Servlet概述及接口
使用微信公众号搭建免费查券返利机器人来赚佣金详细教程分享
docker login harbor http login登录
详解Native Memory Tracking之追踪区域分析
苹果启动2024年SRDP计划:邀请安全专家使用定制iPhone寻找漏洞
- 原文地址:https://blog.csdn.net/qq_35653657/article/details/126003476