【左神算法笔记】Class2,3 各种排序算法总结

1.时间复杂度为O(n^2)的排序

选择排序
时间复杂度：O(n^2)
空间复杂度： O(1)
不稳定

// 简单选择排序，时间复杂度O(n^2)，不稳定
void SelectSort(int arr[],int n)
{
	for (int i = 0; i < n; i++)
	{
		int min = arr[i];
		int minIndex = i;
		for (int j = i + 1; j < n; j++)
		{
			if (arr[j] < min)
			{
				min = arr[j];
				minIndex = j;
			}
		}
		if (minIndex != i)
		{
			int temp = arr[i];
			arr[i] = arr[minIndex];
			arr[minIndex] = temp;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

冒泡排序
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定

//冒泡排序，时间复杂度O(n^2)，稳定
void BubbleSort(int arr[], int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = i + 1; j < n; j++)
		{
			if (arr[i] > arr[j])
			{
				int temp = arr[i];
				arr[i] = arr[j];
				arr[j] = temp;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

插入排序
时间复杂度O(n^2)
空间复杂度O(1)
稳定

//插入排序，时间复杂度O(n^2),稳定
void InsertSort(int arr[], int n)
{
	for (int i = 1; i < n; i++)
	{
		int ivalue = arr[i];
		bool isInsert = false;
		for (int j = i - 1; j >= 0; j--)
		{
			if (arr[j]>ivalue)
				arr[j + 1] = arr[j];
			else
			{
				arr[j + 1] = ivalue;
				isInsert = true;
				break;
			}
		}
		if (!isInsert)
		{
			arr[0] = ivalue;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

2.时间复杂度为O(nlogn)的排序

堆排序
时间复杂度为O(nlogn)
空间复杂度为O(1)
不稳定
堆排序就一个数组自己在玩移动的过程，不需要额外空间存储，所以空间复杂度为O(1)

首先明确，堆的结构就是用数组实现的完全二叉树结构
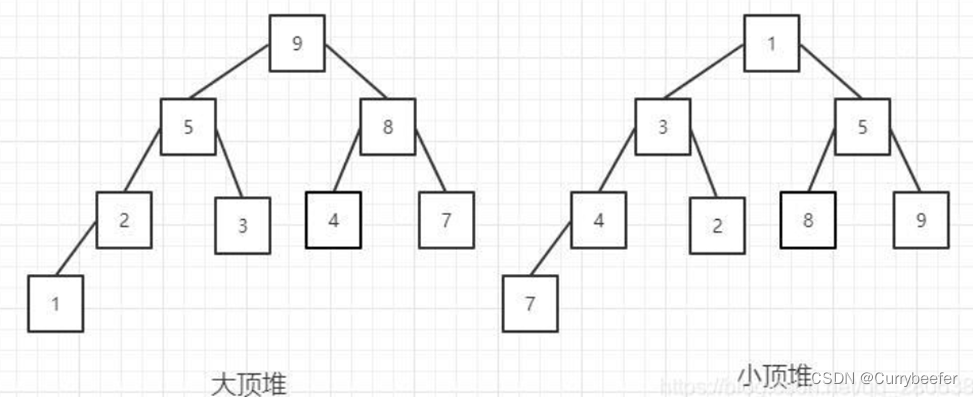对于任意一个节点在数组中下标为i，则
父节点：(i-1)/2
左孩子：2i+1
右孩子：2i+2

堆有两种操作，分别是上浮和下沉，这里以大顶堆为例
上浮：若一个节点比父节点大，则交换两者位置，这个节点在堆中就上升

//上浮
void HeapInsert(int arr[], int index)
{
	//arr[index]是当前的数，arr[(index-1)/2]是index的父位置的数
	//若当前节点值比父位置的值大，则交换两个节点的值，反复循环，让节点不断上浮
	while (arr[index] > arr[(index - 1) / 2])
	{
		SwapArr(arr, index, (index - 1) / 2);
		index = (index - 1) / 2;
	}
}
1
2
3
4
5
6
7
8
9
10
11

下沉：如果一个节点比子节点大，则交换两者位置，让这个节点在堆中往下沉

//下沉
void MaxHeapify(int arr[], int start, int end)
{
	//start代表需要调整的节点
	//end表示当前大顶堆的最后一个节点的下标位置

	int dad = start;
	int son = dad * 2 + 1;//这里son是初始节点的左孩子
	while (son <= end)
	{
		//如果右孩子的值比左孩子大，那么son=右孩子，因为要找到子节点中最大的那个和父节点交换
		if (son + 1 <= end && arr[son] < arr[son + 1])
			son++;
		if (arr[dad] > arr[son])//如果父节点大于两孩子中最大的那个，那就没什么事了，返回
			return;
		else
		{
			//否则交换这父子两个节点的值
			SwapArr(arr,0,i);
			//继续往下遍历，因为父节点现在在子节点上，其值可能会比子节点的子节点（孙子节点）小，需要继续往下检查，直到end结束
			dad = son;
			son = dad * 2 + 1;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

堆排序的思路就是

1. 先将数组构造成大顶堆
2. 取堆顶的元素，于数组最末尾（堆的最后一个节点）互换，此时数组最尾巴的那个元素就是之前堆顶的元素，也就是最大的那个元素。那么就不用动了，放在那里。然后堆的大小-1。
3. 接下来得把堆顶的那个元素通过下沉操作放到堆合适的位置去，这样又构造出了一个大顶堆，如此反复。

那么看代码

void HeapSort(int arr[], int len)
{
	//将给定的数组先调整成一个大顶堆  复杂度：O(nlogn)
	for (int i = 0; i < len; i++)
		HeapInsert(arr, i);//O(logn)

	//初始化结束后，就可以将堆顶的元素与最后一个节点交换，交换后最后一个节点就被排除在二叉堆外了 复杂度：O(nlogn)
	for (int i = len - 1; i > 0; i--)
	{
		swap(arr[0], arr[i]);
		//然后由于堆顶元素变化了，那么我们就需要继续调整，重新构造一个大顶堆，直到结束
		MaxHeapify(arr, 0, i - 1);//O(logn)
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

但是实际上，在初始化的时候我们只需要构造一个大顶堆就好了，那其实我们有更快的办法来构造。只需要从堆的末尾节点开始，不断执行下沉操作，这样比从顶部开始遍历然后上浮会快一些。那么如果这样写，第一步的时间复杂度会变为O(n)。

【面试必备】排序、查找算法总结

application/pdf 3星 超过75%的资源 239KB

下载

第一种是从下标为0开始逐个insert，每次insert是logN的时间复杂度，N个元素为N*logN的时间复杂度。第二种是将每个元素做heapify处理（与之前插入0位置的额heapify不同），最低一层的叶子节点可以不做处理。倒数第二层的节点占N/4，最多需要做一次交换，倒数第三层的最多做两次交换，这是一个等比乘等差的求和，最终的结果是O（N）的时间复杂度。

void HeapSort(int arr[], int len)
{
	//初始化二叉树，从第一个非叶子节点开始调整整个树
	for (int i = len - 1; i >= 0; i--)//O(n)
		MaxHeapify(arr, i, len - 1);

	//初始化结束后，就可以将堆顶的元素与最后一个节点交换，交换后最后一个节点就被排除在二叉堆外了 复杂度：O(nlogn)
	for (int i = len - 1; i > 0; i--)
	{
		swap(arr[0], arr[i]);
		//然后由于堆顶元素变化了，那么我们就需要继续调整，重新构造一个大顶堆，直到结束
		MaxHeapify(arr, 0, i - 1);//O(logn)
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

快速排序
时间复杂度：O(nlogn)
空间复杂度：O(logn)
不稳定
如果每次划分都能在中点划分的话，根据master公式，可以算出时间复杂度为O(nlogn)，但是不可能每次都能划分在中点位置，所以这是最好情况。而时间复杂度是考虑最坏情况的。

快排这里给出了三个版本
快排1.0 每次选取最后一个数字作为基准。最坏复杂度为O(n^2)，因为存在人为构建最坏情况
快排2.0 每次可以划分出小于等于大于三个区域，如<5 ==5 >5，每次搞定一批数字。最坏复杂度为O(n^2)，因为还是存在人为构建最坏情况
快排3.0 随机选择的一个数，与最尾巴数字交换，并以这个新的尾巴数字为基准做划分，这样就无法人为构建最差情况，这样时间复杂度就是O(nlogn)

快排3.0算法如下

void QuickSort3(int arr[], int L, int R)
{
	if (L < R)
	{
		SwapArr(arr, L+(int)(rand()%(R-L+1)),R);
		int* p = Partition(arr, L, R);
		QuickSort3(arr, L, p[0] - 1);
		QuickSort3(arr, p[1] + 1, R);
		delete[] p;
	}
}

int* Partition(int arr[], int L, int R)
{
	//arr[R] 是比较的基准数
	int less = L - 1;//less是<区的下标
	int more = R;//more是>区的下标,现在>区包含了基准数arr[R]这一个元素
	int i=0;//指针
	while (i < more)//当指针与>区重合时停止
	{
		//当前数比基准数小，与<区后的第一个元素互换，然后扩大<区将这个数包含进来，指针指向下一个元素
		if (arr[i] < arr[R])
		{
			SwapArr(arr, less+1, i);
			less++;
			i++;
		}
		else if (arr[i] > arr[R])//当前数比基准数大，与>区前第一个元素交换，移动>区域吞并这个数，指针不动
		{
			SwapArr(arr, more-1, i);
			more--;
		}
		else//如果等于基准数，什么都不做，指针移动
			i++;
	}
	SwapArr(arr, more, R);//交换基准数和more的第一个元素区域
	return new int[] {less + 1, more};//返回等于区域的下标始末
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

归并排序
时间复杂度：O(nlogn)
空间复杂度：O(n)
稳定

归并排序的时间复杂度是基于master公式算出来的，空间复杂度为O(n)，因为merge的时候需要借助额外数组完成

void RadixSort(int arr[],int n, int digit)
{
	const int radix = 10;//设数字为十进制
	int i = 0, j = 0;
	int *bucket = new int[n];//辅助数组桶

	for (int d = 1; d <= digit; d++)//d代表验证第几位，这里从1也就是从个位开始
	{
		int* count = new int[radix]();//count数组，这里加了()代表全部初始化为0
		for (i = 0; i < n; i++)//count数组用于计数，即统计arr中，d位为j的有几个
		{
			j = GetDigit(arr[i], d);
			count[j]++;
		}
		for (i = 1; i < radix; i++)//统计完毕，将count数组变为前缀和数组，count[i]此时代表d位小于等于i的有几个
			count[i] = count[i] + count[i - 1];

		for (i = n-1; i >= 0; i--)//从后往前遍历，将数字填写在bucket中，完成一次排序
		{
			j = GetDigit(arr[i], d);
			bucket[count[j] - 1] = arr[i];
			count[j]--;
		}
		for (i = 0, j = 0; i <n; i++, j++)//复制给arr
			arr[i] = bucket[j];

		delete[] count;
	}
	delete[] bucket;
}

int GetDigit(int num, int digit)
{
	int res = 0;
	for (int i = 0; i < digit; i++)
	{
		res = num % 10;
		num /= 10;
	}
	return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

桶排序（基数排序）
时间复杂度O(n)
空间复杂度O(m+n)

桶排序和之前说的排序不同，其是不是基于比较排序，时间复杂度是O(n)，不受O(nlogn)下限的影响。

在算法实现上，桶排序需要两个数组辅助，分别是count计数数组和bucket出桶数组。
由digit决定需要进行几次排序，每次排序过程中使用count数组统计对于数组当前位d的值中小于i的数量。然后出桶放入bucket中，视为一次排序。

/// 

/// 桶排序
/// 
/// 数组
/// 数组长度
/// 数组最高的位数
void RadixSort(int arr[],int n, int digit)
{
	const int radix = 10;//设数字为十进制
	int i = 0, j = 0;
	int *bucket = new int[n];//辅助数组桶

	for (int d = 1; d <= digit; d++)//d代表验证第几位，这里从1也就是从个位开始
	{
		int* count = new int[radix]();//count数组，这里加了()代表全部初始化为0
		for (i = 0; i < n; i++)//count数组用于计数，即统计arr中，d位为j的有几个
		{
			j = GetDigit(arr[i], d);
			count[j]++;
		}
		for (i = 1; i < radix; i++)//统计完毕，将count数组变为前缀和数组，count[i]此时代表d位小于等于i的有几个
			count[i] = count[i] + count[i - 1];

		for (i = n-1; i >= 0; i--)//从后往前遍历，将数字填写在bucket中，完成一次排序
		{
			j = GetDigit(arr[i], d);
			bucket[count[j] - 1] = arr[i];
			count[j]--;
		}
		for (i = 0, j = 0; i <n; i++, j++)//复制给arr
			arr[i] = bucket[j];

		delete[] count;
	}
	delete[] bucket;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

3.排序总结

选择排序：不稳定，做交换的时候就会改变次序

冒泡排序：稳定，遇到相同元素的时候不交换就好了
插入排序：稳定，一样，遇到相等的不交换就好了
归并排序：稳定，merge的时候遇到相等的，先拷贝左边的，就可以做到稳定
快排：不稳定，partition的时候做不到稳定

堆排序：当然不稳定，每次调整堆的时候就做不到稳定性
所有桶相关排序：计数排序和基数排序，可以稳定

目前没有找到时间复杂度在O(N*logN)以下的排序
目前没有找到时间复杂度在O(nlogn)且空间复杂度在O(n)以下的条件下能保证稳定的算法