主要内容

1. 梯度检测
2. 随机初始化
3. 神经网络算法步骤总结

一、梯度检测

• 在采用反向传播算法时很容易产生于一些小的 bug(程序错误)，当它与梯度算法或者其他算法一起工作时，看起来能正常运行并且代价函数也在逐渐变小，但最后的到的神经网络的误差会比无 bug 的情况下高出一个量级，这时采用梯度检测就能很好的避免这些问题

• 在每次使用神经网络或者其他复杂模型中实现反向传播或者类似梯度下降算法时，都建议做梯度检测

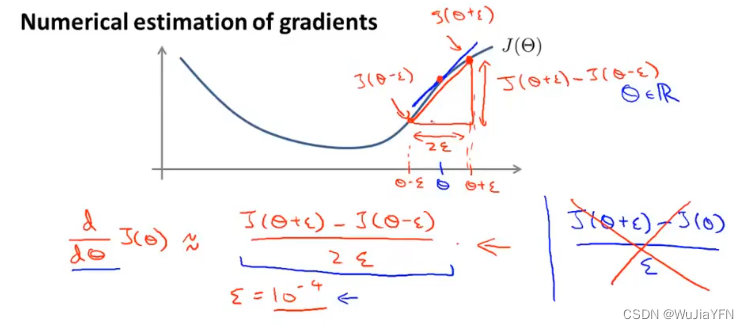
• 梯度检验的基本思想 是利用数学上的导数/偏导数的定义的思想，在2*ε很小的情况下，将两点连线的斜率近似等于中点的曲线斜率，由此验证在算法中计算得到的导数/偏导的准确性

• 在θ为实数的情况下，计算过程如下图：

• θ是向量的情况下，计算过程如下图：

  

  
  

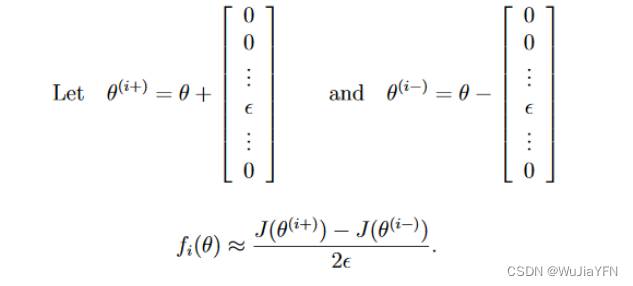
• 假设通过中值定理得到的梯度为approxgrad，经过反向传播得到的梯度为grad，如果满足以下等式，则说明反向传播得到的梯度精度还行。

  

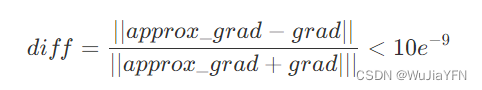
• 梯度计算正确的情况下，当算法进行学习的时候要关闭梯度检测，因为它非常耗时。

• 

二、随机初始化

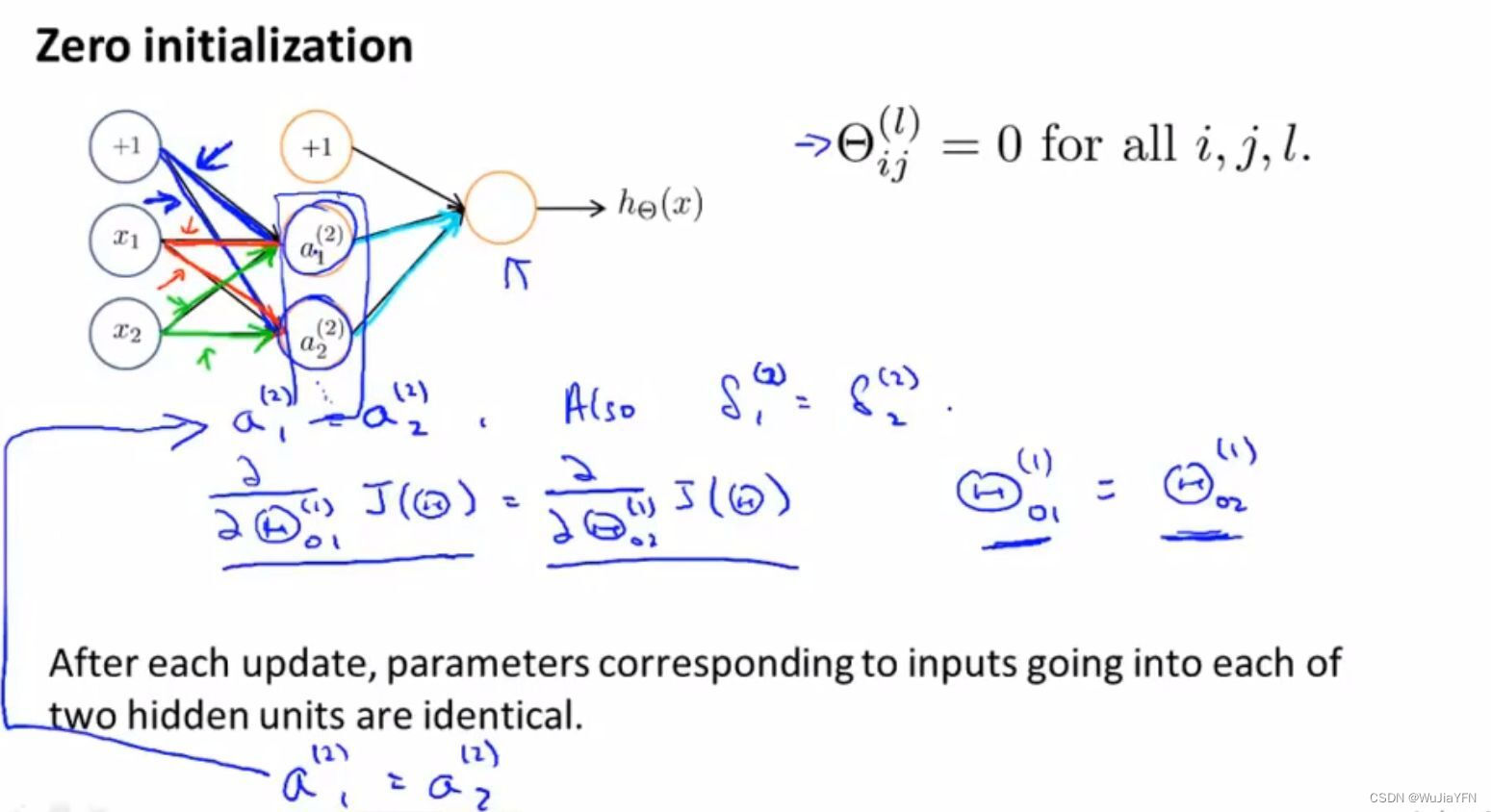
• 在之前的θ向量初始化采取的策略是：zero initializtion(对称权重问题 )，这样初始化会出现同层hidden unit完全对称，出现高冗余，权重都相同。

  

• 合理的应该采用随机初始化 的策略， 对于权重矩阵中的每一个θ，我们选用[-ε, ε]的均匀分布来初始化它。

  

三、神经网络算法步骤总结

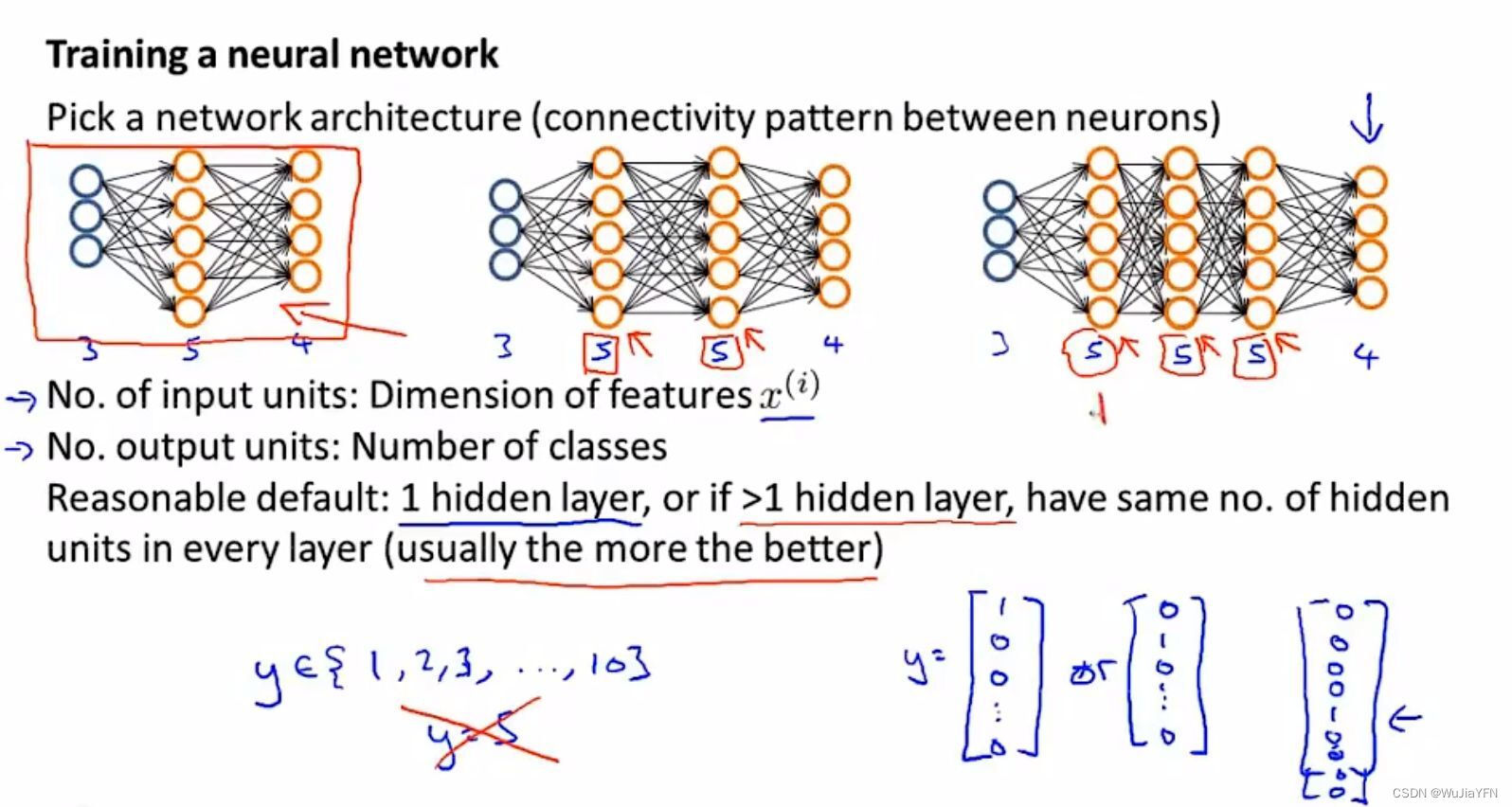
3.1 选择神经网络架构

• 选择每一层多少个隐藏单元以及多少个隐藏层。

• 输入层和输出层units由特征维度和分类个数决定。

• 注意输出矩阵y需要写成成向量形式 as [1 0 0 …]T

  

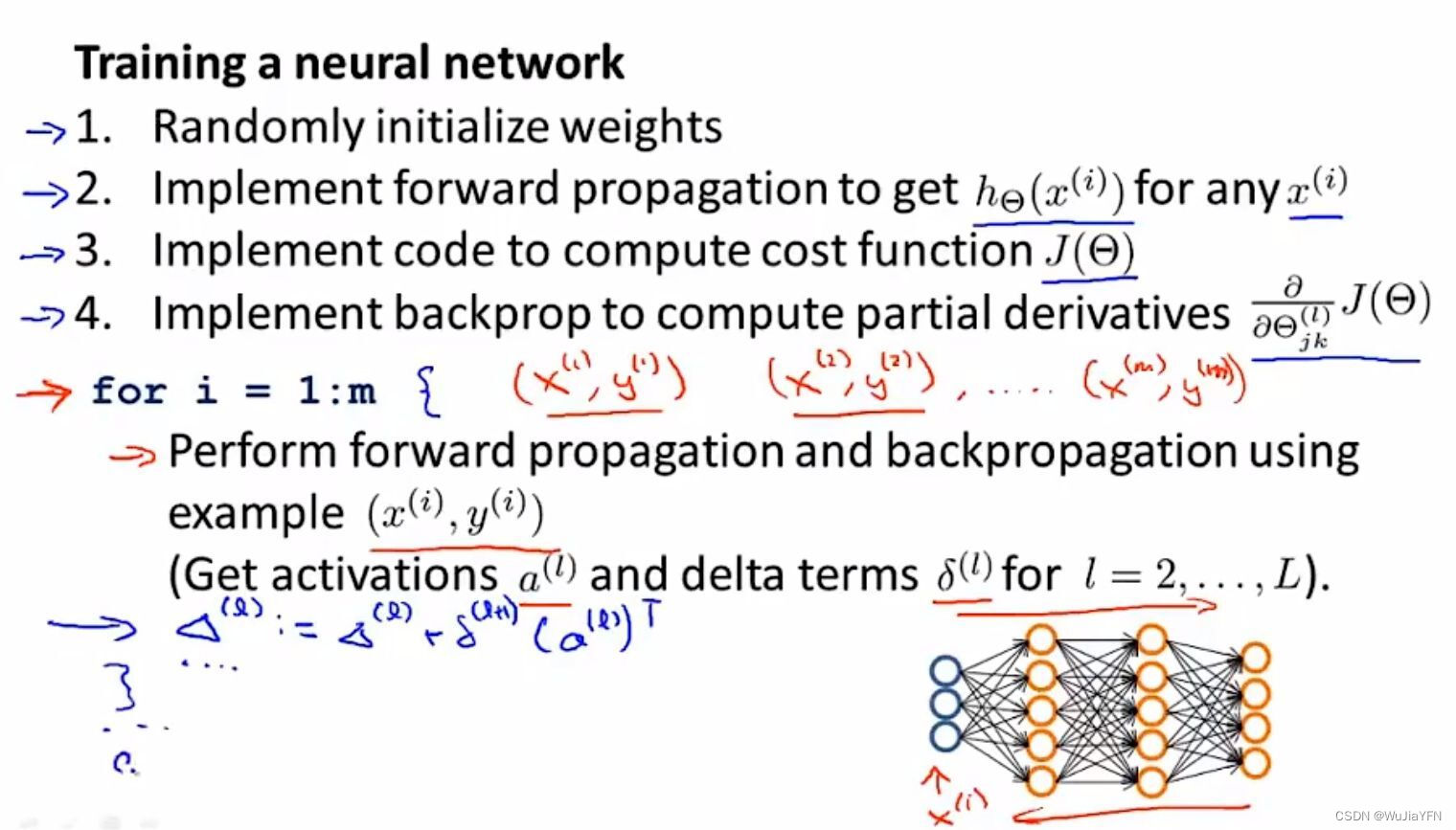
3.2 训练一个神经网络的基本步骤

1. 随机初始化权重矩阵initialization weights

   • 通常把权重初始化为很小的值，接近于0

2. 执行前向传播算法计算预测值forward propagation

   • 即对于神经网络中任意一个输入 x^(i) 计算出对于的 h(x^(i) )的值，也就是一个输出值 y 的向量

3. 通过代码计算出代价函数J(θ)

4. 执行反向传播算法来计算出偏导数项，即dJ/dθ

   • 具体实现过程：使用for 循环对m 个样本进行遍历，在循环内对每个样本进行前向和反向算法
   • 得到神经网络每一层中每个单元的激活值和 delta 项
   • 在循环体外通过 delta 计算出偏导数项

   

5. 梯度检验gradient check

   • 把用反向传播算法得到的偏导数值与用数值方法得到的估计值进行比较
   • 用梯度检测来确保两种方法得到基本接近的两个值，确保用反向传播算法得到的结果时正确的
   • 停用梯度检测

6. 使用一个最优化算法（如梯度下降算法或者更加高级的优化算法）和反向传播算法相结合，来得到最小化 J(θ)

   • J(θ) 是一个非凸函数，理论上可能得到的是局部最小值

   

如果觉得文章不错的话，可以给我点赞鼓励一下哦，欢迎收藏文章
关注我，我们一起学习，一起进步！！！