第3部分，应该可以开始介入，概率的相关概念了。

从前面的，实验，事件，计数等各个概念的引入，，现在可以引导到 概率 的概念了

1 什么是概率，为什么要研究概率？

1.1 问题走到概率这的一个简短逻辑

• 前面确定了，实验时，可能发生的各种事件
• 而各种事件，可以数字化为，各种对应的随机变量
• 然后，对事件/随机变量，可以进行计数 counting，计数后就得到了 样本空间内的所有样本点（当然，很多实验无法得到全部样本点）
• 得到事件，和事件的次数了，接下来可以干嘛？ 继续分析啊---比如占比分析
• 而 事件的数量的比例分析，就是概率了

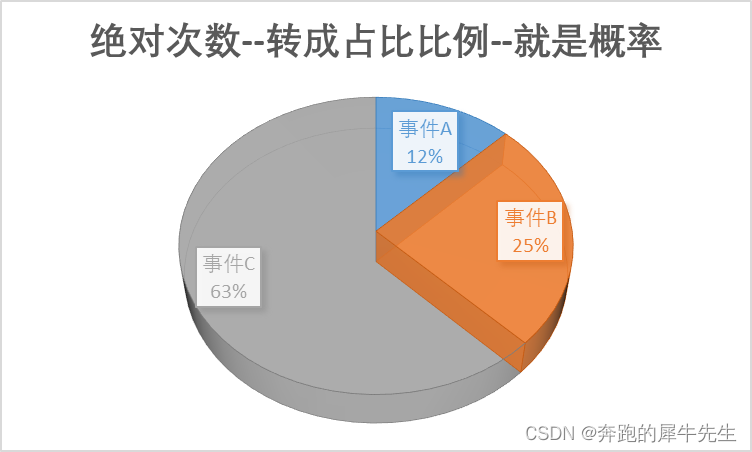
1.2 本篇的思维导图

1.3 原始本地笔记

2 分析概率的方法有哪些种？

2.1 概率分配的两种方法                

• 后验，统计得来 ：
• 相对频次法, 通过大量实验，用频次算频率，频率模拟概率
• 先验，计算构成分析出
• 事件的概率，先界定事件包含哪些 样本点，然后算这些概率之和作为这个事件的概率
• 比如有种特殊情况，就是先验概率的一种 ：等概率模型，p=1/n

3 概率的基本概念

3.1 概率和边缘概率

• 概率            probablity                          
• 边缘概率     Marginal probability 
• 如果是2个概率的联合概率，边缘概率就等于概率把

3.2 联合概率（同时发生的概率）

• 联合概率     joint probability            P(AB)
•     两个事件，同时发生的概率            
•     P(AB)             
•     P(A ∩ B) = P(B)P(A | B) = P(A)P(B | A)     

3.2.1 联合概率的概念

• 联合概率，也就是同时发生
• 对应就是事件相交，因此，联合概率也可以认为就是相交的概率

• 相交      =不互斥     =可以同时发生
• 不相交   =互斥        =不可以同时发生

3.3 条件概率

• 条件概率     Conditional probability            
• P(B | A) =P(AB) / P(A) 
• 条件概率等于，两者同时发生概率/ 先发生事件的概率

• 情况1： 发生其他事件B后，事件A发生的概率 （分母不是全部样本空间，而是只发生了B的样本空间）            
•  情况2： 发生其他事件B后，修改A的先验概率                   

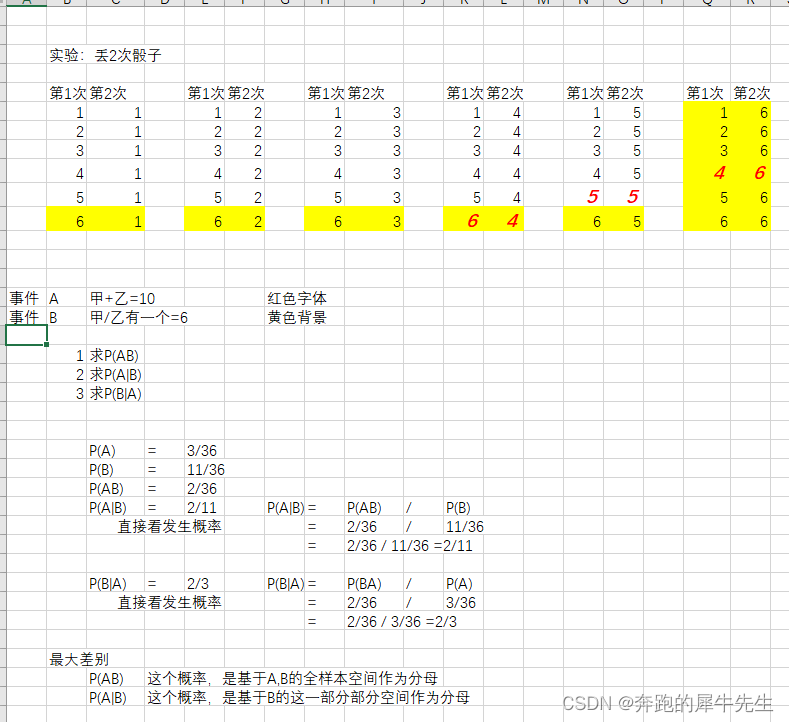
3.4 例题，比较联合概率和条件概率

3.4.1 联合概率和条件概率不同

• 联合概率：两者同时发生的概率（都还未发生！）
• 条件概率，一个事件已发生，求另外一个事件此时发生的概率
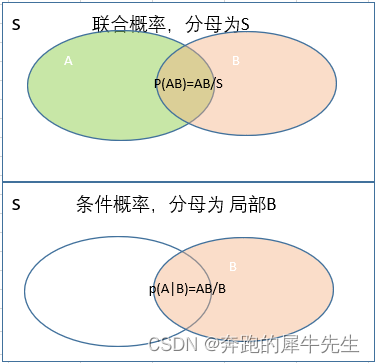
• 联合概率，还是以全部样本空间作为分母
• 条件概率，是以，已经发生的事件的 部分概率，作为分母的！！

4 离散型和连续型的概率

4.1 离散型---概率分布函数

• 离散型随机变量的概率分布，概率分布函数，Probability mass function，PMF
• 离散型随机变量，只有分布，散的分布，没有密度
• 这个函数的定义域 domain 是随机变量的所有可能取值
• 对于任意一个取值来说，0 ≤ P(xi) ≤ 1
• 对于所有取值来说，ΣP(xi) = 1
   

4.2 连续型---概率密度函数

• 连续性随机变量的概率分布，概率密度函数，Probability density function，PDF
• 只有在实数区域上连续的 连续变量，才有密度之说法
• 对于任意一个取值来说，0 ≤ P(xi) ，注意这里不需要 ≤ 1，并且在实际应用中，连续型随机变量取得任意一个具体数值的概率都为 0
• ∫ p(x)dx = 1

5 高级的概率概念

5.1 PMF

• PMF : 概率质量函数 / 概率分布函数（probability mass function), 概率质量函数是离散随机变量在各特定取值上的概率。
• 常见的连续随机变量分布的PDF函数：均匀分布，指数分布，Gamma分布和正态分布等。
• 简单的说
• 可以是个if,
• 也可以说是个分段函数

  

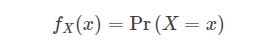
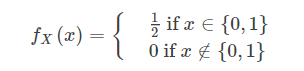
5.2 PDF

• PDF：概率密度函数（probability density function）, 连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。
• 常见的离散随机变量分布的PMF函数：伯努利分布，二项分布，泊松分布。
• 简单的说，就是一个积分

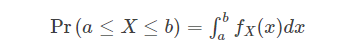
5.3 CDF

• CDF分布函数，累计分布函数
• 重点是：累计的
• 离散的，连续的变量都有分布函数
• CDF : 累积分布函数 (cumulative distribution function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布

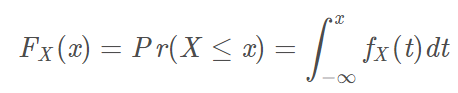
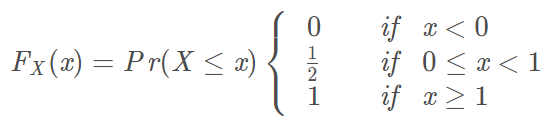
6 曾经有哪些经典的概率分析模型

• 可以认为是历史模型
• 也可以认为是经典的简化模型
• 也可以认为是解决一类问题很好用的实用模型

6.1具体的概率模型

• 古典概型，等可能概型
• 贝努利实验，只有2种结果
• 等等，未完成