-
矩阵分析与应用-13-矩阵的迹
矩阵的迹
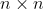 矩阵
矩阵 的对角元素之和称为
的对角元素之和称为 的迹(trace)(注:非正方矩阵无迹的定义),记作
的迹(trace)(注:非正方矩阵无迹的定义),记作 ,即
,即
例如矩阵:

其迹为:

下面是矩阵的迹满足的等式、不等式关系与一些性质。
关于迹的等式
()若A和B均为n×n矩阵,则tr(.A土B)= tr(A)±tr(B)。
(2)若c是一个复或者实的常数,则 tr(cA) = ctr(A)。
(3)若A和B均为n×n矩阵,并且
 和
和  。为常数,则
。为常数,则 。
。(4)矩阵A的转置、复数共辄和复共瓴转置的迹分别为

![tr(A^*)=[tr(A)]^*](https://1000bd.com/contentImg/2022/07/30/050054154.gif)
![tr(A^H)=[tr(A)]^*](https://1000bd.com/contentImg/2022/07/30/050054889.gif)
(5)迹是相似不变量:若A 为m × n矩阵,且B为n x m矩阵,则tr(AB) = tr(BA).
(6)若矩阵A和B均为mx n矩阵,并且非奇异,则

(7)若A是一个m×n矩阵,则
 (零矩阵)。
(零矩阵)。(8)
 和
和  。
。(9)分块矩阵的迹满足

式中,
 ,
, ,
, ,
, 。
。(10)矩阵
 和
和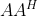 的迹相等,且有
的迹相等,且有
(11)迹等于特征值之和,即

(12)对于任何正整数k,有

式右的和称为A的诸特征值的k次矩。
2.关于迹的不等式
(1)对一个复矩阵
 ,有
,有 。
。(2)若A,B均为m × n 矩阵,则
![tr[(A^TB)^2] \leq tr(A^TA)tr(B^TB)](https://1000bd.com/contentImg/2022/07/30/050110810.gif) (Cauchy-Schwartz不等式)
(Cauchy-Schwartz不等式)![tr[(A^TB)^2] \leq tr(A^TAB^TB)](https://1000bd.com/contentImg/2022/07/30/050111845.gif)
(3) Schur 不等式:
 。
。(4)
![tr[(A+B)(A+B)^T]\leq 2[tr(AA^T)+tr(BB^T)]](https://1000bd.com/contentImg/2022/07/30/050155996.gif) 。
。(5)若A和B为m x m对称矩阵,则
 。
。 -
相关阅读:
css正确的语法
流程自动化
【建议收藏】职场人口头和书面沟通必备词语,瞬间高大上
elmentui表格修改可点击排序元素
通过字符设备驱动分步注册方式编写LED驱动,完成设备文件和设备的绑定
有效的字母异位词(C++解法)
第13篇 2D绘图(三)绘制文字
03 里氏替换原则
攻防千层饼
删除不必要的内核模块
- 原文地址:https://blog.csdn.net/Xiao__fly/article/details/126001740